Размер матрицы все, что нужно знать
Раньше было вполне логичным, что покупая компактную камеру, вы получали небольшую матрицу, а если выбирали крупногабаритную зеркалку со сменными объективами, матрица на ней была значительно больше. Это сказывалось на качестве фотографий, поскольку чем больше матрица, тем более детализированы были изображения.
Сейчас это в принципе, тоже в какой-то мере актуально, матрица — это самая дорогая часть камеры в плане производства, и чем больше матрица, тем и камера, соответственно, дороже. Потому на дорогие камеры обычно не устанавливаются матрицы 1/2.3 дюймовые, а на дешевых, соответственно, не найти полнокадровую.
Но надо сказать, что сейчас многие производители стали предлагать компактные камеры с относительно большими матрицами, точно так же как и камеры под сменные объективы с меньшими матрицами. Так что разобраться в ситуации, пожалуй, стало сложнее. Небольшие матрицы способны отлично срабатывать в различных условиях, и даже имеют некоторые преимущества перед большими.
За последние годы и сама технология создания матриц значительно продвинулась вперед, так что сегодня большое количество предлагаемых вариантов может смутить даже опытного пользователя, что уж говорить о тех, кто приобретает первую фотокамеру. А ведь размер матрицы еще и на фокусном расстоянии сказывается, так что учитывать при выборе камеры действительно нужно очень многое.
Итак, мы решили разобраться в различных типах матриц, чтобы расставить все по местам. Но для начала нужно уточнить, как именно размер матрицы влияет на эффективное фокусное расстояние.
Фокусное расстояние
Итак, мы уже выяснили, что размер матрицы связан с фокусным расстоянием, то есть с тем, какой именно объектив подойдет вашей камере. Если вы приобретаете компактный девайс с не съемным объективом, проблема сама собой отпадает, то есть с позиции покупателя это гораздо проще. Но не просто так профессионалы выбирают именно те камеры, где объективы можно менять. Любой объектив должен иметь поле (круг) изображения или диаметр света, который существует в объективе и который покрывает размер матрицы.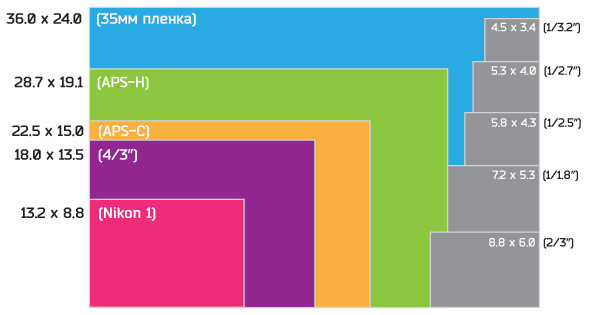
Итак, встроенные или нет, объективы всегда помечены реальным фокусным расстоянием, а не эффективным фокусным расстоянием, которое вы получите при использовании на той или иной камере. Но проблема в том, что различные объективы с различной маркировкой могут в итоге обеспечить одно и то же фокусное расстояние для работы. Почему? Потому что они предназначены для разных матриц. Именно поэтому производители помимо маркировки указывают эквивалент, где основным расстоянием считается 35мм или полнокадровая матрица.
Вот — один из примеров: камера с матрицей меньше чем полнокадровая вполне может использоваться с 18-55мм объективом, но на деле фокусное расстояние, которое вы получите будет ближе к 27-82мм. Это все происходит потому, что матрица не достаточно велика, чтобы использовать объектив точно так же как смог бы полнокадровый. Из-за того, что периферическое пространство внутри объектива не принимается в расчет, получается тот же эффект как от использования объектива с большим фокусным расстоянием.
В компактных камерах может был установлен 19мм объектив, но из-за размера матрицы, который меньше фуллфрейма, вы получите в итоге большее фокусное расстояние, около 28мм. Точная длина определяется кроп-фактором, то есть числом, на которое нужно увеличить данное под фуллфрейм фокусное расстояние, чтобы выяснить какое расстояние получится на той или иной камере.
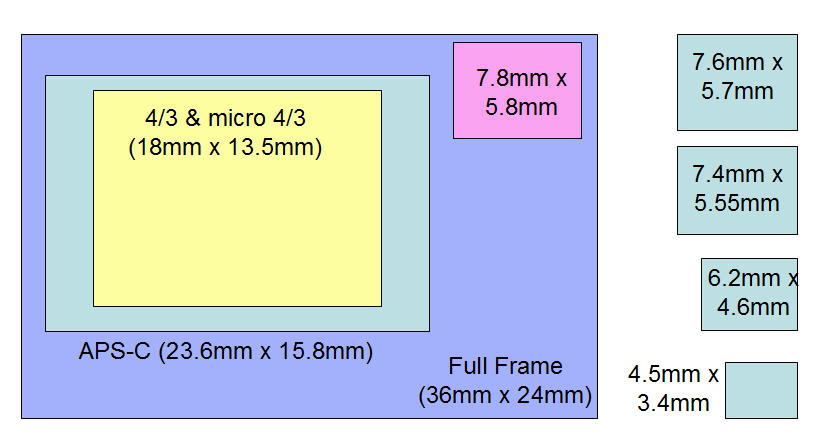
Размеры матриц
1/2.3 дюйма
Размер такой матрицы примерно 6.3 x 4.7 мм. Это — самая маленькая матрица, которую можно найти в современных камерах, и чаще всего — в бюджетных компактных моделях. Разрешение такой матрицы составляет, как правило, 16-20 Мп.
По крайней мере такой расклад был самым популярным какое-то время назад. Сегодня многие производители стали делать больший упор на любительские фотоаппараты с большими матрицами, так что и размер такой не так распространен как ранее.
Однако, преимущество в том, что такой размер позволяет получить компактную камеру и использовать ее с длиннофокусными объективами, например компактными суперзумами.
При хорошем освещении такие камеры могут предоставить неплохой результат, но для более придирчивых фотографов они точно не подойдут, поскольку при низкой освещенности будут зернить.
1/1.7 дюймов
Размер этих матриц 7.6 x 5.7мм. С такой матрицей гораздо проще выделить объект съемки из фона, и соответственно, производительность в плане деталей как в тени, так и на свету. Так что использовать их можно уже в более разнообразных условиях. Раньше такие камеры были самыми распространенными среди любителей, но сейчас их место стремительно занимают дюймовые матрицы, о которых речь и пойдет дальше.
А вот 1/1.7 дюймовые матрицы используются в некоторых относительно устаревших камерах Q-серии Pentax.
Дюймовые матрицы
Размер дюймовой матрицы 13.2мм x 8.8мм. Сегодня такие матрицы очень популярны на различных типах камер, размер позволяет им оставаться легкими и компактными. Логично, что самый популярный способ применения для дюймовой матрицы — это карманные любительские камеры, на которых объектив будет лимитирован 24-70мм или 24-100мм (если брать эквивалент 35мм). Однако, на некоторых суперзум камерах он тоже используется?, примеры — это Sony RX10 III и Panasonic FZ2000.
Логично, что самый популярный способ применения для дюймовой матрицы — это карманные любительские камеры, на которых объектив будет лимитирован 24-70мм или 24-100мм (если брать эквивалент 35мм). Однако, на некоторых суперзум камерах он тоже используется?, примеры — это Sony RX10 III и Panasonic FZ2000.
Гораздо лучше дюймовая матрица нам знакома по камерам Nikon серии 1, например Nikon 1 J5 — отличной и легкой камере, которая способна делать отличные фото и снимать 4К видео. Такую матрицу можно встретить даже среди смартфонов — Panasonic CM1.
Камеры с дюймовой матрицей способны показать результаты, значительно отличные от предыдущих вариантов. Качество их будет высоким, а даже компактные камеры, как правило, имеют широкую максимальную апертуру, так что на матрицу попадает достаточно света, потому и фотографии выходят четкими и резкими.
Частично, это результат технологии, а не только размера матрицы. Матрицы современного производства могут более эффективно захватывать свет.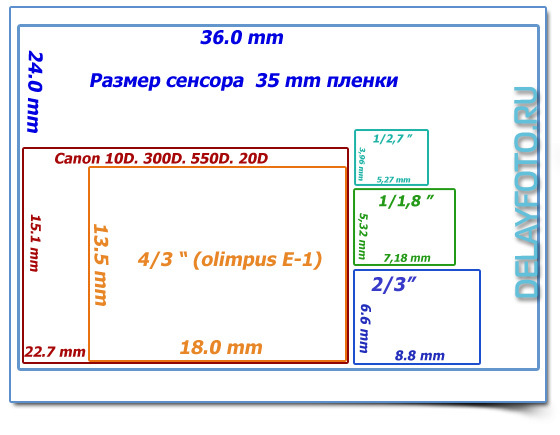
Микро 4/3
Матрица микро 4/3 имеет физический размер 17.3 x 13мм. Этот формат используется в компактных зеркалках и беззеркалках Olympus и Panasonic. Они ненамного больше по размеру, чем дюймовые матрицы, но меньше чем APS-C, речь о которых пойдет ниже.
По сути, микро 4/3 — это четверть размера полнокадровой матрицы, так что считать для нее активное фокусное расстояние предельно просто: достаточно умножить фокусное расстояние на 2.
Иными словами, 17мм объектив на камере с матрицей микро 4/3 обеспечит фокусное расстояние такое же, как 34мм объектив на полнокадровой матрице. По аналогии, 12-35мм даст 24-70мм и так далее.
На камере Lumix DMC-LX100 используется матрица микро 4/3 разрешением 12.8 Мп. Это — одна из компактных цифровых камер, которые обладают большим количеством функций и небольшим размером. Камера оснащена объективом Leica с фокусным расстоянием 24-75мм.
APS-C
Средний физический размер такой матрицы 23. 5 x 15.6мм. Такая матрица используется на зеркальных камерах для начинающих и любительских камерах, а сейчас и на многих беззеркалках. Матрица APS-C обеспечивает отличный баланс между качеством изображения, размером и вариативностью в плане совместимости с различными объективами.
5 x 15.6мм. Такая матрица используется на зеркальных камерах для начинающих и любительских камерах, а сейчас и на многих беззеркалках. Матрица APS-C обеспечивает отличный баланс между качеством изображения, размером и вариативностью в плане совместимости с различными объективами.
Не все APS-C матрицы одинаковы по размеру, ведь это зависит от производителя тоже. Например, матрицы APS-C на камерах Canon физически немного меньше чем те, что установлены в Nikon и Sony, таким образом ее кроп-фактор равен 1.6x, а не 1.5x. В любом случае, APS-C — это всегда отличный вариант и профессиональные фотографы нередко предпочитают его для съемок природы и спортивных мероприятий, потому что благодаря кроп-фактору появляется возможность “приблизиться” к объекту съемки имеющимся объективом.
APS-C доступны на некоторых компактных камерах, например Fujifilm X100F, это обеспечивает высокое качество для фотографий на портативных камерах, особенно в комплекте с объективами с постоянным фокусным расстоянием.
APS-H
Размер матриц APS-H как правило равен 26.6 x 17.9мм. Сегодня этот формат практически не встречается, и ассоциируется только с устаревшими моделями Canon EOS-1D (EOS-1D Mark III и Mark IV). Сейчас, правда, в этой серии используются фуллфреймы.
Поскольку APS-H больше чем APS-C, но меньше полнокадровой матрицы, кроп-фактор, соответственно равен 1.3х, потому 24мм объектив обеспечит на такой камере фокусное расстояние приблизительно 31мм.
Одна из последних фотокамер, где можно встретить такую матрицу — это Sigma sd Quattro H. Однако и Canon решили не отказываться от APS-H совсем, и предпочли применить эту матрицу для камер наблюдения, а не для зеркальных фотоаппаратов.
Фуллфрейм
36 x 24мм она же фуллфрейм, она же полнокадровая матрица и она же примерно такая же по размеру как негатив пленочной фотографии. Используются полнокадровые матрицы на любительских и профессиональных камерах и считаются самым удобным вариантом для съемок. Размер такой матрицы позволяет ей принимать на себя больше света, вследствие чего и фото получаются выше по качеству чем с меньшими матрицами. Соответственно, и когда речь идет о количестве пикселей, выбор больше. А разрешение полнокадровых матриц варьируется от 12 до 50Мп.
Используются полнокадровые матрицы на любительских и профессиональных камерах и считаются самым удобным вариантом для съемок. Размер такой матрицы позволяет ей принимать на себя больше света, вследствие чего и фото получаются выше по качеству чем с меньшими матрицами. Соответственно, и когда речь идет о количестве пикселей, выбор больше. А разрешение полнокадровых матриц варьируется от 12 до 50Мп.
Кроп-фактор, конечно, в случае с полнокадровой матрицей значения не имеет, так как маркировка объектива будет соответствовать активному фокусному расстоянию. Однако же, некоторые объективы, созданные под APS-C матрицы все равно можно использовать с фуллфреймами, но разрешение будет ограничено (камера обрежет углы, чтобы избежать виньетирования). Но проверять совместимость, разумеется, нужно всегда, иначе есть риск повредить зеркало.
Средняя (медиум) матрица
44мм x 33мм — размер такой матрицы. Это, очевидно, больше фуллфрейма и с момента появления такие матрицы вызвали оживленный интерес и дискуссии. Они использованы в камерах Fujifilm GFX 50S, Hasselblad X1D и Pentax 645Z, последняя немного старше остальных. Применяются они в основном, исключительно профессиональными фотографами в силу цены таких камер и их специфики.
Они использованы в камерах Fujifilm GFX 50S, Hasselblad X1D и Pentax 645Z, последняя немного старше остальных. Применяются они в основном, исключительно профессиональными фотографами в силу цены таких камер и их специфики.
Не факт, что на этом развитие матриц как таковых остановится, но пока что это — все доступные на рынке типы матриц, а какая подойдет для ваших фото интересов, решать только вам.
Что важнее размер матрицы фотоаппарата или количество мегапикселей?
Физический размер матрицы фотоаппарата, мегапиксели и качество снимков
По мере развития цифровой фото и видеотехники число мегапикселей, которыми производители приманивают покупателей, становится все больше. Но мало кто знает, что на самом деле для получения качественных фотографий гораздо важнее не разрешение, а физический размер самой матрицы.
Давайте разберем понятие мегапиксели. Пиксель — это одна маленькая точка из миллиона других, из которых состоит изображение.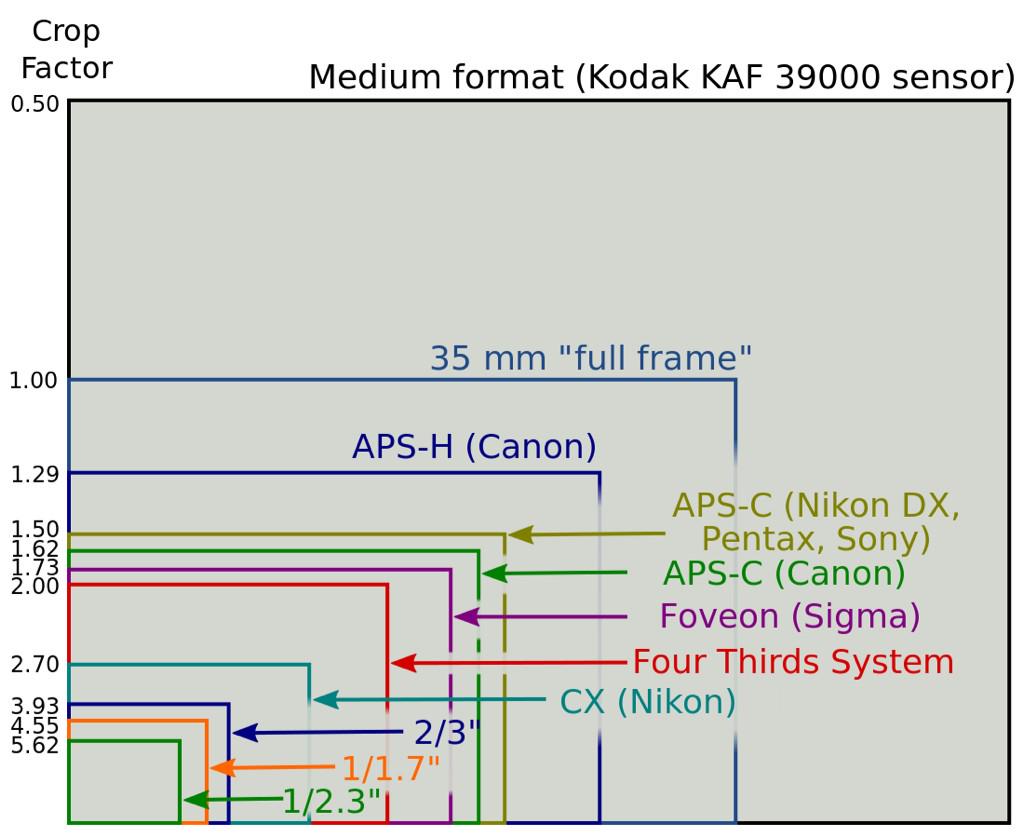
Эти точки разные по размеру. Применительно к цифровой матрице, каждый пиксель — это миниатюрный датчик, на который при фотосъемке попадает свет, затем он преобразуется в цифровой сигнал и в таком виде передается в компьютер фотоаппарата. Таких датчиков на матрице огромное количество. Чем больше размер самой матрицы, тем больше размер каждого пикселя и их общее количество. Поэтому зависимость между матрицей и качеством снимков – самая прямая.
Вроде бы логично было бы писать эту площадь в виде длины и ширины, и желательно в миллиметрах. Но поскольку почти все параметры цифровой техники пришли к нам из-за границы, принято указывать размер матрицы в так называемых обратных дюймах, т.е. дробью, где в числителе единица, а в знаменателе – дюймовый размер матрицы. Например: 1/3.2 , 1/2.7 и т.д.
Большинству покупателей эти цифры мало о чем говорят.
Как правило, чем дешевле камера, тем меньше у нее физический размер матрицы и тем хуже качество сделанных ею фотографий.
Среди дорогих компактных камер иногда можно встретить модели с матрицей 2/3 , что обеспечивает неплохую детализацию снимков и достаточно высокую светочувствительность.
Матрицы 1/5 или 1/6 мы найдем в большинстве бюджетных зеркальных камер, это примерно половина кадра пленки 35 мм. Во многом именно за счет размера матрицы фотографии, сделанные зеркалкой, обычно выгодно отличаются от тех, которые сняты компактами.
Есть еще полнокадровые матрицы (36х24 мм), которые по размеру соответствуют полному кадру 35 мм, и матрицы среднего формата (60х45 мм), которые больше этого стандартного кадра и применяются в дорогих зеркальных камерах.
Итак, на что же, собственно, влияет размер матрицы?
Первое – на размер и вес самой камеры. Фотоаппараты с небольшими матрицами компактны, их можно носить в кармане.
Камеры с большими матрицами, например, средний формат, приходится таскать в специальных кофрах, а то и вовсе использовать только в студии.
Второе – на увеличение цифрового шума — или, как еще по старинке говорят, зерна — на ваших снимках. «Шумные» фотографии выглядят так, будто изображение разбито на множество заметных цветных точек. Вид у них неопрятный, грязноватый.
Появление шума обусловлено тем, что на большую по площади матрицу попадает больше света, чем на маленькую. В результате передаваемый ею полезный сигнал будет лучшего качества, а отсюда – и лучшая проработка деталей, и более качественная цветопередача, и большая яркость картинки.
Кроме того, датчики большой матрицы расположены дальше друг от друга и изоляция между ними лучше, поэтому меньше пробивающих эту изоляцию токов, которые создают помехи, ухудшающие качество фотографий.
Отсюда, кстати, следует, что большое разрешение (те самые большие мегапиксели) при маленьком размере матрицы – скорее вредно, чем полезно.
Что будет, если на матрицу одного размера впихнуть 8 000 000 пикселей и 12 000 000? Во втором случае это приведет к уменьшению размера датчиков, ухудшению слоя изоляции между ними — и увеличению цифрового шума.
От разрешения матрицы в мегапикселях зависит то, какого размера снимки вы сможете напечатать без заметной потери качества. Разрешения 8 мегапикселей достаточно для печати фотографий формата А4 (альбомный лист). И при малом размере матрицы такое разрешение еще не приводит к заметному цифровому шуму.
Выбирая себе фотоаппарат, обязательно обращайте внимание на физический размер матрицы, желательно чтобы он был максимально большим, насколько вы сможете себе позволить по финансам. От этого напрямую зависит качество сделанных фотографий, конечно если вы выберите зеркальную камеру, советую вам не покупать стандартный «китовый» объектив, который предлагают чаще всего в комплекте. Так как оптически он очень слабый и не надежный.
Так как оптически он очень слабый и не надежный.
Но будьте готовы, что зеркальная камера с хорошим объективом будет стоить дороже компактного фотоаппарата да и будет не совсем миниатюрной.
Так что смотрите сами, что для вас важнее. Любые вопросы по фототехнике вы можете смело задать нашим фотографам:
+375-29-122-92-40 (Viber)
+375-29-122-92-40 (whatsApp)
E-mail: [email protected]
Skype: sigma-by
Пишите в чат фотографу!
К вопросу о выборе объектива
Планируя развернуть систему видеонаблюдения, вы неизбежно задаетесь вопросами: куда и сколько установить камер? Как определить наилучшие места их расположения, чтобы избежать «слепых зон»? На каком расстоянии от объектов наблюдения установить камеры, чтобы в итоге получилось достаточно четкое изображение нужных деталей?
На вид и качество изображения большое влияние оказывают не только параметры видеокамеры и объектива, но и их правильное сочетание. Так, иногда отличный, дорогой объектив может давать даже худшее изображение, чем альтернативная дешевая модель.
Так, иногда отличный, дорогой объектив может давать даже худшее изображение, чем альтернативная дешевая модель.
Расскажем об основных факторах, влияющих на качество и масштаб видеоизображения, которые следует учитывать при выборе объектива для камеры, чтобы по максимуму использовать их возможности и при этом избежать ненужных затрат.
Угол обзора объектива
Одной из важных характеристик систем видеонаблюдения является угол обзора объектива. От него напрямую зависит количество и возможные места установки камер на объекте. Угол обзора объектива определяет величину видимого объекта и масштаб изображения в кадре.
Из этой схемы видно, что на величину угла обзора напрямую влияет не только фокусное расстояние объектива, но и размеры матрицы:
И если с фокусное расстояние определить довольно легко, зная модель объектива, то с размером матриц не все так просто.
Размер матрицы видеокамеры
В зависимости от соотношения сторон (4:3 или 16:9), у матриц с одной и той же диагональю физические размеры различны (Таблица 1). Поэтому, например, камера на матрице 1/3’’ с соотношением сторон 4:3 дает больший угол обзора по вертикали и меньший по горизонтали, чем камера на матрице с такой же диагональю, но соотношением 16:9.
| Формат матрицы | Диагональ матрицы (мм) | Соотношение сторон | |||
| 4:3 | 16:9 | ||||
| Ширина (мм) | Высота (мм) | Ширина (мм) | Высота (мм) | ||
| 1/4 | 4. 23 23 | 3.39 | 2.54 | 3.69 | 2.08 |
| 1/3 | 5.64 | 4.52 | 3.39 | 4.92 | 2.77 |
| 1/2.8 | 6.05 | 4.84 | 3.63 | 5.27 | 2.96 |
| 1/2.7 | 6.27 | 5.02 | 3.76 | 5.47 | 3. 07 07 |
| 1/2.5 | 6.77 | 5.42 | 4.06 | 5.90 | 3.32 |
| 1/2 | 8.47 | 6.77 | 5.08 | 7.38 | 4.15 |
В целях облегчения подбора совместимой оптики и расчета углов обзора обычно заявляют ближайшее из стандартных значений для диагонали матрицы: 1’’, 1/2’’, 1/2.5’’, 1/2.7’’, 1/2.8’’, 1/3’’, 1/4’’. При этом измерять ее принято в видиконовых дюймах. Эта единица измерения, равная 2/3 обычного дюйма, была введена со времен зарождения телевидения, когда приёмным элементом в телекамере служила электронная трубка («видикон»), а размер обозначал её диаметр (в который должен был вписываться с запасом снимаемый кадр).
Помимо этого необходимо помнить, что на некоторых режимах работы камеры часть пикселей матрицы не используется. Поэтому при определении угла обзора следует говорить не столько о размере матрицы, сколько о размере активной области матрицы.
Для наглядности приведем несколько примеров:
N1000 (Рис. 2): для всех возможных режимов работы активная область матрицы остается неизменной.
Рис. 2 N1000. 0.3 Мп, VGA, 1/4’’Размер матрицы: 3.7 х 2.77мм, диагональ 4,62 мм=1/3.67 видиконовых дюйма (ближайшее значение 1/4’’).
N37210 (Рис. 3): в зависимости от режима работы активная область матрицы изменяется почти на 30% по вертикали и 25% по горизонтали.
Рис. 3 N37210. 2 Мп, FullHD, 1/2.7’’Размер матрицы: 5.71 х 3.14 мм, диагональ 6.52 мм=1/2.6 видиконовых дюйма (ближайшее значение 1/2.7’’). При разрешении 1024х768 размер активной области матрицы уменьшается до 4.58 х 2.32 мм.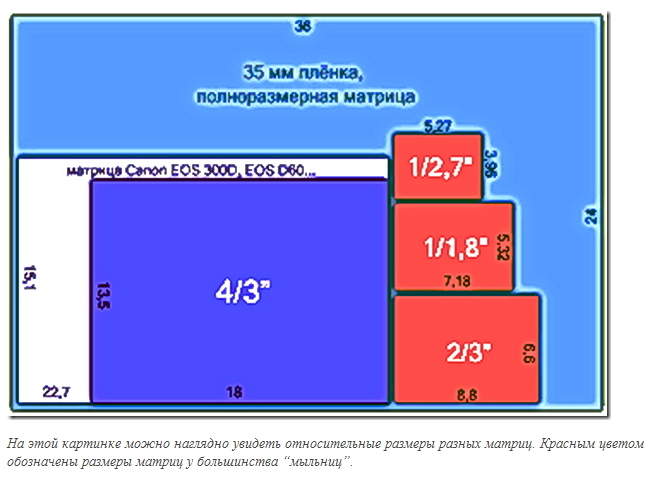
BD2570 (Рис. 4): в зависимости от режима работы активная область матрицы изменяется почти на 50% по вертикали и 25% по горизонтали.
Рис. 4 BD2570. 5 Мп, 1/2.5’’Размер матрицы: 5.61 х 4.31 мм, диагональ 7.08 мм=1/2.39 видиконовых дюйма (ближайшее значение 1/2.5’’). При разрешении 1280х720 размер активной области матрицы уменьшается до 4.22 х 2.21 мм.
Из этих примеров видно, что величина матрицы может отличаться от указанной в паспорте, а размер ее активной области — меняться в зависимости от режима работы.
Однако, при вычислении угла обзора следует учитывать не только эту особенность, но и тот факт, что аберрации реального объектива приводят к усложнению расчетов.
В большинстве объективов, используемых в CCTV, повышение качества изображения осуществляется путем усложнением оптической системы с целью уменьшения аберраций, влияющих на разрешающую способность. Это часто приводит к увеличению геометрических аберраций, таких как дисторсия (рис. 5), воспринимаемых как побочный эффект.
5), воспринимаемых как побочный эффект.
Например, положительная дисторсия сокращает угол обзора непропорционально быстро при уменьшении активной области матрицы (синяя рамка на рис. 6).
Рис. 6 Кадры, сделанные объективом с дисторсией (а) и объективом без дисторсии (б)Этот эффект наблюдается как при смене режимов работы одной и той же камеры, так и при установке объектива на матрицы разных форматов. Например, видимый угол обзора у 8-мм дисторзирующего объектива на матрице 1/2 может быть как у 6-мм, а на матрице 1/3 — как у 7-мм.
Непропорциональное уменьшение угла обзора реального объектива с положительной дисторсией объясняется смещением фокальной плоскости в центре кадра, в отличие от идеального объектива (рис. 7), для которого верны соотношения
Рис. 7 Оптическая схема идеального объектива (а) и реального объектива с положительной дисторсией (б)
7 Оптическая схема идеального объектива (а) и реального объектива с положительной дисторсией (б)Таким образом, спрогнозировать, какими будут качество и масштаб видеоизображения для пары «камера-объектив» можно достаточно точно только если учитывать все влияющие на это параметры видеосистемы. Универсальный калькулятор BEWARD позволяет не просто вычислить области видимости и углы обзора, но и подобрать подходящие объективы для камер BEWARD.
О матрицах простым языком, Гл. 1, Или опять про мегапиксели
Для начала, дадим определение матрице. Матрица — это светочувствительный сенсор преобразующий спроецированное на него через объектив оптическое изображение в электрический сигнал (цифровой аналог фотопленки), который затем с помощью других микросхем фотокамеры преобразуется в поток цифровых данных, который можно записать в файл поместить на носитель информации (карту памяти), а затем посмотреть на мониторе либо распечатать на фотобумаге.
Наверное не одну сотню раз вы слышали, что чем больше в матрице мегапикселей, тем качественней и детализированней будут снимки. Это самое большое заблуждение. Не количество мегапикселей в матрице влияет на картинку, а ее физический размер.
Это самое большое заблуждение. Не количество мегапикселей в матрице влияет на картинку, а ее физический размер.
И раз уж обещал обо все рассказывать простым языком и, что у нас на сайте не будет рутинной теории, то расскажу пожалуй на “пальцах”.
Взгляните на эту картинку, здесь схематично представлены матрицы, вернее их физические размеры, каждому цвету соответствует определенный размер матрицы. А ниже будут приведены модели фотокамер с сопоставлением физического размера ИХ матрицы и количеством мегапикселей “затолканным” в нее. Итак, приступим.
На этой картинке видно, как разительно отличаются матрицы по своему размеру. (между прочим прошу обратить ваше внимание на то, что масштаб здесь увеличен).
1) Начнем как полагается с цифры 1. Красным цветом выделена матрица «стандартной» цифровой компактной камеры, ее диагональ измеряется в дюймах и равна 1/2,3″. Такой матрицей снабжено огромное кол-во компакт камер. Для примера я взял популярные на данный момент цифрокомпакты от Canon, а теперь посмотрите на физический размер их матриц и на кол-во «впиханных» в них мегапикселей. … Есть над чем поразмыслить?
… Есть над чем поразмыслить?
|
СANON Digital IXUS 100 IS Размер матрицы — 1/2,3″ Число Мпикселей — 12,1
|
||
|
СANON Digital IXUS 990 IS Размер матрицы — 1/2,3″ Число Мпикселей — 12,1 |
||
|
СANON Digital IXUS 85 IS Размер матрицы — 1/2,3″ Число Мпикселей — 10 |
||
|
СANON PowerShot SX1 IS Размер матрицы — 1/2,3″ Число Мпикселей — 12,1 |
||
|
СANON PowerShot A480 Размер матрицы — 1/2,3″ Число Мпикселей — 10 |
||
|
СANON PowerShot SX200 IS Размер матрицы — 1/2,3″ Число Мпикселей — 12 |
||
|
Olympus -SP-565 UZ Размер матрицы — 4/3″ Число Мпикселей — 12 |
2) Под цифрой 2 показана матрица размером 4/3 дюйма.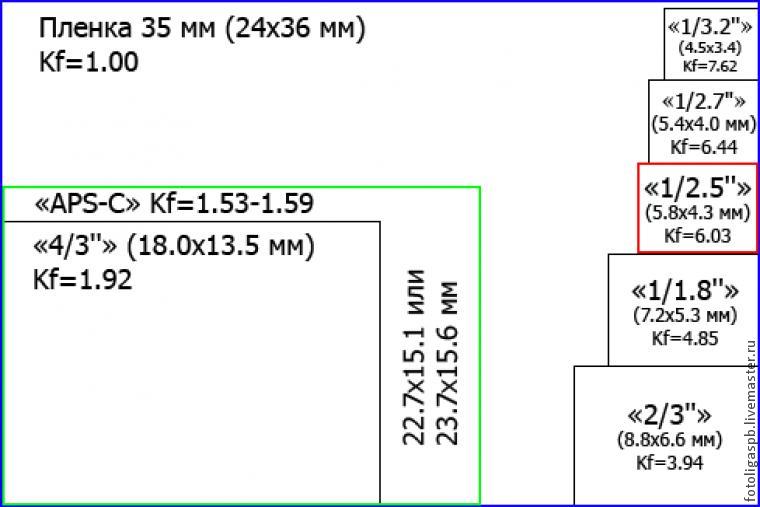 В основном матрицы такого размера ставит на свои камеры компания Olympus.
В основном матрицы такого размера ставит на свои камеры компания Olympus.
Ниже представлены яркие представители семейства Olympus обладающими такими матрицами
|
Olympus — E-410 Размер матрицы — 4/3″ Число Мпикселей — 10
|
||
|
Olympus -E-P1 Размер матрицы — 4/3″ Число Мпикселей — 13.1
|
||
|
||||
3) Под цифрой 3 показана матрица формата APS-C, матрицы этого размера можно встретить на всех популярных моделях цифровых зеркальных фотокамерах начального уровня (т. е. любительских) от Canon и Nikon. Давайте немного углубимся в терминологию. Наверняка вы не раз встречали аббривеатуру DSLR (в интернет или бумажных обзорах по зеркальным фотокамерам). DSLR — (Digital single-lens reflex camera), что означает — Цифровая однообъективная зеркальная камера (однообективная — вовсе не означает, что камера может использует всего один объектив, а означает это что камера не может использовать более одного объектива одновременно; т.е за раз более одного объектива не нацепить)
е. любительских) от Canon и Nikon. Давайте немного углубимся в терминологию. Наверняка вы не раз встречали аббривеатуру DSLR (в интернет или бумажных обзорах по зеркальным фотокамерам). DSLR — (Digital single-lens reflex camera), что означает — Цифровая однообъективная зеркальная камера (однообективная — вовсе не означает, что камера может использует всего один объектив, а означает это что камера не может использовать более одного объектива одновременно; т.е за раз более одного объектива не нацепить)
|
Canon — EOS 1000D Формат матрицы — APS-C Размер матрицы — 22,2 x 14,8 мм Число Мегапикселей — 10,1
|
||
|
Canon — EOS 500D Формат матрицы — APS-C Размер матрицы — 22,3 x 14,9 мм Число Мегапикселей — 15 |
||
|
Canon — EOS 50D Формат матрицы — APS-C Размер матрицы — 22,3 x 14,9 мм Число Мегапикселей — 15,1 |
||
|
Nikon — D60 Формат матрицы — APS-C Размер матрицы — 23,6×15,8 мм Число Мегапикселей — 10,1 |
||
|
Nikon — D5000 Формат матрицы — APS-C Размер матрицы — 23,6×15,8 мм Число Мегапикселей — 12,9 |
||
|
Sony — A700P Формат матрицы — APS-C Размер матрицы — 23,5×15,6 мм Число Мегапикселей — 12,2 |
||
|
Sony — A350K Формат матрицы — APS-C Размер матрицы — 23,5 x 15,7 мм Число Мегапикселей — 14,2 |
||
|
Pentax K-x Формат матрицы — APS-C Размер матрицы — 23,6 х 15,8 мм Число Мегапикселей — 12,4 |
||
|
Pentax K7 Формат матрицы — APS-C Размер матрицы — 23,4 х 15,6 мм Число Мегапикселей — 14,6 |
Если вы внимательно рассмотрели таблицу, то у вас наверняка появились вопросы: почему формат один (APS-C), а размеры в миллиметрах разные, да и что это вообще за формат? Отвечаю: размеры данного формата могут варьироваться от 20.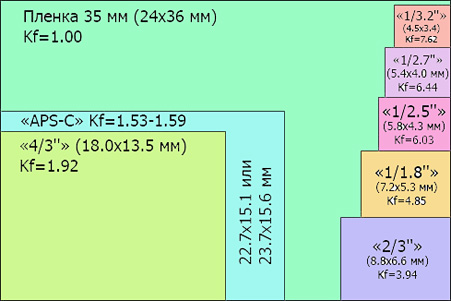 7?13.8 мм до 25,1?16,7 мм. APS-C — Advanced Photo System type-C, что означает Усовершенственная фотосистема классического типа.
7?13.8 мм до 25,1?16,7 мм. APS-C — Advanced Photo System type-C, что означает Усовершенственная фотосистема классического типа.
4) И наконец перейдем к цифре 4. Эта матрица имеет размер 36х24 мм, и равняется по размеру с кадром 35 мм пленки, да, да той пленки на которую вы когда то снимали своими мыльницами от Kodak или Minolta. Матрицу такого размера имеют профессиональные DSLR камеры (это я вас потихоньку приучаю вас привыкать к аббревиатурам), их еще называют полнокадровые или фул фрейм (от full frame) матрицы. Давайте посмотрим на некоторых «монстров», которые имеют их.
|
Canon — EOS 5D Размер матрицы — 36 x 24 мм Число Мегапикселей — 12,8
|
||
|
Canon — EOS 5D Mark II Размер матрицы — 36 x 24 мм Число Мегапикселей — 21,1 |
||
|
Canon — EOS-1Ds Mark III Размер матрицы — 36 x 24 мм Число Мегапикселей — 21,1 |
||
|
Nikon — D700 Размер матрицы — 36 x 24 мм Число Мегапикселей — 12,1 |
||
|
Nikon — D3X Размер матрицы — 36 x 24 мм Число Мегапикселей — 24,5 |
||
|
Sony — A900 Размер матрицы — 36 x 24 мм Число Мегапикселей — 24,6 |
Выводы: Увеличение количества пикселей на матрицах маленького размера происходит за счет уменьшения размера этого самого пикселя. А это черевато возникновением таких проблем как «шумы». Если сравнить матрицы фотокамер СANON Digital IXUS 990 IS и скажем Nikon — D700, то вы уведите, что число мегапикселей у них равно, но вот если сравнить размеры их матриц в миллиметрах…., то сразу видно, кто кому даст фору, так что уважаемые читатели не ведитесь на количество пикселей при покупке фотоаппарата, приглядитесь к размеру матрицы и качеству объектива.
А это черевато возникновением таких проблем как «шумы». Если сравнить матрицы фотокамер СANON Digital IXUS 990 IS и скажем Nikon — D700, то вы уведите, что число мегапикселей у них равно, но вот если сравнить размеры их матриц в миллиметрах…., то сразу видно, кто кому даст фору, так что уважаемые читатели не ведитесь на количество пикселей при покупке фотоаппарата, приглядитесь к размеру матрицы и качеству объектива.
размер матрицы фотоаппарата | Мир сквозь призму
Многие уже в курсе того, что нужно знать, выбирая цифровой фотоаппарат.
Сегодня поговорим о таком важном элементе, как матрица фотоаппарата и ее разрешении.
1. Мегапиксели
Реклама пестрит: мегапиксели! Почему-то убеждая покупателя, что чем больше этих самых мегапикселей, тем лучше снимает камера.
Наверное, стоит пояснить, что такое пиксель. Пиксель – это элемент изображения, который состоит из 5ти частей, несущих информацию: яркость красного, яркость зеленого и яркость синих цветов, а также координаты по вертикали и горизонтали.
Эти данные позволяют процессору камеры правильно определять положение точек на матрице и их цвета. Все вместе пиксели образую кадр. В Мегапикселях (миллион пикселей) измеряют размер фотографии или отсканированного снимка.
2. Размер матрицы фотоаппарата
Однако матрица камеры, на которую записывается информация, имеет определенные размеры. За стандарт матрицы цифрового фотоаппарата принят размер пленочного кадра 24х35мм. В зависимости от типа камеры матрицы могут быть меньше или равны этому формату.
Ниже вы можете увидеть соотношение физических размеров матрицы некоторых моделей цифровых фотоаппаратов к стандартному размеру пленки в 35 мм. У компактов размер матрицы принято указывать в виде формулы 1/х ” (где «х» может быть целым или дробным числом, например 1/1,7, 1/2,5 и т. п.), а у зеркальных камер указываются физические размеры матрицы в мм (например, 22,2×14,8 мм или 24х36 мм).
Компактные камеры:
- Матрица размером 1 / 3.
 2″ – самые маленькие матрицы, соотношение сторон 4:3, физический размер 3.4 х 4.5 кв.мм;
2″ – самые маленькие матрицы, соотношение сторон 4:3, физический размер 3.4 х 4.5 кв.мм; - Матрица размером 1 / 2.7″ , соотношение сторон 4:3, физический размер 4.0 х 5.4 кв.мм;
Хорошие компактные камеры и псевдозеркалки
- Матрица размером 1 / 2,5″, соотношение сторон 4:3, то есть 4,3 х 5,8 кв.мм;
- Матрица размером 1 / 1,8″ , соотношение сторон 4:3, геометрический размер 5,3 х 7,2 кв.мм;
Дорогие компактные камеры и компактных камерах со сменной оптикой
- Матрица размером 2 / 3″ , соотношение сторон 4:3, физический размер 6,6 х 8,8 кв.мм ;
- Матрица размером 4 / 3″ , физический размер 18 х 13,5 кв.мм, соотношение сторон 4:3;
Бюджетные и полупрофессиональные зеркальные камеры
- DX, APS-C формат, соотношение сторон 3:2, размер около 24 х 18 кв.мм. Матрицы таких размеров соответствуют “полукадру” 35 мм кадра.
3. Как это все совмещается
Чем больше размер матрицы фотоаппарата, тем комфортнее чувствуют себя светочувствительные элементы – пиксели: расстояние между ними больше, перегреваются они меньше и, следовательно, лучше восприимчивость матрицы к свету.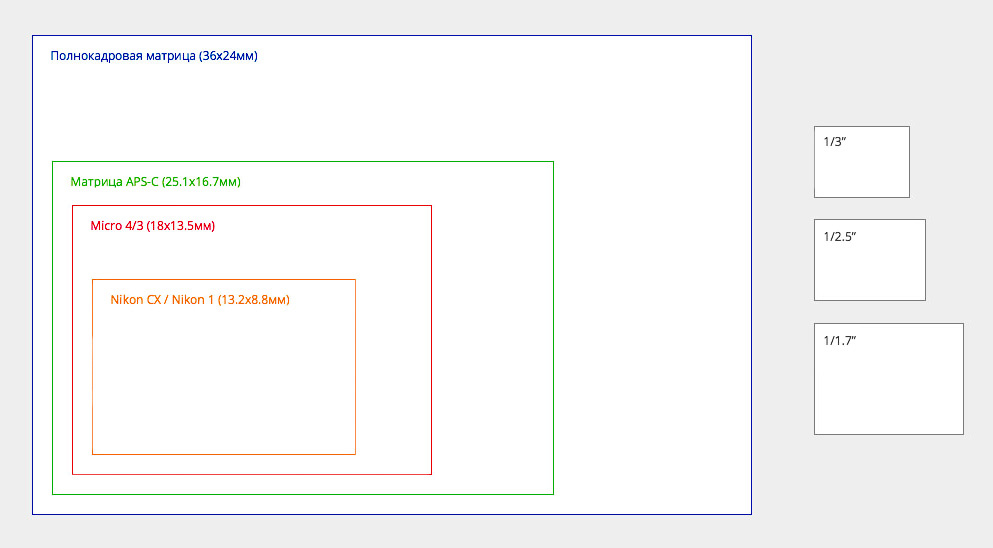 И тем качественнее получится снимок. Даже при одинаковом количестве пикселей качество фотографий с разных фотокамер может оказаться разным.
И тем качественнее получится снимок. Даже при одинаковом количестве пикселей качество фотографий с разных фотокамер может оказаться разным.
Что бы ни кричала реклама, число мегапикселей определяет лишь максимальный размер отпечатка, который можно получить с фотографии. И совсем уж мегапиксели не связаны с качеством изображения в отличие от размера матрицы цифровых фотоаппаратов. Ведь по факту даже разрешения 2 Мп достаточно, чтобы напечатать изображение хорошего качество размером 10*15. А 4Мп подойдут прекрасно для фотографии формата А4.
Поэтому гораздо более важно не количество пикселей, а их размер. Ведь если на маленькую матрицу запихнуть, скажем, 8Мп, то они будут очень маленькими. А чем меньше размер пикселя, тем выше уровень шума изображения. В компактных камерах и большинстве зеркалок нежелательные эффекты сглаживает встроенная программа шумоподавления, но эффект от нее — замыленность снимка.
Большое количество компактных любительских камер имеет разрешение матрицы фотоаппарата от 5 до 12 Мп, у зеркалки же этот диапазон составляет от 8 до 21 МП, при этом размер матрицы гораздо больше. В настройках камеры всегда можно выбрать разрешение снимка. Советую устанавливать этот параметр, ориентируясь на золотую середину, – такого разрешения вполне достаточно, чтобы получить четкую и красочную картинку.
В настройках камеры всегда можно выбрать разрешение снимка. Советую устанавливать этот параметр, ориентируясь на золотую середину, – такого разрешения вполне достаточно, чтобы получить четкую и красочную картинку.
Чтобы лучше объяснить соотношение количества пикселей и размера матрицы, приведу простой пример. Допустим, нужно посадить на грядке кусты клубники. Чем больше грядка, тем больше кустов можно посадить. Но если попытаться втиснуть на кусок земли 20 кв.м. 5 кустов, то в итоге вырастет сорняк.
Так и с пикселями: количество пикселей может быть одинаковым, но у «взрослой» камеры они будут на большей площади и смогут собрать больше света. А больше света — это, как правило, меньше шума и более широкий динамический диапазон.
Надеюсь, я все доступно объяснила. Удачи вам в выборе фотокамеры!
Ознакомьтесь с обзором матриц, формирующих фотоизображение. Часть 1
Владимир Нескоромный
Главный редактор сайта alphapro. sony.ru
sony.ru
В потребительской технике всегда торжествует компромисс, о котором мы совершенно не задумываемся. Например, наше представление о передаче трехмерного пространства на плоской, двумерной фотографии, как правило, сводится к фокусному расстоянию объектива. Широкоугольник охватывает много объектов, телеобъектив — мало, кроме того, он уменьшает эффект пространственной перспективы. Но как, к примеру? 16-мм объектив, являясь широкоугольным для полнокадровой зеркалки, превращается в телевик для компактной камеры?
В поисках нормального объектива
Следует понимать, что характеристики объектива определяются не только (и не столько) его фокусным расстоянием, сколько размером светочувствительного элемента. В зависимости от эпохи, аналоговой или цифровой, это — кадр пленки или матрицы. Именно отношение фокусного расстояния объектива к диагонали кадрового окна и служит мерой нормальности объектива для фотоаппарата, с которым он используется. Если этот показатель значительно меньше единицы, объектив является широкоугольным, если больше — длиннофокусным, близок к единице — нормальный. Напомним, что для кадра 24х36 мм с диагональю 43,3 мм нормальными являются объективы с фокусным расстоянием f=40-60 мм; для среднего формата 6-см пленки граница нормальности f=70 мм; для полукадра 18х24 мм — f=30 мм.
Если этот показатель значительно меньше единицы, объектив является широкоугольным, если больше — длиннофокусным, близок к единице — нормальный. Напомним, что для кадра 24х36 мм с диагональю 43,3 мм нормальными являются объективы с фокусным расстоянием f=40-60 мм; для среднего формата 6-см пленки граница нормальности f=70 мм; для полукадра 18х24 мм — f=30 мм.
Как формат определяет конечное качество изображения
Размер кадра пленки или матрицы определяет не только «перспективные» особенности получаемого изображения. В фотоиндустрии именно размер кадра, или формат, является компромиссным выбором, который необходим для выполнения различных требований.
Во-первых, размер кадра определяет габариты самой камеры — большая или компактная. Во-вторых, размер кадра важен для достижения необходимой светочувствительности и детализации изображения. В-третьих, он косвенно определяет возможность и степень управления глубиной резкости. Например, в художественной портретной фотографии мы обычно стремимся к уменьшению глубины резкости.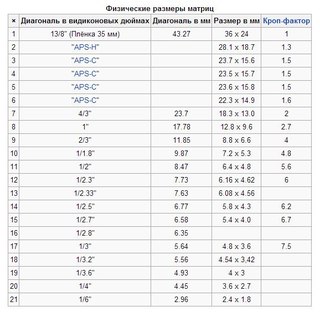 В пейзажной и технической, наоборот, к ее увеличению. В зависимости от того, какому требованию разработчики отдают предпочтение, реализуется то или иное решение.
В пейзажной и технической, наоборот, к ее увеличению. В зависимости от того, какому требованию разработчики отдают предпочтение, реализуется то или иное решение.
Фотограф может снимать на форматные пленки и сканирующие задники с размерами в десятки сантиметров, когда камера достигает метровых габаритов. А сотрудник спецслужбы — использовать для выполнения задания миниатюрную камеру-пуговицу в запонке. Но каждый их них получает необходимый результат и совершенно не переживает из-за своих габаритов фототехники.
Характеристики объектива определяются не только его фокусным расстоянием, сколько размером светочувствительного элемента. Именно отношение фокусного расстояния объектива к диагонали кадрового окна и служит мерой нормальности объектива для фотоаппарата, с которым он используется. Если этот показатель значительно меньше единицы, объектив является широкоугольным, если больше — длиннофокусным, близок к единице — нормальный.
О минусах миниатюризации
Удобство использования камеры определяется возможностью ее транспортирования и выполнения съемочных настроек с помощью кнопок, дисков, тачпэдов и сенсорного экрана. Аппарат с 10-сантиметровыми габаритами кажется наиболее эргономичным, и кадр форматом в несколько сантиметров как раз ему подходит. Но если понадобится сделать компактный телезум-объектив, чтобы носить камеру в кармане, то кадр придется уменьшить. Однако тут же возникает масса проблем. При значительном уменьшении размера кадра станет весьма затруднительно реализовать сложную механику управления, юстировку оптики, сохранить достаточную светочувствительность и разрешение. На практике с этим сталкиваются обладатели недорогих смартфонов. Стремление к миниатюризации приводит к повышенным шумам, завалам резкости и контраста по полю кадра из-за неточной юстировки оптики.
Аппарат с 10-сантиметровыми габаритами кажется наиболее эргономичным, и кадр форматом в несколько сантиметров как раз ему подходит. Но если понадобится сделать компактный телезум-объектив, чтобы носить камеру в кармане, то кадр придется уменьшить. Однако тут же возникает масса проблем. При значительном уменьшении размера кадра станет весьма затруднительно реализовать сложную механику управления, юстировку оптики, сохранить достаточную светочувствительность и разрешение. На практике с этим сталкиваются обладатели недорогих смартфонов. Стремление к миниатюризации приводит к повышенным шумам, завалам резкости и контраста по полю кадра из-за неточной юстировки оптики.
Эпоха полного кадра
Следующее требование — обеспечение требуемого разрешения и светочувствительности. Изображение элемента снимаемого объекта регистрируется ячейкой сенсора или светочувствительным кристаллом пленки. Чем они (ячейка и кристалл) больше, тем больше светового потока смогут захватить. Соответственно, вполне закономерное желание — использовать светочувствительные элементы покрупнее. Однако возникает другая задача — разрешение, количество пикселей или кристаллов.
Соответственно, вполне закономерное желание — использовать светочувствительные элементы покрупнее. Однако возникает другая задача — разрешение, количество пикселей или кристаллов.
Чтобы увеличить разрешение, нужно увеличить размеры матрицы или кадра пленки. С пленкой проще — просто перейти на больший формат, например, 6х9 см или 4х5 дюймов.
А вот увеличивать размеры матрицы слишком дорого. Только к настоящему времени доступная цельная матрица доросла до полного кадра 24х36 мм. А ведь в свое время компании-производители даже сращивали две недорогие маленькие матрицы в одну большую. Например, такое решение было реализовано в камере Minolta RD-3000, выпущенной в 1999 году. В ней две матрицы по 1,5 Мпикс. с помощью призмы формировали изображение с финальным разрешением 2,7 Мпикс.
Ограничения в гонке мегапикселей
Чтобы повысить разрешение, приходится уменьшать размер регистрирующего элемента сенсора при сохранении формата матрицы. К сожалению, и для пленки, и для матрицы существует физический предел уменьшения размера отдельного элемента. А значит, что и у разрешения тоже есть свой предел. Речь идет о дифракционном рассеянии света, обусловленное ограниченностью размера объектива. Оно накладывает ограничение на минимальный шаг между светочувствительными элементами матрицы.
А значит, что и у разрешения тоже есть свой предел. Речь идет о дифракционном рассеянии света, обусловленное ограниченностью размера объектива. Оно накладывает ограничение на минимальный шаг между светочувствительными элементами матрицы.
Например, чтобы раскрыть потенциал по разрешению объектива с диафрагмой f/2, достаточно использовать матрицу с минимальной дистанцией между светочувствительными элементами около одного микрона.
Использовать матрицу с шагом меньше 3 микрон с оптикой со светосилой f/5.6 не имеет смысла, поскольку пятно дифракционного рассеяния растет пропорционально диафрагменному числу.
В случае с пленочной фотографией ограничением на разрешение является структура фотоэмульсии. Хотя размер светочувствительного кристалла современных пленок и близок к одному микрону, но их распределение в слое эмульсии толщиной в несколько микрометров ограничивает разрешающую способность обычной фотопленки примерно 10 микронами (100 линий/мм).
Маленькие шаги на пути к гигантскому разрешению
А что происходит в цифровой фотографии, где матрица с шагом в один микрон уже стала реальностью? Попробуем оценить желаемую мегапиксельность полнокадровой матрицы 24х36 мм с шагом ячеек в один микрон применительно к объективу со светосилой f/2.
Тысяча элементов на миллиметр в пересчете на общее разрешение матрицы составят 24000х36000 или почти 900 Мпикс.! К сожалению, современная электроника не способна поддерживать такую матрицу, а именно, эффективно считывать и сохранять получаемый гигантский объем информации. Про массовый выпуск таких матриц мы даже не говорим.
В настоящее время в системных камерах Sony устанавливают полнокадровые матрицы с разрешением 42,4 Мпикс. и шагом 4,5 микрона (ILCE-7RM2). Имеет ли смысл дальнейшее повышение разрешения? С точки зрения потребителя, несомненно. Однако с инженерных позиций, при современном уровне развития технологий вряд ли будет оправданным стремление к повышению разрешения до дифракционного предела. Неидеальность оптики (аберрации и ошибки юстировки, фокусировки) устанавливает свои, более грубые, чем дифракционный предел, ограничения на увеличение разрешения.
В тоже время компания Sony наращивает линейку объективов серии G Master, которые способны поддерживать матрицы с разрешением в 100 Мпикс. Неужели нас ждет очередная сенсация?
Неужели нас ждет очередная сенсация?
Ну, а маленькие матрицы с шагом, близким к одному микрону, успешно используются в цифровых компактах и смартфонах.
Полнокадровая матрица в камере Sony A7R II. Разрешение 42,4 Мпикс.
О плюсах и минусах глубины резкости
Наконец, третья характеристика фотоизображения — глубина резкости. Для начала вспомним, что такое гиперфокальное расстояние. Мы видим резкими объекты не точно на дистанции наводки на резкость, а в некотором диапазоне около нее. И можно выбрать дистанцию наводки объектива так, что при установленной диафрагме все объекты от точки наводки на резкость и до бесконечности будут казаться резкими. Эта дистанция и есть гиперфокальное расстояние. Как правило, оно пропорционально квадрату фокусного расстояния и обратно пропорционально диафрагменному числу.
Если сравнивать результат, получаемый двумя камерами — с маленькой и большой матрицей, то окажется, что при равных условиях (угол охвата пространства и размер конечной картинки) гиперфокальное расстояние для камеры с меньшим фокусным расстоянием и небольшой матрицей будет меньше. Иными словами, при той же диафрагме на снимке компактной камеры зона резкости будет находиться ближе и будет шире, чем у камеры с большой матрицей. Это означает, что диафрагма f/2 компакта, на самом деле, вовсе не дает портретного эффекта с малой глубиной резкости, а работает как f/8-11 зеркалки или беззеркалки.
Иными словами, при той же диафрагме на снимке компактной камеры зона резкости будет находиться ближе и будет шире, чем у камеры с большой матрицей. Это означает, что диафрагма f/2 компакта, на самом деле, вовсе не дает портретного эффекта с малой глубиной резкости, а работает как f/8-11 зеркалки или беззеркалки.
Для портретов это, может быть, и не очень здорово, а для предметной и макросъемки, наоборот, просто замечательно. Ведь за увеличение глубины резкости не нужно платить диафрагмированием объектива, длинной выдержкой, повышением светочувствительности и, в конце концов, чистотой картинки (шумами) и резкостью.
Заключение
На фоторынке сейчас можно встретить самые различные предложения. Однако чтобы хорошо ориентироваться в них, следует знать основные параметры фототехники и понимать важность каждого их низ применительно к своим задачам. Собственно, мы их изучили. Теперь можно переходить к выбору конкретной камеры, и этой теме посвящен следующий материал.
Продолжение материала (часть 2) читать здесь.
типы, размер, разрешение, светочувствительность, чистка
Ни один фотоаппарат не может обойтись без матрицы. Современные модели оснащаются ей практически поголовно. Так произошло в момент, когда цифровые аналоги начали вытеснять устаревшие пленочные технологии. Матрица фотоаппарата является одним из основных компонентов, без которых невозможна эксплуатация всего прибора в целом, ведь его роль если и не является ключевой, то, по крайней мере, может считаться одной из ведущих. Именно матрица отвечает за качество будущего снимка, цветопередачу, четкость, полноту кадра. Как и другие важные элементы фототехники, матрица обладает рядом основных параметров, на которые обычно принято ориентироваться при выборе той или иной модели.
Типы матриц
Матрица цифрового фотоаппарата – это, в первую очередь, микросхема. Она преобразует световые лучи, которые, преломившись в системе линз и зеркал, попадают на нее. В результате такого преображения получается электрический сигнал, который выводится в цифровом виде, образуя снимок. За весь этот процесс отвечают специальные фотодатчики, расположенные на самой плате. Чем больше количество датчиков, чувствительных к свету, тем больше разрешение, и, как следствие, качество конечного снимка.
В результате такого преображения получается электрический сигнал, который выводится в цифровом виде, образуя снимок. За весь этот процесс отвечают специальные фотодатчики, расположенные на самой плате. Чем больше количество датчиков, чувствительных к свету, тем больше разрешение, и, как следствие, качество конечного снимка.
Встречаются матрицы следующих типов.
- ПЗС – тип матрицы фотоаппарата, который дословно расшифровывается как прибор зарядовой связи. В английском варианте – Charge-Coupled Device. Весьма известная аббревиатура, которая, впрочем, не так часто встречается в наши дни. Многие используют приборы, в основе которых лежат светодиоды, имеющие высокую светочувствительность, созданные на основе ПЗС системы, но, несмотря на широкую распространенность, данный вид микросхем все больше вытесняется более современным.
- КМОП-матрица. Формат матрицы, введенный в эксплуатацию в 2008 году. Впрочем, история создания данного формата уходит корнями в далекий 93-й, когда впервые была опробована технология APS.
 КМОП-матрица – это комплиментарный металл-оксид-полупроводник. Данная технология позволяет производить выборку отдельного пикселя почти так же, как и в стандартной системе памяти, к тому же, каждый пиксель оснащается дополнительным усилителем. Поскольку данная система является более современной, она зачастую оснащается автоматической подстройкой времени экспонирования каждого пикселя по отдельности. Данное улучшение позволяет получить полный кадр без потери боковых границ, а так же без потери верха и низа кадра. Полноразмерная матрица чаще всего бывает выполнена по технологии КМОП.
КМОП-матрица – это комплиментарный металл-оксид-полупроводник. Данная технология позволяет производить выборку отдельного пикселя почти так же, как и в стандартной системе памяти, к тому же, каждый пиксель оснащается дополнительным усилителем. Поскольку данная система является более современной, она зачастую оснащается автоматической подстройкой времени экспонирования каждого пикселя по отдельности. Данное улучшение позволяет получить полный кадр без потери боковых границ, а так же без потери верха и низа кадра. Полноразмерная матрица чаще всего бывает выполнена по технологии КМОП. - Существует еще один тип матрицы – Live-MOS-матрица. Ее выпустила фирма «Панасоник». Данная микросхема функционирует при помощи технологии, в основе которых лежит МОП. МОП-матрица позволяет делать качественные профессиональные снимки без высокого уровня шума, а также исключает перегрев.
Физический размер матрицы
Размер матрицы фотоаппарата – одна из ее важнейших характеристик. Как правило, его указывают в дюймах в виде дроби. Больший размер подразумевает меньшее количество шумов на конечном снимке. К тому же, чем больше физический размер, тем больше световых лучей способна зарегистрировать матрица. Объем и количество лучей напрямую влияют на качество передачи оттенков и полутонов.
Как правило, его указывают в дюймах в виде дроби. Больший размер подразумевает меньшее количество шумов на конечном снимке. К тому же, чем больше физический размер, тем больше световых лучей способна зарегистрировать матрица. Объем и количество лучей напрямую влияют на качество передачи оттенков и полутонов.
Кроп-фактор — это соотношение размеров кадра пленочного фотоаппарата 35 мм к размерам матрицы цифрового фотоаппарата. Все дело в том, что процесс создания цифровой матрицы довольно дорогостоящий, и поэтому производители постарались максимально сократить ее размер.
Если сравнить фото, сделанное с одним объективом на фотоаппарате с полнокадровой матрицей и фотоаппарате с «кропнутой» матрицей, то в первом случае угол охвата будет больше, и само изображение шире. Получается, что кропнутая матрица обрезает готовую картинку, отсюда и пошло такое название – кроп от англ. crop (резать).
Чаще всего кроп-фактор используют для замера наиболее точного расстояния фокуса у объектива, устанавливая его на различные приборы. Здесь вступает в игру такое понятие, как эквивалентное фокусное расстояние (ЭФР), которое вычисляется путем умножения фокусного расстояния (ФР) на кроп-фактор. Так, объектив с полнокадровой матрицей (кроп=1) и объективом с ФР 50 мм зафиксирует такое же по размерам изображение, как и кропнутая матрица 1,6 с объективом с ФР 30 мм. В этом случае можно сказать, что ЭФР у этих объективов одинаковое. Ниже приведена таблица, в которой можно провести сравнение, как меняется ЭФР в зависимости от кроп-фактора.
Здесь вступает в игру такое понятие, как эквивалентное фокусное расстояние (ЭФР), которое вычисляется путем умножения фокусного расстояния (ФР) на кроп-фактор. Так, объектив с полнокадровой матрицей (кроп=1) и объективом с ФР 50 мм зафиксирует такое же по размерам изображение, как и кропнутая матрица 1,6 с объективом с ФР 30 мм. В этом случае можно сказать, что ЭФР у этих объективов одинаковое. Ниже приведена таблица, в которой можно провести сравнение, как меняется ЭФР в зависимости от кроп-фактора.
Количество мегапикселей и разрешение матрицы
Матрица сама по себе является дискретной. Она состоит более чем из миллиона элементов, которые и преобразовывают световой поток, идущий от линз. В характеристике каждой модели фотоаппарата можно отыскать такой параметр матричной платы как количество светочувствительных элементов или разрешение матрицы, измеряемое в мегапикселях.
Один мегапиксель равен одному миллиону светочувствительных датчиков, улавливающих преломленные в линзах лучи.
Разумеется, чем этот параметр будет больше, тем лучший снимок получится сделать.
Правда, здесь есть и обратная зависимость. Если физический размер матрицы меньше, то и количество мегапикселей должно быть пропорционально меньше, в противном случае не удастся избежать эффекта дифракции: фотографии будут замыленными, без четкости.
Чем больше размер пикселя, тем больше он способен зафиксировать лучей, падающих на него. Размер пикселей напрямую связан с размерами матрицы, и влияет, в основном, на широту кадра. Чем больше количество мегапикселей с правильным соотношением размеров матрицы, тем больше лучей света смогу уловить датчики. Количество зафиксированных лучей напрямую влияет на исходные параметры преобразуемого материала: резкость, цветность, объем, контрастность, фокус.
Таким образом, разрешение фотокамеры влияет на качество снимка. Зависимость разрешения от объема использующихся пикселей очевидна. В объективе при помощи сложной расстановки оптических элементов формируется необходимый световой поток, который потом матрица поделит на пиксели. Оптические приборы тоже обладают собственным разрешением. Более того, если разрешение объектива достаточно мало, а передача двух светящихся точек, разделяемых одной темной, происходит как единого целого, то разрешение будет не столь отчетливо выделяться. Происходит это именно из-за прямой зависимости и привязки к числу мегапикселей.
Оптические приборы тоже обладают собственным разрешением. Более того, если разрешение объектива достаточно мало, а передача двух светящихся точек, разделяемых одной темной, происходит как единого целого, то разрешение будет не столь отчетливо выделяться. Происходит это именно из-за прямой зависимости и привязки к числу мегапикселей.
Важно: на качественный снимок влияет как параметр разрешения матрицы, так и разрешение оптики объектива. Измеряется оно количество линий на 1 мм. Своего максимального значения разрешение достигает, когда оба показателя — и матрица, и объектив — соответствуют друг другу.
Если говорить о разрешении современных цифровых микросхем, то оно складывается из размера пикселя (от 2 до 8 мкм). На сегодняшний день на рынке представлены модели с показателями до 30 мп.
Светочувствительность
В фотоаппаратах по отношению к матрице принято использовать термин эквивалентной чувствительности. Связано это с тем, что подлинную чувствительность можно измерять различными способами в зависимости от множества параметров матрицы. Зато, применив усиление сигнала и цифровую обработку, пользователь может обнаружить высокие пределы чувствительности.
Зато, применив усиление сигнала и цифровую обработку, пользователь может обнаружить высокие пределы чувствительности.
Параметры светочувствительности демонстрируют возможность исходного материала преобразовываться из электромагнитных воздействий потока света в электрический двоичный сигнал. Проще говоря, показывать, сколько требуется света для получения объективного уровня электрического импульса на выходе.
Параметр чувствительности (ISO) чаще всего используется фотографами для демонстрации возможности съемки в условиях плохого освещения. Увеличение чувствительности в параметрах прибора позволяет улучшить качество конечного снимка при необходимом значении диафрагмы и выдержки. ISO может достигать значения от нескольких десятков до тысяч и десятков тысяч единиц. Негативной стороной высоких значений светочувствительности является появление «шумов», которые проявляются в виде эффекта зернистости кадра.
Как проводить чистку матрицы в домашних условиях
Битые пиксели не всегда могут быть таковыми на самом деле.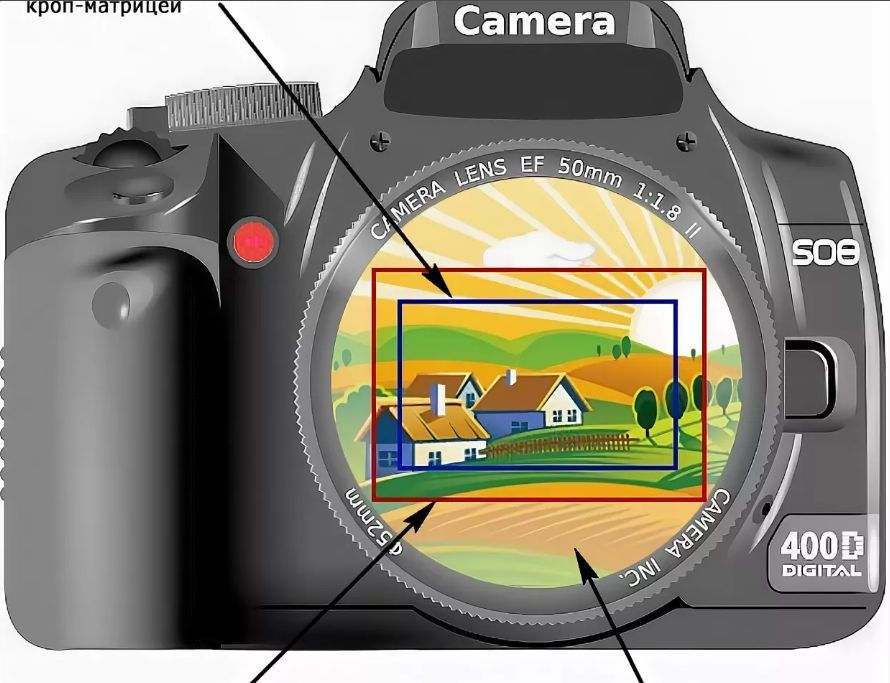 В действительности, когда происходит смена объектива, на матрицу могут попасть частицы мусора, вызывающие эффект «битого пикселя». Чистка матрицы фотоаппарата нужна для профилактики этого эффекта, а также для более комфортной работы с прибором.
В действительности, когда происходит смена объектива, на матрицу могут попасть частицы мусора, вызывающие эффект «битого пикселя». Чистка матрицы фотоаппарата нужна для профилактики этого эффекта, а также для более комфортной работы с прибором.
Со временем, в особенности, если устройство эксплуатируется подолгу в различных погодных условиях, матрица может покрыться слоем пыли. При нарушении герметичности в области крепления объектива на поверхность может попасть небольшое количество влаги, что тоже может негативно сказаться на качестве кадра. Чистку можно доверить профессионалам из сервисного центра, а можно провести и самостоятельно, в домашних условиях.
Важно не забывать, что помещение, в котором будет происходить процедура, должно быть как можно менее пыльным, без сильных сквозняков. Прежде чем приступать к самой процедуре, необходимо убедиться, что аккумуляторная батарея заряжена.
Первый и самый простой способ очистки стеклянной поверхности кремниевой пластины микросхемы – сдувание пыли. Для этого следует использовать самую обычную грушу для чистки объективов, она продается в любом крупном магазине бытовой техники. К сожалению, использование груши помогает только при снятии легкого налета небольших песчинок пыли. Для более крупных частиц, которые могли прилипнуть к поверхности, может потребоваться что-то более основательное.
Для этого следует использовать самую обычную грушу для чистки объективов, она продается в любом крупном магазине бытовой техники. К сожалению, использование груши помогает только при снятии легкого налета небольших песчинок пыли. Для более крупных частиц, которые могли прилипнуть к поверхности, может потребоваться что-то более основательное.
Если груша не помогла справиться с пятнами на матрице, можно попробовать использовать специальный набор для очистки стеклянной поверхности. Стоит он несколько дороже, но эффективность очистки значительно выше.
- Первый пункт в очистке – использование специального пылесоса. Его сборка не занимает много времени и детально описана в инструкции к набору. На конце устройства находится мягкий наконечник, так что повреждение прибора во время работы исключено. Лучше всего будет прочистить при помощи пылесоса не только стеклянную поверхность, но и все скрытые полости, доступные для чистки.
- После уборки при помощи пылесоса можно начинать влажную уборку.
 Она осуществляется при помощи специальных щеточек, одна из которых влажная, другая сухая. Этот вид уборки нужен для пылинок, которые, будучи мокрыми, попали на поверхность стекла, и, высохнув, прикрепились к нему, создав эффект «битого пикселя». Влажная щетка пропитана специальным раствором, который эффективно удаляет засохшие песчинки и пылинки, не оставляя пятен и разводов. Необходимо проводить по стеклу плавными аккуратными движениями, лишь слегка нажимая на саму щетку. Оставшаяся влага довольно быстро испарится сама. Даже если после влажной уборки на стекле остается пара капель, то они прекрасно удаляются сухой щеточкой (кисточкой).
Она осуществляется при помощи специальных щеточек, одна из которых влажная, другая сухая. Этот вид уборки нужен для пылинок, которые, будучи мокрыми, попали на поверхность стекла, и, высохнув, прикрепились к нему, создав эффект «битого пикселя». Влажная щетка пропитана специальным раствором, который эффективно удаляет засохшие песчинки и пылинки, не оставляя пятен и разводов. Необходимо проводить по стеклу плавными аккуратными движениями, лишь слегка нажимая на саму щетку. Оставшаяся влага довольно быстро испарится сама. Даже если после влажной уборки на стекле остается пара капель, то они прекрасно удаляются сухой щеточкой (кисточкой). - Третий этап – финальный, проводим сухой щеточкой по матрице и убеждаемся, что она чистая.
После очистки можно попробовать сделать тестовый снимок, чтобы убедиться, что процедура прошла успешно. Для этого необходимо закрыть диафрагму до максимального значения и сделать снимок чистого белого листа, приведя объектив в состояние полной расфокусировки. Затем сравнить качество снимков до и после.
Затем сравнить качество снимков до и после.
Почистить матрицу зеркального фотоаппарата довольно просто, для этого не требуется каких-то глубоких знаний или большого опыта, достаточно желания, немного терпения и знания базовых принципов очистки высокоточной оптической техники.
Заключение
Матрица фотоаппарата является важнейшей деталью любой современной зеркалки. Без нее невозможно сделать снимок, а от ее параметров зависит дальнейшее использование устройства. Если параметры матрицы выбраны неправильно, фотоаппарат не будет оптимально справляться со своими задачами. Матрица не требует какого-то дополнительного ухода, кроме периодической чистки стеклянной поверхности.
Следует отметить, что светочувствительные датчики очень хрупкие и плохо переживают падение прибора даже с небольшой высоты, поэтому эксплуатировать фотоаппарат рекомендуется с максимальной осторожностью и аккуратностью.
Matrix Market: форматы файлов
Matrix Market: форматы файловКратко опишем форматы файлов ASCII для матриц, распространяемых Матричный рынок:
Обратите внимание, что большинство файлов данных, которые мы распространяем, сжаты с использованием gzip , а некоторые представляют собой многофайловые архивы на основе Unix tar . Обратитесь к нашему документу о сжатии, если вам нужно помогите в расшифровке этих файлов.
Форматы обмена Matrix Market
Это собственный формат обмена для Matrix Market. Мы предоставляем только краткий обзор этого формата на этой странице; полный описание приведено в статье Форматы матричного рынка: первоначальный дизайн [Gziped PostScript, 51 Кбайт] [PostScript, 189 Кбайт].
Форматы обмена Matrix Market (MM) предоставляют простой механизм для
облегчить обмен матричными данными. В частности, цель была
для определения минимального базового формата файла ASCII, который можно очень легко объяснить
и разбирается, но может легко адаптироваться к приложениям с более жесткой структурой,
или расширен на связанные объекты данных. Формат обмена MM для матриц:
действительно набор дочерних форматов, которые разделяют элементы дизайна. В нашем
В исходной спецификации определены два формата матриц.
В частности, цель была
для определения минимального базового формата файла ASCII, который можно очень легко объяснить
и разбирается, но может легко адаптироваться к приложениям с более жесткой структурой,
или расширен на связанные объекты данных. Формат обмена MM для матриц:
действительно набор дочерних форматов, которые разделяют элементы дизайна. В нашем
В исходной спецификации определены два формата матриц.
- Формат координат
Формат файла, подходящий для представления общих разреженных матриц.Предусмотрены только ненулевые записи, и координаты каждого ненулевая запись указывается явно. Это показано в приведенном ниже примере. - Формат массива
Формат файла, подходящий для представления общих плотных матриц. Все записи представлены в заранее определенном (ориентированном на столбцы) порядке.
 (я.е., действительный, комплексный, целочисленный, шаблон) и структура симметрии, которая может
уменьшить размер файла данных (т.е. общий, симметричный, кососимметричный,
Эрмитова), сохраняя ненулевые элементы только на главной диагонали или ниже.
(я.е., действительный, комплексный, целочисленный, шаблон) и структура симметрии, которая может
уменьшить размер файла данных (т.е. общий, симметричный, кососимметричный,
Эрмитова), сохраняя ненулевые элементы только на главной диагонали или ниже.Формат координат MM подходит для представления разреженных матриц. Необходимо кодировать только ненулевые записи, и координаты каждой дано явно. Это проиллюстрировано на следующем примере реального Общая разреженная матрица 5×5.
1 0 0 6 0
0 10,5 0 0 0
0 0 .015 0 0
0 250,5 0 -280 33,32
0 0 0 0 12
В формате координат MM это можно представить следующим образом.%% MatrixMarket Координата матрицы вещественная общая % ================================================= ================================ % % Этот файл ASCII представляет собой разреженную матрицу MxN с L % ненулевые в следующем формате Matrix Market: % % + ---------------------------------------------- + % | %% MatrixMarket матричная координата вещественная общая |
Первая строка содержит код типа. В этом примере это означает, что
представляемый объект представляет собой матрицу в формате координат, и что числовой
следующие данные являются действительными и представлены в общем виде. (Под общими мы подразумеваем
что формат матрицы не использует никаких свойств симметрии.)
В этом примере это означает, что
представляемый объект представляет собой матрицу в формате координат, и что числовой
следующие данные являются действительными и представлены в общем виде. (Под общими мы подразумеваем
что формат матрицы не использует никаких свойств симметрии.)
Варианты формата координат определены для матриц со сложными и
целочисленные записи, а также те, в которых только позиция ненулевого
записей (шаблонных матриц).(Это будет обозначено
изменение вещественного числа на комплексное, целое или
узор соответственно в строке заголовка). Дополнительные варианты
определен для случаев, когда симметрия может быть использована для значительного уменьшения
размер данных: симметричный, кососимметричный и эрмитовый . В этих случаях только входы в нижнюю треугольную часть необходимо поставить . В кососимметричном
В этом случае диагональные элементы равны нулю, поэтому они также опускаются.(Эти
будет обозначено изменением общего на симметричный,
кососимметричный или эрмитовый соответственно по заголовку
линия).
Следующие пакеты программного обеспечения доступны для помощи в чтении и записи. матрицы в формате Matrix Market.
Harwell-Boeing Exchange Format
Формат Harwell-Boeing — самый популярный механизм для текстовых файлов. обмен разреженными матричными данными. Следующая информация, взято из Руководство пользователя коллекции разреженных матриц Harwell-Boeing предоставляет спецификацию для этого формата.Данные матрицы хранятся в 80 столбцах фиксированной длины. формат для переносимости. Каждая матрица начинается с кратного блок заголовка строки, за которым следуют два, три или четыре данных блоки. Блок заголовка содержит сводку информация о форматах хранения и требованиях к пространству. Из только блок заголовка, пользователь может определить, сколько пространство потребуется для хранения матрицы. Информация о размер изображения в строках приведен для удобства в пропуск ненужных данных.
Если нет правых векторов, матрица имеет
блок заголовка из четырех строк, за которым следуют два или три блока данных
содержащий, по порядку, начало столбца (или элемента)
указатели, индексы строк (или переменных) и числовые
значения. Если правые части присутствуют, есть пятая
строка в блоке заголовка и четвертый блок данных
содержащую правую часть (и). Блоки, содержащие
числовые значения и правая часть (и) необязательны.Правая часть (и) может присутствовать только тогда, когда
числовые значения присутствуют.
Если правые части присутствуют, то векторы для начальных догадок
и раствор также может присутствовать; если так, они отображаются как отдельные
полные массивы в правом блоке после правого
боковой вектор (ы).
Если правые части присутствуют, есть пятая
строка в блоке заголовка и четвертый блок данных
содержащую правую часть (и). Блоки, содержащие
числовые значения и правая часть (и) необязательны.Правая часть (и) может присутствовать только тогда, когда
числовые значения присутствуют.
Если правые части присутствуют, то векторы для начальных догадок
и раствор также может присутствовать; если так, они отображаются как отдельные
полные массивы в правом блоке после правого
боковой вектор (ы).
Первая строка содержит 72-символьный заголовок и
8-значный идентификатор, по которому ссылается матрица
в нашей документации.
Вторая строка содержит количество строк для каждого из
следующие блоки данных, а также общее количество строк,
за исключением блока заголовка.Третья линия
содержит трехсимвольную строку, обозначающую тип матрицы
а также количество строк, столбцов (или элементов),
элементов, а в случае несобранных матриц — всего
количество записей в элементарных матрицах. В
четвертая строка содержит переменные форматы Fortran для
следующие блоки данных. Пятая строка
присутствует, только если есть правые части. Он содержит один
символьная строка, обозначающая формат хранения для
правые части, а также количество правых частей,
и количество записей индекса строки (для собранного корпуса).Точный формат дается следующим, где имена
Переменные Fortran в последующих программах указаны в скобках:
Пятая строка
присутствует, только если есть правые части. Он содержит один
символьная строка, обозначающая формат хранения для
правые части, а также количество правых частей,
и количество записей индекса строки (для собранного корпуса).Точный формат дается следующим, где имена
Переменные Fortran в последующих программах указаны в скобках:
Линия 1 (A72, A8)
| Колонка 1 — 72 | Титул ( TITLE ) |
| Кол.73 — 80 | Ключ ( КЛЮЧ ) |
Строка 2 (5I14)
| Полковник1–14 | Общее количество строк без заголовка ( TOTCRD ) |
| Кол. 15 — 28 | Количество строк для указателей ( PTRCRD ) |
Кол. 29 — 42 29 — 42 | Количество строк для строковых (или переменных) индексов ( INDCRD ) |
| Кол.43 — 56 | Количество строк для числовых значений ( VALCRD ) |
| Полковник57 — 70 | Кол-во строк для правой стороны ( RHSCRD ) |
| (включая исходные предположения и векторы решений, если они есть) | |
| (ноль означает отсутствие данных с правой стороны) |
Строка 3 (A3, 11X, 4I14)
| Кол. 1 — 3 | Тип матрицы (см. Ниже) ( MXTYPE ) |
| Полковник15 — 28 | Количество строк (или переменных) ( NROW ) |
Кол. 29 — 42 29 — 42 | Количество столбцов (или элементов) ( NCOL ) |
| Кол.43 — 56 | Количество индексов строк (или переменных) ( NNZERO ) |
| (равно количеству записей для собранных матриц) | |
| Полковник57 — 70 | Количество элементов элементной матрицы ( NELTVL ) |
| (ноль в случае собранных матриц) |
Строка 4 (2A16, 2A20)
| Столбец 1 — 16 | Формат для указателей ( PTRFMT ) |
| Кол. 17 — 32 | Формат для индексов строк (или переменных) ( INDFMT ) |
| Полковник33–52 | Формат числовых значений матрицы коэффициентов ( VALFMT ) |
Кол.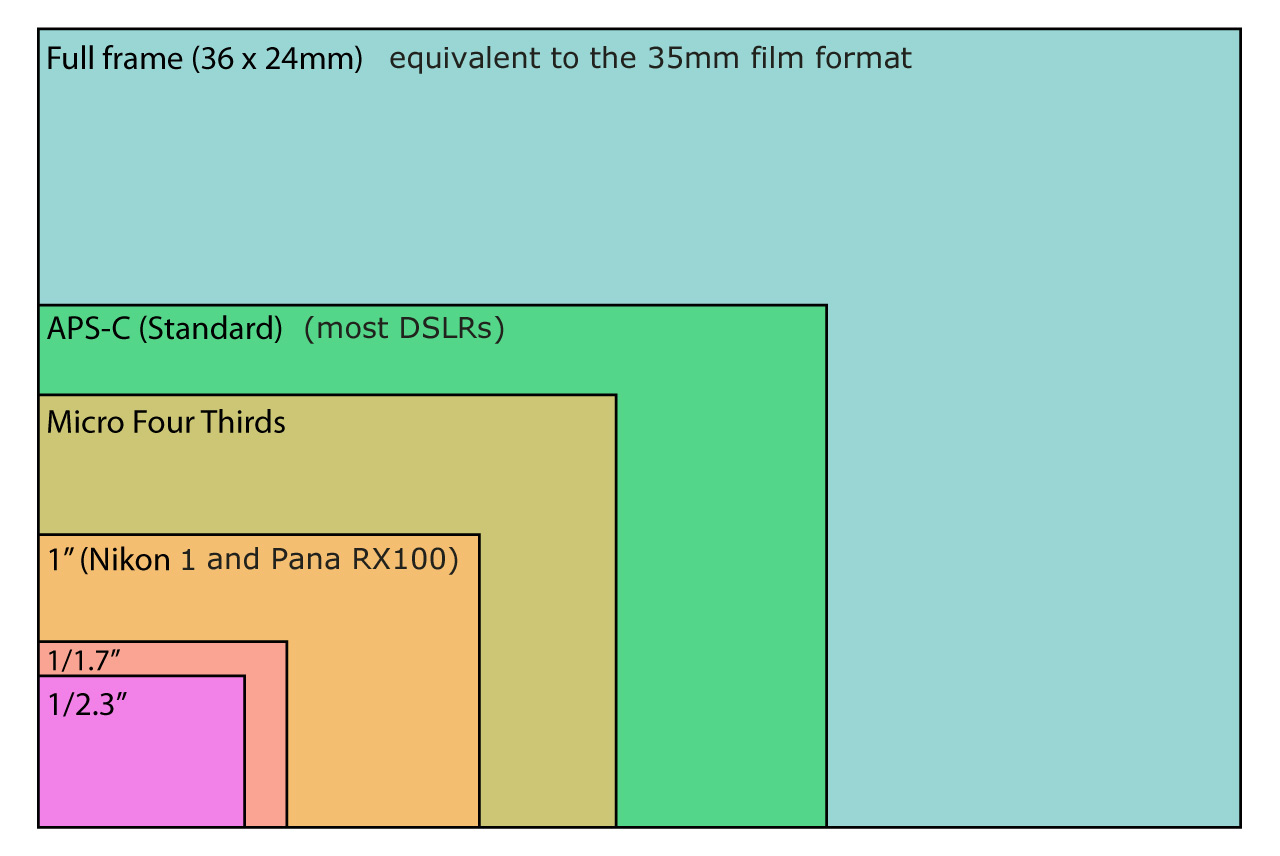 53 — 72 53 — 72 | Формат числовых значений правых частей ( RHSFMT ) |
Строка 5 (A3, 11X, 2I14) Присутствует только при наличии правых сторон
| Кол. 1 | Тип правой стороны: |
| F для полного хранения или | |
| M для того же формата, что и матрица | |
| Полковник2 | G , если задан начальный вектор (предположения). ( RHSTYP ) |
| Кол. 3 | X , если предоставлен точный вектор (ы) решения. |
| Кол. 15 — 28 | Количество правых сторон ( NRHS ) |
Кол. 29 — 42 29 — 42 | Количество индексов строк ( NRHSIX ) |
| (игнорируется в случае несобранных матриц) |
Примечание: Для матриц в элементарной форме два ведущих размера в в заголовке указано количество переменных в конечном элементе приложение и количество элементов.Обычно не все переменные в приложении появляются в линейной алгебре подзадача; следовательно, представленная матрица может быть более низкого порядка, чем первый параметр, описываемый как «количество переменных ( NROW ) «. Переменные конечных элементов пронумерованы от 1 до . NROW , г. , но только подмножество переменных, которые фактически появляются в списке переменные для элементов определяют строки и столбцы матрица.Фактический порядок квадратной матрицы не может быть определен пока не будут прочитаны все индексы.
Поле трехсимвольного типа в строке 3 описывает тип матрицы. В следующей таблице перечислены допустимые значения для каждого из трех
символы. В качестве примера поля типа RSA означает, что
матрица реальная, симметричная, собранная.
В следующей таблице перечислены допустимые значения для каждого из трех
символы. В качестве примера поля типа RSA означает, что
матрица реальная, симметричная, собранная.
Первый символ:
| R Реальная матрица |
| C Комплексная матрица |
| P Только шаблон (числовые значения не предоставляются) |
Второй символ:
| S Симметричный |
| U Несимметричный |
| H Эрмитский |
| Z Наклон симметричный |
| R прямоугольный |
Третий символ:
| A Собранный |
| E Элементные матрицы (в разобранном виде) |
Пример кода Fortran для чтения файлов Harwell-Boeing
Чтобы формализовать логическую блочную структуру данных, мы включены два образца кода FORTRAN для чтения матрица в формате набора тестов разреженных матриц. Оба кода
Предположим, что данные поступают от блока ввода LUNIT.
Нет и полного кода. Настоящий код должен содержать ошибку
проверка того, что целевые массивы, в которые
данные читаются достаточно большие. Дизайн позволяет
массивы для чтения отдельной подпрограммой, которая может избежать
использование возможно неэффективных неявных DO-циклов.
Оба кода
Предположим, что данные поступают от блока ввода LUNIT.
Нет и полного кода. Настоящий код должен содержать ошибку
проверка того, что целевые массивы, в которые
данные читаются достаточно большие. Дизайн позволяет
массивы для чтения отдельной подпрограммой, которая может избежать
использование возможно неэффективных неявных DO-циклов.Код выше описывает структуру данных. В интерпретация массивов индексов строк (или переменных) потребует знания матрицы и правой части типы, как читается в этом коде.
Процедуры Matlab для чтения / записи файлов Harwell-Boeing
Разработчики коллекции матриц NEP предоставили m-файл Matlab для написать разреженную матрицу Matlab в формате Harwell-Boeing. Также доступна версия для сложных матриц.
Группа тестирования и оптимизации Беркли (BeBOP) разработала библиотека и отдельная утилита для конвертации между Harwell-Boeing, Matrix Market, и форматы разреженных матриц MATLAB.
Текстовый файл с координатами
Примечание: Этот формат постепенно сокращается.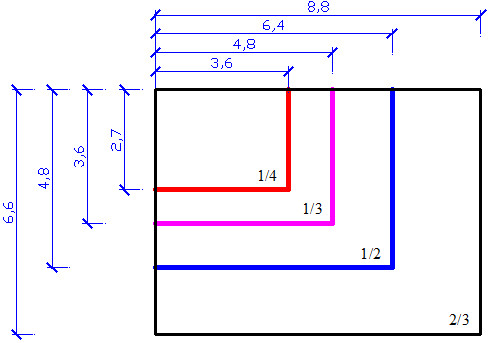
Текстовый формат координат обеспечивает простой и переносимый способ обмена разреженные матрицы. Любой язык или компьютерная система, которая понимает текст ASCII. можно прочитать этот формат файла с помощью простого цикла чтения. Это делает эти данные доступны не только пользователям в сообществе Fortran, но и разработчикам с использованием сред C, C ++, Pascal или Basic.
В формате текстового файла координат в первой строке перечислено три целых числа: число строк m , столбцов n и ненулевых nz в матрице. В затем перечисляются ненулевые матричные элементы, по одному в строке, путем указания индекса строки i , индекс столбца j и значение a (i, j) в указанном порядке. Например,
м м нз
i1 j1 val1
i2 j2 val2
i3 j3 val3
.. .
. . .
. . .
inz jnz valnz
Пробелы не имеют значения (т.е. фиксированный столбец не используется). Ненулевой
значения могут быть в виде с фиксированной или с плавающей запятой, для любого
точность (хотя Fortran и C обычно разбирают менее 20 значащих цифр). Например, допустимы следующие значения: 3, 3.141,
+ 3.1415626536E000, 3.1e0.
Например, допустимы следующие значения: 3, 3.141,
+ 3.1415626536E000, 3.1e0.
Эксперименты показывают, что эти файлы координат примерно на 30% больше, чем соответствующие файлы Harwell-Boeing.Версии, сжатые с помощью Unix compress или gzip обычно демонстрирует аналогичные соотношения.
Чтобы представить только структурную информацию разреженной матрицы, один ноль может быть помещенным в значение позиции, например
M N nz
i1 j1 0
i2 j2 0
i3 j3 0
. . .
. . .
. . .
inz jnz 0
Хотя доступны более эффективные схемы, это позволяет той же процедуре
читать оба типа файлов.Добавление одного байта к каждой строке
файл обычно не имеет большого значения. Обратите внимание, что нет никакого подразумеваемого порядка для элементов матрицы. Это позволяет
написать простые процедуры печати, которые пересекают разреженную матрицу в любом
естественный порядок, заданный конкретной схемой хранения.
Также обратите внимание, что аннотации не используются для хранения матриц со специальными структура. (Это упрощает процедуру синтаксического анализа.) Симметричные матрицы могут быть представлены только их верхней или нижней треугольной частью, но файл формат показывает только это — программа чтения видит только треугольник матрица. (Приложение отвечает за переосмысление этого.)
Доступна функция MATLAB (M-файл), которая считывает матрицу в координатах формат текстового файла и создает разреженную матрицу.
Матричный рынок — это услуга Отделение математических и вычислительных наук / Лаборатория информационных технологий / Национальный институт стандартов и технологий
[ Дома ] [ Поиск ] [Обзор] [ Ресурсы ]
Последнее изменение на этой странице: 14 августа 2013 .[
[email protected] ].Матричные форматы и ввод / вывод — документация Clustergrammer 1.1.0
Clustergrammer принимает в качестве входных данных:
Матричный файл, разделенный табуляцией, может принимать несколько форматов, показанных ниже, которые могут включать категории строк / столбцов и названия / названия категорий. Во всех случаях имена строк и столбцов должны быть уникальными (если имена входных данных не уникальны, к именам будут добавлены уникальные целые числа). Пользователям предлагается упорядочить свою матрицу с точками данных в виде столбцов и измерений в виде строк, что позволяет пользователям использовать преимущества интерактивного уменьшения размерности Clustergrammer.
Во всех случаях имена строк и столбцов должны быть уникальными (если имена входных данных не уникальны, к именам будут добавлены уникальные целые числа). Пользователям предлагается упорядочить свою матрицу с точками данных в виде столбцов и измерений в виде строк, что позволяет пользователям использовать преимущества интерактивного уменьшения размерности Clustergrammer.
Внешняя библиотека Clustergrammer-JS может визуализировать матрицы размером от ~ 500000 до ~ 1000000 ячеек, а также оптимизирована для визуализации матриц с большим количеством строк, чем столбцов — это было сделано для размещения наборов данных с большим количеством измерений (строк) и небольшим количеством измерения (столбцы), которые распространены в биологии. Однако для кластеризации очень больших матриц с помощью библиотеки Clustergrammer-PY может потребоваться много времени.
Простой формат матрицы
Самый простой формат файла с разделителями табуляцией показан здесь:
Col-A Col-B Col-C Ряд-A 0.0 -0,1 1,0 Ряд-B 3,0 0,0 8,0 Ряд-C 0,2 0,1 2,5
Первая строка содержит имена столбцов и начинается с пустой табуляции. Все остальные строки начинаются с имени строки, за которым следуют данные строки. Заголовки строк и столбцов можно добавить, добавив к имени каждой строки или столбца префикс «Заголовок:» (не показано в этом примере). См. Example_tsv.txt для примера этого формата матрицы.
Формат матрицы простых категорий
Категории строк и столбцов можно включить двумя способами.Первый формат простой категории показан ниже:
Матрица с категориями строк и столбцов в «простом» формате.
Этот формат простой категории позволяет пользователям кодировать категории столбцов как дополнительные строки под метками столбцов и категории строк как дополнительные столбцы рядом с метками строк. На приведенном выше снимке экрана электронной таблицы Excel показана категория с одной строкой, добавляемая в качестве дополнительного столбца строк (например, Тип: Интересно, ), и категория с одним столбцом, добавляемая в качестве дополнительной строки строк (например, Тип: Интересно, ). грамм.
грамм. Пол: мужской ). Таким же образом можно добавить до 15 категорий. Заголовки для названий строк или столбцов или категорий могут быть добавлены путем добавления к каждой строке префикса 'Title:' (обратите внимание на пробел после двоеточия). Например, заголовок имен столбцов — Строка ячеек , а заголовок категорий строк — Пол . См. Rc_two_cats.txt для примера этого формата матрицы. Заголовки, если они заданы, будут отображаться в виде меток над именами строк / столбцов или рядом с категориями строк / столбцов.
Формат матрицы категорий кортежей
Имена и категории строк / столбцов также могут быть закодированы как кортежи Python, как показано ниже:
('Cell Line: A549', 'Gender: Male') ('Cell Line: h2299', 'Gender: Female') ('Cell Line: H661', 'Gender: Female')
('Ген: EGFR', 'Тип: Интересный') -3,234 5,03 0,001
('Ген: TP53', 'Тип: не интересно') 8,3 4,098 -12,2
('Ген: IRAK', 'Тип: не интересно') 7,23 3,01 0,88
С форматом категорий кортежей легче работать в Python, и он может быть импортирован / экспортирован в Pandas DataFrames и как файлы, разделенные табуляцией. Обратите внимание, что заголовки были добавлены к именам и категориям строк / столбцов, как описано выше. См. Tuple_cats.txt для примера этого формата матрицы.
Обратите внимание, что заголовки были добавлены к именам и категориям строк / столбцов, как описано выше. См. Tuple_cats.txt для примера этого формата матрицы.
Типы категорий: строка и значение
Категории строк и столбцов могут быть типа: строка или значение . Если категории указаны в виде строк (например, содержат буквы), тогда категории будут отображаться с использованием цветов. Если категории относятся к типу значения (например, все категории содержат только числа), тогда категории значений будут отображаться с использованием цвета и непрозрачности (серый для положительного и оранжевый для отрицательного).
Value Категории на основе могут быть полезны для добавления данных в вашу визуализацию (например, значения дозировки лекарства), которые вы хотели бы сравнить с другими вашими измерениями, но это не должно влиять на вашу кластеризацию. И значение, и , и строка. Категории также можно использовать для изменения порядка в матрице, дважды щелкнув их метки (см.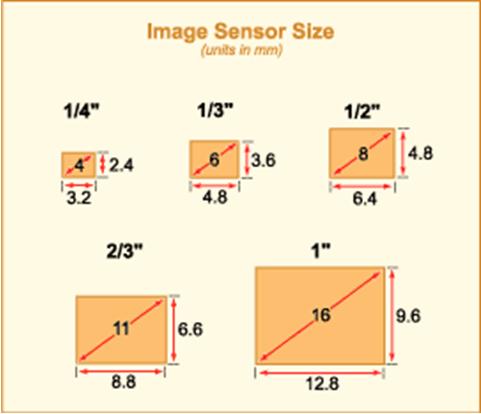 «Интерактивные категории»).
«Интерактивные категории»).
Примеры файлов матрицы
Несколько примеров файлов матриц, разделенных табуляцией, можно найти в примерах файлов матриц.
Матричный ввод / вывод в Clustergrammer.py
Clustergrammer-PY может загружать матрицу непосредственно из файла или из Pandas DataFrame, а также экспортировать в файл или Pandas DataFrame (для получения дополнительной информации см. Clustergrammer-PY API):
# инициализировать сетевой объект
из сети импорта clustergrammer
net = Сеть ()
# загрузить матрицу из файла или DataFrame
##################################
# загрузить данные из файла
net.load_file ('your_matrix.txt')
# загружаем данные из DataFrame, df
сеть.load_df (df)
# экспортная матрица
###############
# записываем матрицу в файл, разделенный табуляцией
net.write_matrix_to_tsv (имя файла)
# экспортировать данные в Pandas DataFrame
df_export = net.export_df ()
матриц и массивов — MATLAB & Simulink
MATLAB — это сокращение от «матричная лаборатория». В то время как другие языки программирования в основном работают с числами по одному, MATLAB® разработан для работы в основном с целыми матрицами и массивами.
В то время как другие языки программирования в основном работают с числами по одному, MATLAB® разработан для работы в основном с целыми матрицами и массивами.
Все переменные MATLAB — это многомерные массивы , независимо от типа данных.Матрица представляет собой двумерный массив, часто используемый в линейной алгебре.
Создание массива
Чтобы создать массив из четырех элементов в одной строке, разделите элементы запятой (, ) или пробелом.
Этот тип массива представляет собой вектор-строку .
Чтобы создать матрицу, состоящую из нескольких строк, разделите строки точкой с запятой.
a = [1 2 3; 4 5 6; 7 8 10]
a = 3 × 3
1 2 3
4 5 6
7 8 10
Другой способ создать матрицу — использовать функцию, например, единиц , нулей или рандом .Например, создайте вектор-столбец из нулей размером 5 на 1.
Операции с матрицами и массивами
MATLAB позволяет обрабатывать все значения в матрице с помощью одного арифметического оператора или функции.
ANS = 3 × 3
11 12 13
14 15 16
17 18 20
ANS = 3 × 3
0,8415 0,9093 0,1411
-0,7568 -0,9589 -0,2794
0,6570 0,9894 -0,5440
Чтобы транспонировать матрицу, используйте одинарную кавычку ( '):
ans = 3 × 3
1 4 7
2 5 8
3 6 10
Вы можете выполнить стандартное матричное умножение, которое вычисляет внутренние произведения между строками и столбцами, используя оператор * .Например, подтвердите, что матрица, умноженная на обратную, возвращает единичную матрицу:
p = 3 × 3
1,0000 0 0
0,0000 1,0000 0
0,0000 -0,0000 1,0000
Обратите внимание, что p не является матрицей целых значений. MATLAB хранит числа как значения с плавающей запятой, а арифметические операции чувствительны к небольшим различиям между фактическим значением и его представлением с плавающей запятой. Вы можете отобразить больше десятичных цифр с помощью команды format :
p = 3 × 3 1.000000000000000 0 0 0,000000000000002 1,00000000000000000 0 0.000000000000002 -0.000000000000004 1.000000000000000
Сбросьте отображение на более короткий формат, используя формат
влияет только на отображение чисел, а не на то, как MATLAB вычисляет или сохраняет их.
Чтобы выполнить поэлементное умножение, а не матричное умножение, используйте оператор . * :
p = 3 × 3
1 4 9
16 25 36
49 64 100
Каждый матричный оператор умножения, деления и мощности имеет соответствующий оператор массива, который работает поэлементно.Например, возвести каждый элемент из a в третью степень:
ans = 3 × 3
1 8 27
64 125 216
343 512 1000
Конкатенация
Конкатенация — это процесс объединения массивов в более крупные. Фактически, вы создали свой первый массив, объединив его отдельные элементы. Пара квадратных скобок [] — это оператор конкатенации.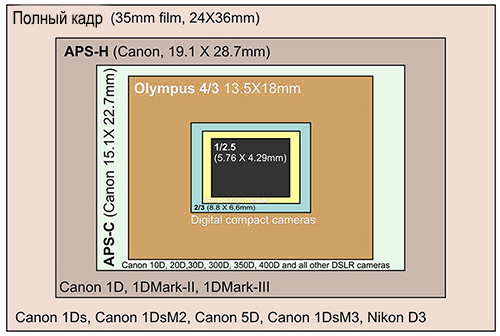
A = 3 × 6
1 2 3 1 2 3
4 5 6 4 5 6
7 8 10 7 8 10
Объединение массивов рядом друг с другом с использованием запятых называется объединением по горизонтали .Каждый массив должен иметь одинаковое количество строк. Точно так же, когда массивы имеют одинаковое количество столбцов, вы можете объединить по вертикали и , используя точки с запятой.
A = 6 × 3
1 2 3
4 5 6
7 8 10
1 2 3
4 5 6
7 8 10
Комплексные числа
Комплексные числа имеют как действительную, так и мнимую части, где мнимая единица представляет собой квадратный корень из -1 .
Для представления мнимой части комплексных чисел используйте i или j .
c = [3 + 4i, 4 + 3j; -i, 10j]
c = 2 × 2 комплекс 3.0000 + 4.0000i 4.0000 + 3.0000i 0,0000 - 1,0000i 0,0000 + 10,0000i
Форматирование матрицы — Руководство пользователя CVXOPT
В этом приложении описаны способы настройки форматирования матриц CVXOPT.
Как и другие объекты Python, функции repr и str возвращать строки с печатными представлениями матриц. Команда
« print A » выполняет « str (A) », тогда как команда « A »
называет « repr (A) ».В следующем примере показано значение по умолчанию
форматирование плотных матриц.
>>> из матрицы импорта cvxopt >>> A = матрица (диапазон (50), (5,10), 'd') >>> А <Матрица 5x10, tc = 'd'> >>> print (A) [0.00e + 00 5.00e + 00 1.00e + 01 1.50e + 01 2.00e + 01 2.50e + 01 3.00e + 01 ...] [1.00e + 00 6.00e + 00 1.10e + 01 1.60e + 01 2.10e + 01 2.60e + 01 3.10e + 01 ...] [2.00e + 00 7.00e + 00 1.20e + 01 1.70e + 01 2.20e + 01 2.70e + 01 3.20e + 01 ...] [3.00e + 00 8.00e + 00 1.30e + 01 1.80e + 01 2.30e + 01 2.80e + 01 3.30e + 01 ...] [4.00e + 00 9.00e + 00 1.40e + 01 1.90e + 01 2.40e + 01 2.90e + 01 3.40e + 01 ...]
Формат параметризуется с помощью словаря опции в
модуль cvxopt.. Параметры 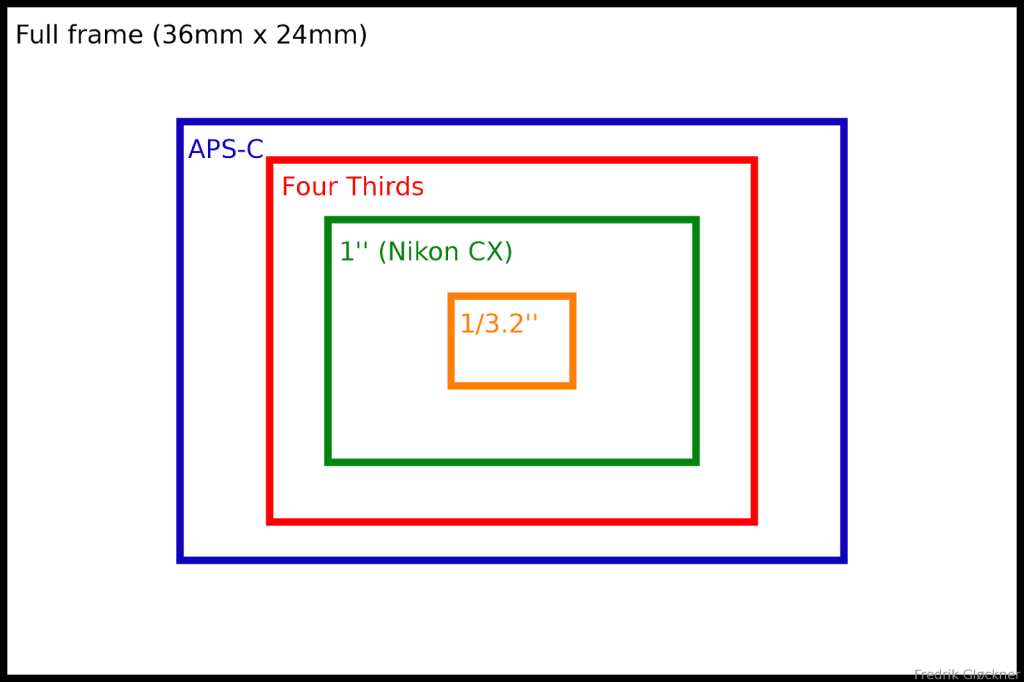 printing
printing options ['iformat'] и options ['dformat'] определяют, соответственно, как integer и
печатаются двойные / комплексные числа. Записи представляют собой строки формата Python
со значениями по умолчанию '% .2e' для 'd' и 'z' матриц и % i ' для матриц ' i '.Параметры
Параметры ['ширина'] Параметры и ['высота'] указывают максимальное
количество отображаемых столбцов и строк. Если options ['width'] равно
установлено отрицательное значение, отображаются все столбцы. Если options ['height'] имеет отрицательное значение, все строки
отображается. Значения по умолчанию options ['width'] и options ['height'] равны 7 и -1 соответственно.
>>> из cvxopt import print
>>> печать.опции
{'width': 7, 'dformat': '% .2e', 'iformat': '% i', 'height': -1}
>>> Printing.options ['dformat'] = '% . 1f'
>>> Printing.options ['width'] = -1
>>> print (A)
[0,0 5,0 10,0 15,0 20,0 25,0 30,0 35,0 40,0 45,0]
[1,0 6,0 11,0 16,0 21,0 26,0 31,0 36,0 41,0 46,0]
[2,0 7,0 12,0 17,0 22,0 27,0 32,0 37,0 42,0 47,0]
[3,0 8,0 13,0 18,0 23,0 28,0 33,0 38,0 43,0 48,0]
[4,0 9,0 14,0 19,0 24,0 29,0 34,0 39,0 44,0 49,0]
1f'
>>> Printing.options ['width'] = -1
>>> print (A)
[0,0 5,0 10,0 15,0 20,0 25,0 30,0 35,0 40,0 45,0]
[1,0 6,0 11,0 16,0 21,0 26,0 31,0 36,0 41,0 46,0]
[2,0 7,0 12,0 17,0 22,0 27,0 32,0 37,0 42,0 47,0]
[3,0 8,0 13,0 18,0 23,0 28,0 33,0 38,0 43,0 48,0]
[4,0 9,0 14,0 19,0 24,0 29,0 34,0 39,0 44,0 49,0]
Для создания встроенных функций Python repr и str доступны для дальнейшей настройки, в
CVXOPT.Функция cvxopt.matrix_repr используется, когда repr вызывается с аргументом матрицы; и cvxopt.matrix_str используется, когда str вызывается с матрицей
аргумент. По умолчанию функции установлены на Printing.matrix_repr_default и Printing.matrix_str_default соответственно, но они могут быть
переопределен на любые другие функции Python. Например, если мы предпочитаем A , чтобы вернуть тот же результат, что и print A , мы можем просто
переопределить cvxopt., как показано ниже. matrix_repr
matrix_repr
>>> импорт cvxopt >>> из матрицы импорта cvxopt, печать >>> A = матрица (диапазон (4), (2,2), 'd') >>> А <Матрица 2x2, tc = 'd'> >>> cvxopt.matrix_repr = Printing.matrix_str_default >>> А [0.00e + 00 2.00e + 00] [1.00e + 00 3.00e + 00]
Форматирование для разреженных матриц аналогично. Функции repr и str для разреженных матриц — cvxopt.spmatrix_repr и cvxopt.spmatrix_str соответственно. По умолчанию они установлены на Printing.spmatrix_repr_default и print.spmatrix_repr_str .
>>> импорт cvxopt >>> из cvxopt import print, spmatrix >>> A = spmatrix (диапазон (5), диапазон (5), диапазон (5), (5,10)) >>> А <5x10 разреженная матрица, tc = 'd', nnz = 5> >>> print (A) [0.00e + 00 0 0 0 0 0 0 ...] [0 1.00e + 00 0 0 0 0 0...] [0 0 2.00e + 00 0 0 0 0 ...] [0 0 0 3.00e + 00 0 0 0 ...] [0 0 0 0 4.00e + 00 0 0 ...]
>>> cvxopt.spmatrix_repr = Printing.spmatrix_str_default >>> А [0.00e + 00 0 0 0 0 0 0 ...] [0 1.00e + 00 0 0 0 0 0 ...] [0 0 2.00e + 00 0 0 0 0 ...] [0 0 0 3.00e + 00 0 0 0 ...] [0 0 0 0 4.00e + 00 0 0 ...]
Как видно из примера, поведение по умолчанию — распечатать
вся матрица, включая структурные нули. Альтернативная тройная печать
стиль определен в файле Printing.spmatrix_str_triplet .
>>> cvxopt.spmatrix_str = Printing.spmatrix_str_triplet >>> print (A) (0,0) 0.00e + 00 (1,1) 1.00e + 00 (2,2) 2.00e + 00 (3,3) 3.00e + 00 (4,4) 4.00e + 00
Формат файлов Matrix Market
Формат файла Matrix MarketКод и библиотеки
Код для чтения и анализа графиков в формате mtx (как и во многих других форматах графиков):
Обратите внимание, что считыватели графиков в PMC и PGD довольно надежны и во многих случаях способны читать и определять тип формата графика. Кроме того, считыватели mtx в этих библиотеках могут читать файлы mtx, которые могут нарушать одну или несколько характеристик файла MTX.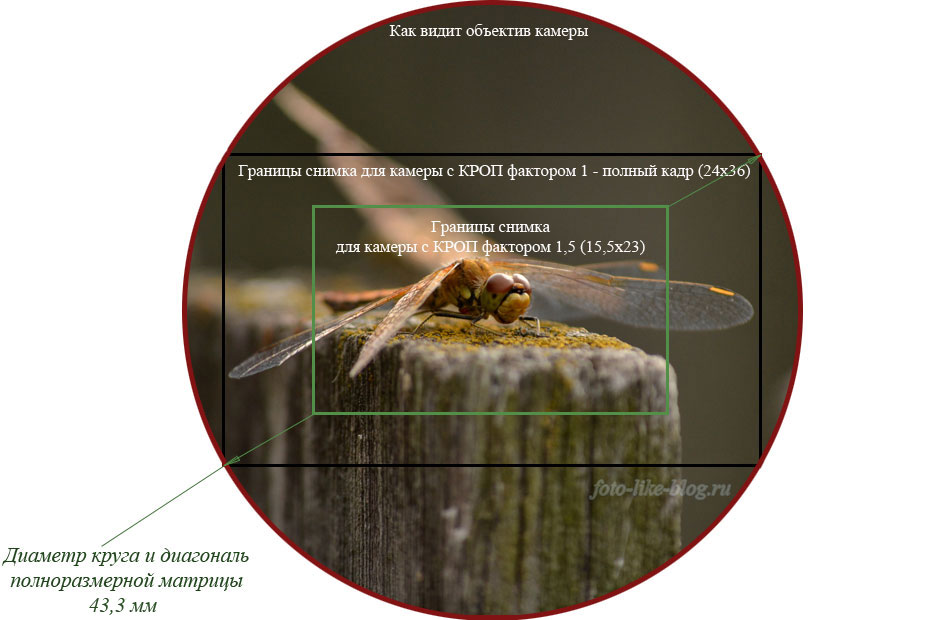
Комментарии к примечаниям обозначаются как минимум одним % .
Строка заголовка обычно является первой строкой, которая начинается по крайней мере с одного % и во многих случаях двух %% , за которым следует MatrixMarket и в большинстве случаев четыре поля, которые описывают сохраненные данные.
Как правило, первая строка без % представляет N M K , где N — количество строк, M — количество столбцов, а K — количество ненулевых значений в матрице.Для неориентированных графов первая строка без % представляет N N M , где N — количество узлов, а M — количество ребер. Например, первая строка выше — 4 4 6 и указывает, что количество узлов равно N = 4, а количество ребер — M = 6.
Графический файл с расширением .mtx читается (PGD и PMC выше) с помощью этого (в некоторой степени) строгого считывателя графов mtx.
Таким образом, если файл графика не соответствует указанному выше формату mtx (например,g. , если граф является списком ребер, без строки заголовка или строки, которая кодирует количество строк, столбцов и ненулевых значений,
затем следует изменить расширение файла, чтобы он мог быть прочитан более гибким средством чтения графиков, обсуждаемым ниже.
, если граф является списком ребер, без строки заголовка или строки, которая кодирует количество строк, столбцов и ненулевых значений,
затем следует изменить расширение файла, чтобы он мог быть прочитан более гибким средством чтения графиков, обсуждаемым ниже.
Список краев: Эти коды разработаны так, чтобы быть максимально гибкими и допускать множество вариантов списков краев. Обратите внимание, что эти коды могут быть немного медленнее, чем считыватель mtx. Это связано с возможностью гибких форматов списков краев. Следовательно, этот считыватель должен выполнить множество проверок, чтобы выяснить точный формат входного файла, и выполнить любую необходимую предварительную обработку, которая может потребоваться.
Разделители: считыватель принимает списки краев, разделенные запятыми, пробелами или табуляцией.
Комментарии: Комментарии разрешены и должны быть обозначены первым символом новой строки как # или%
Веса: Если список ребер содержит веса в 3-м столбце, они просто игнорируются.
 Пользователь может указать считывать веса, установив параметр wt или отметив, что график фактически является временным графиком.
Пользователь может указать считывать веса, установив параметр wt или отметив, что график фактически является временным графиком.Мультиграф: Когда список ребер содержит несколько ребер, мы просто удаляем повторяющиеся ребра.
Список ребер может также содержать пробелы в идентификаторах вершин (непоследовательные идентификаторы вершин) и начинаться с любого положительного целого числа. Самостоятельные петли убираются.
Предполагается, что список ребер неориентирован. Однако если задан ориентированный граф, он просто считается неориентированным.
Формат файла MM / MTX
- Формат ASCII;
- разрешить строки комментариев, которые начинаются со знака процента;
- используйте «координатный» формат для разреженных матриц;
- используйте формат «массив» для общих плотных матриц;
Файл в формате Matrix Market состоит из четырех частей:
- Строка заголовка: содержит идентификатор и четыре текстовых поля;
- Строки комментариев: позволяют пользователю сохранять информацию и комментарии;
- Строка размера: указывает количество строк и столбцов, и количество ненулевых элементов;
- Строки данных: определяют расположение записей матрицы
(неявно или явно) и их значения.

Строка заголовка имеет вид
% MatrixMarket объект формат поле симметрия или
% MatrixMarket объект формат поле симметрия Строка заголовка должна быть первой строкой файла, а заголовок строка должна начинаться со строки % MatrixMarket или %% MatrixMarket .Четверка поля, следующие за этой строкой,
- объект обычно представляет собой матрицу , и это случай мы рассмотрим здесь. Еще одно юридическое значение вектор , формат которого аналогичен, но с некоторыми очевидные упрощения.
- формат — это либо координата , либо массив ;
- поле либо вещественное , двойное , сложное , целое число или шаблон .

- симметрия либо общий (законный для реального, сложного, целочисленные поля или поля шаблона), симметричный (действительный, комплексный, целочисленный или шаблонный), кососимметричный (действительный, комплексный или целочисленный), или эрмитский (только комплекс).
Если поле матрицы представляет собой образец , то будут перечислены только местоположения ненулевых значений.Этот предполагает, очевидно, что мы используем координату формат!
Если симметрия матрицы равна симметрии или hermitian , то только записи на или под указывается главная диагональ. Если симметрия кососимметричный , то только записи строго под главной диагональю должны быть указаны.
Строки комментариев, если таковые имеются, должны следовать за строкой заголовка. Единственное требование — каждая строка комментария должна начинаться с
знак процента.
Единственное требование — каждая строка комментария должна начинаться с
знак процента.
Если формат был задан как массив , то Линия размера имеет вид:
м н
куда- м — количество строк в матрице;
- n — количество столбцов в матрице;
Если формат был указан как координата , то Линия размера имеет вид:
m n ненулевые
куда- м — количество строк в матрице;
- n — количество столбцов в матрице;
- ненулевых — количество ненулевых элементов в матрице
(для общей симметрии), или количество ненулевых элементов
на диагонали или ниже (для симметричной или эрмитовой симметрии),
или количество ненулевых элементов ниже диагонали (для
кососимметричная симметрия).

Если формат был задан как массив , то должен быть точно следовать м * n строки данных, одна для каждая запись, перечисленная по столбцам, имеет форму
значение
куда- значение — это значение записи. Если поле — комплексный , требуется пара действительных чисел.
Если формат был указан как координата , то должно быть следуйте точно ненулевым строкам данных, одна для каждая запись матрицы, которая должна быть указана, имеет вид
i j значение
куда- i — строка записи;
- j — столбец записи;
- значение — это значение записи.Если поле — комплексный , требуется пара действительных чисел.
 Если
значение формата было шаблон , тогда значение не
перечислено здесь; встречаются только значения i и j .
Если
значение формата было шаблон , тогда значение не
перечислено здесь; встречаются только значения i и j .
Разреженные матрицы (scipy.sparse) — SciPy v1.6.1 Справочное руководство
SciPy 2-D пакет разреженных матриц для числовых данных.
Содержание
Классы разреженных матриц
| Матрица блоков разреженных строк |
| Разреженная матрица в формате COOrdinate. |
| Сжатая матрица с разреженными столбцами |
| Сжатая матрица разреженных строк |
| Разреженная матрица с DIAgonal хранилищем |
| Разреженная матрица на основе словаря ключей. |
| Построчный список списков разреженная матрица |
| Этот класс предоставляет базовый класс для всех разреженных матриц. |
Функции
Построение разреженных матриц:
| Разреженная матрица с матрицами по диагонали |
| Матрица идентичности в разреженном формате |
| произведение кронекера разреженных матриц А и Б |
| сумма кронекера разреженных матриц A и B |
| Постройте разреженную матрицу из диагоналей. |
| Возвращает разреженную матрицу по диагонали. |
| Постройте блочно-диагональную разреженную матрицу из предоставленных матриц. |
| Вернуть нижнюю треугольную часть матрицы в разреженном формате |
| Вернуть верхнюю треугольную часть матрицы в разреженном формате |
| Построить разреженную матрицу из разреженных субблоков |
| Укладывать разреженные матрицы по горизонтали (по столбцам) |
| Укладывать разреженные матрицы вертикально (по строкам) |
| Создает разреженную матрицу заданной формы и плотности с равномерно распределенными значениями. |
| Создает разреженную матрицу заданной формы и плотности со случайно распределенными значениями. |
Сохранение и загрузка разреженных матриц:
| Сохранение разреженной матрицы в файл в формате |
| Загрузить разреженную матрицу из файла в формате |
Инструменты для разреженной матрицы:
| Возвращает индексы и значения ненулевых элементов матрицы |
Определение разреженных матриц:
Информация об использовании
Доступно семь типов разреженных матриц:
csc_matrix: формат сжатого разреженного столбца
csr_matrix: формат сжатой разреженной строки
bsr_matrix: Формат разреженных строк блока
lil_matrix: Формат списка списков
dok_matrix: Формат словаря ключей
coo_matrix: COOrdinate формат (также известный как IJV, триплетный формат)
dia_matrix: DIA Угловой формат
Для эффективного построения матрицы используйте dok_matrix или lil_matrix. Класс lil_matrix поддерживает базовую нарезку и причудливую индексацию с
аналогичный синтаксис массивам NumPy. Как показано ниже, формат COO
также может использоваться для эффективного построения матриц. Несмотря на их
сходство с массивами NumPy, настоятельно не рекомендуется, использовать NumPy
работает непосредственно с этими матрицами, потому что NumPy может неправильно преобразовать
их для вычислений, приводящих к неожиданным (и неверным) результатам. если ты
хотите применить функцию NumPy к этим матрицам, сначала проверьте, есть ли в SciPy
собственная реализация для данного класса разреженных матриц, или преобразует
разреженная матрица в массив NumPy (e.g., используя метод toarray () объекта
class) перед применением метода.
Класс lil_matrix поддерживает базовую нарезку и причудливую индексацию с
аналогичный синтаксис массивам NumPy. Как показано ниже, формат COO
также может использоваться для эффективного построения матриц. Несмотря на их
сходство с массивами NumPy, настоятельно не рекомендуется, использовать NumPy
работает непосредственно с этими матрицами, потому что NumPy может неправильно преобразовать
их для вычислений, приводящих к неожиданным (и неверным) результатам. если ты
хотите применить функцию NumPy к этим матрицам, сначала проверьте, есть ли в SciPy
собственная реализация для данного класса разреженных матриц, или преобразует
разреженная матрица в массив NumPy (e.g., используя метод toarray () объекта
class) перед применением метода.
Для выполнения таких операций, как умножение или инверсия, сначала
преобразовать матрицу в формат CSC или CSR. Формат lil_matrix:
на основе строк, поэтому преобразование в CSR эффективно, тогда как преобразование в CSC
меньше так.
Все преобразования между форматами CSR, CSC и COO эффективны, операции с линейным временем.
Матрица векторного произведения
Чтобы произвести векторное произведение между разреженной матрицей и вектором, просто используйте метод matrix dot , как описано в его строке документации:
>>> импортировать numpy как np >>> от scipy.разреженный импорт csr_matrix >>> A = csr_matrix ([[1, 2, 0], [0, 0, 3], [4, 0, 5]]) >>> v = np.array ([1, 0, -1]) >>> A.dot (v) массив ([1, -3, -1], dtype = int64)
Предупреждение
Начиная с NumPy 1.7, np.dot не знает о разреженных матрицах, поэтому его использование приведет к неожиданным результатам или ошибкам. Вместо этого сначала должен быть получен соответствующий плотный массив:
>>> np.dot (A.toarray (), v) массив ([1, -3, -1], dtype = int64)
, но тогда все преимущества в производительности будут потеряны.
Формат CSR особенно подходит для быстрых матричных векторных продуктов.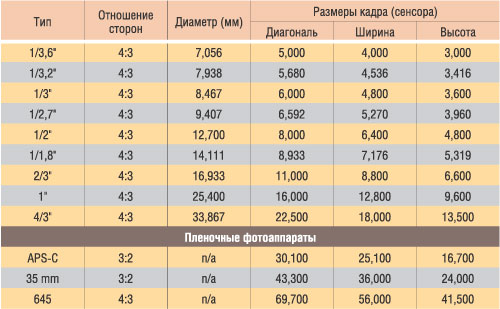
Пример 1
Создайте lil_matrix размером 1000×1000 и добавьте к нему несколько значений:
>>> из scipy.sparse import lil_matrix >>> из scipy.sparse.linalg import spsolve >>> из импорта numpy.linalg решить, норма >>> из numpy.random import rand
>>> A = lil_matrix ((1000, 1000)) >>> A [0,: 100] = rand (100) >>> A [1, 100: 200] = A [0,: 100] >>> А.setdiag (ранд (1000))
Теперь преобразуйте его в формат CSR и решите A x = b для x:
>>> A = A.tocsr () >>> b = rand (1000) >>> x = spsolve (A, b)
Преобразуйте его в плотную матрицу и решите, и убедитесь, что результат то же самое:
>>> x_ = решить (A.toarray (), b)
Теперь мы можем вычислить норму ошибки с помощью:
>>> err = norm (x-x_) >>> эрр <1e-10 Истинный
Он должен быть маленьким 🙂
Пример 2
Построить матрицу в формате COO:
>>> из scipy import sparse >>> из массива импорта numpy >>> I = массив ([0,3,1,0]) >>> J = массив ([0,3,1,2]) >>> V = массив ([4,5,7,9]) >>> А = разреженный.coo_matrix ((V, (I, J)), shape = (4,4))
Обратите внимание, что индексы не нужно сортировать.
Дублирующиеся (i, j) записи суммируются при преобразовании в CSR или CSC.
>>> I = массив ([0,0,1,3,1,0,0]) >>> J = массив ([0,2,1,3,1,0,0]) >>> V = массив ([1,1,1,1,1,1,1]) >>> B = sparse.coo_matrix ((V, (I, J)), shape = (4,4)). Tocsr ()
Это полезно для построения матриц жесткости и массы методом конечных элементов.
Дополнительная информация
Индексы столбцов CSR не обязательно отсортированы.Аналогично для строки CSC индексы. Используйте методы .sorted_indices () и .sort_indices (), когда отсортированные индексы обязательны (например, при передаче данных в другие библиотеки).
Что такое матричная диаграмма или диаграмма? Анализ взаимосвязи данных
Глоссарий качества Определение: Матрица
Также называется: матрица, матричная диаграмма
Матричная диаграмма определяется как новый инструмент планирования управления, используемый для анализа и отображения взаимосвязи между наборами данных. Матричная диаграмма показывает взаимосвязь между двумя, тремя или четырьмя группами информации. Он также может дать информацию о взаимосвязи, например, о ее силе, о ролях, которые играют разные люди или измерения.
Матричная диаграмма показывает взаимосвязь между двумя, тремя или четырьмя группами информации. Он также может дать информацию о взаимосвязи, например, о ее силе, о ролях, которые играют разные люди или измерения.
Возможны шесть матриц различной формы: L, T, Y, X, C и в форме крыши, в зависимости от того, сколько групп необходимо сравнить.
Когда использовать каждую форму матричной диаграммы
Таблица 1 показывает, когда использовать каждый тип матрицы. Щелкните по ссылкам ниже, чтобы увидеть примеры каждого типа.В примерах оси матриц заштрихованы, чтобы выделить букву, дающую имя каждой матрице.
- L-образная матрица связывает две группы элементов друг с другом (или одну группу с собой).
- Т-образная матрица связывает три группы элементов: каждая из групп B и C связана с A; группы B и C не связаны друг с другом.
- Y-образная матрица связывает три группы элементов: каждая группа связана с двумя другими по кругу.
- C-образная матрица связывает три группы элементов одновременно в 3D.

- X-образная матрица связывает четыре группы элементов: каждая группа связана с двумя другими по кругу.
- Матрица в форме крыши связывает одну группу предметов с собой; обычно используется вместе с L- или T-образной матрицей.
Таблица 1: Когда использовать матрицы другой формы
Г-образная | 2 группы | A B (или A A) |
Т-образный | 3 группы | B A C, но не B C |
Y-образная | 3 группы | A B C A |
C-образная | 3 группы | Все три одновременно (3D) |
Х-образная | 4 группы | A B C D A, но не A C или B D |
Крыша | 1 группа | A A, если также A B в L или T |
Эта L-образная матрица суммирует требования клиентов. Команда поместила числа в поля, чтобы показать числовые характеристики, и использовала галочки, чтобы обозначить выбор упаковки. L-образная матрица на самом деле образует перевернутую L. Это самый простой и наиболее распространенный формат матрицы.
Команда поместила числа в поля, чтобы показать числовые характеристики, и использовала галочки, чтобы обозначить выбор упаковки. L-образная матрица на самом деле образует перевернутую L. Это самый простой и наиболее распространенный формат матрицы.
L-образная матричная диаграмма: требования клиентов
Заказчик | Заказчик | Клиент | Клиент | |
Чистота% | > 99.2 | > 99,2 | > 99,4 | > 99,0 |
Следы металлов (ppm) | <5 | – | <10 | <25 |
Вода (ppm) | <10 | <5 | <10 | – |
Вязкость (сП) | 20-35 | 20-30 | 10-50 | 15-35 |
Цвет | <10 | <10 | <15 | <10 |
Барабан | ||||
Грузовик | ||||
| Вагон |
Вернуться к началу
Эта Т-образная матрица связывает модели продуктов (группа A) с их производственными площадками (группа B) и их клиентами (группа C).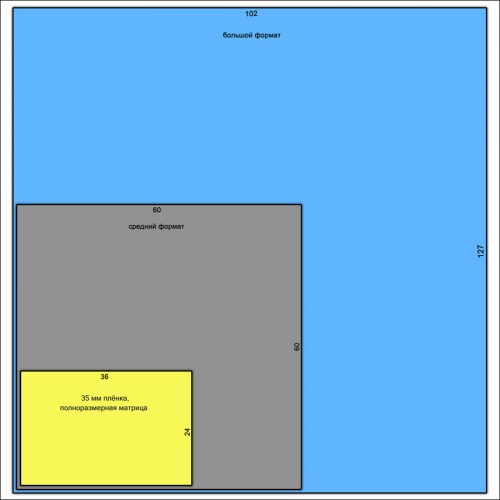
Изучение матрицы (ниже) разными способами дает разную информацию. Например, если сосредоточиться на модели A, видно, что она производится в больших объемах на заводе в Техасе и в небольших объемах на заводе в Алабаме. Time Inc. является основным покупателем модели A, в то время как Arlo Co. покупает небольшую сумму. Сосредоточение внимания на рядах покупателей показывает, что только один покупатель, Arlo Co., покупает все четыре модели. Zig Corp. покупает только одну. Time Inc. делает крупные покупки A и D, в то время как Lyle Co. является относительно незначительным клиентом.
Т-образная матричная диаграмма: продукты - производственные предприятия - Клиенты
Вернуться к началу
Эта Y-образная матрица показывает отношения между требованиями клиентов, метриками внутренних процессов и задействованными отделами. Символы показывают силу взаимоотношений: основные взаимоотношения, такие как ответственность производственного отдела за производственные мощности; вторичные отношения, такие как связь между доступностью продукта и уровнями запасов; второстепенные отношения, такие как ответственность отдела сбыта за время выполнения заказа; и никаких отношений, например, между отделом закупок и своевременной доставкой.
Y-образная матричная диаграмма: ответственность за выполнение требований клиентов
Вернуться к началу
Поскольку эта матрица трехмерна, ее трудно рисовать и она используется нечасто. Если важно сравнить три группы одновременно, рассмотрите возможность использования трехмерной модели или компьютерного программного обеспечения, которое может обеспечить четкое визуальное изображение.
С-образная матричная диаграмма
Вернуться к началу
На этом рисунке пример Т-образной матрицы расширен до Х-образной матрицы, включая отношения грузовых линий с производственными площадками, которые они обслуживают, и клиентами, которые их используют.Каждая ось матрицы связана с двумя соседними, но не с одной поперечной. Таким образом, модели продуктов связаны с производственными площадками и клиентами, но не с грузовыми линиями.
X-образная матричная диаграмма: производственные площадки - продукты - клиенты - грузовые линии
Вернуться к началу
Матрица в форме крыши используется с L- или T-образной матрицей для отображения одной группы элементов, относящихся к самой себе. Чаще всего он используется с Домом качества, где образует «крышу» дома.«На приведенном ниже рисунке требования клиентов связаны друг с другом. Например, сильная взаимосвязь связывает цвет и следы металлов, в то время как вязкость не связана ни с одним из других требований.
Чаще всего он используется с Домом качества, где образует «крышу» дома.«На приведенном ниже рисунке требования клиентов связаны друг с другом. Например, сильная взаимосвязь связывает цвет и следы металлов, в то время как вязкость не связана ни с одним из других требований.
Матричная диаграмма в форме крыши
Часто используемые символы матричных диаграмм
Вернуться к началу
Адаптировано из The Quality Toolbox, Second Edition , ASQ Quality Press.
.
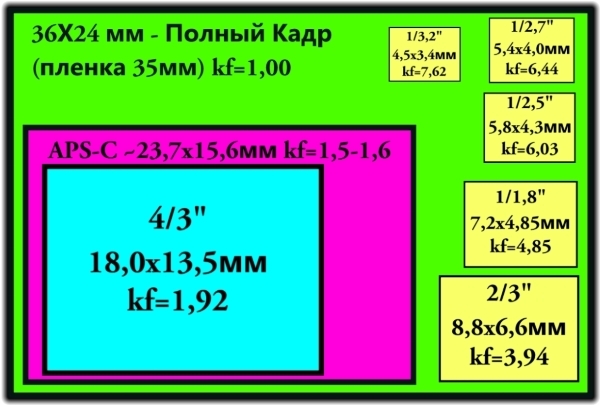 2″ – самые маленькие матрицы, соотношение сторон 4:3, физический размер 3.4 х 4.5 кв.мм;
2″ – самые маленькие матрицы, соотношение сторон 4:3, физический размер 3.4 х 4.5 кв.мм;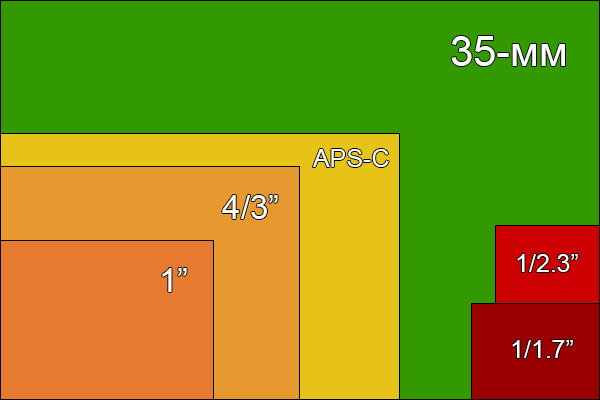 КМОП-матрица – это комплиментарный металл-оксид-полупроводник. Данная технология позволяет производить выборку отдельного пикселя почти так же, как и в стандартной системе памяти, к тому же, каждый пиксель оснащается дополнительным усилителем. Поскольку данная система является более современной, она зачастую оснащается автоматической подстройкой времени экспонирования каждого пикселя по отдельности. Данное улучшение позволяет получить полный кадр без потери боковых границ, а так же без потери верха и низа кадра. Полноразмерная матрица чаще всего бывает выполнена по технологии КМОП.
КМОП-матрица – это комплиментарный металл-оксид-полупроводник. Данная технология позволяет производить выборку отдельного пикселя почти так же, как и в стандартной системе памяти, к тому же, каждый пиксель оснащается дополнительным усилителем. Поскольку данная система является более современной, она зачастую оснащается автоматической подстройкой времени экспонирования каждого пикселя по отдельности. Данное улучшение позволяет получить полный кадр без потери боковых границ, а так же без потери верха и низа кадра. Полноразмерная матрица чаще всего бывает выполнена по технологии КМОП. Разумеется, чем этот параметр будет больше, тем лучший снимок получится сделать.
Разумеется, чем этот параметр будет больше, тем лучший снимок получится сделать. Она осуществляется при помощи специальных щеточек, одна из которых влажная, другая сухая. Этот вид уборки нужен для пылинок, которые, будучи мокрыми, попали на поверхность стекла, и, высохнув, прикрепились к нему, создав эффект «битого пикселя». Влажная щетка пропитана специальным раствором, который эффективно удаляет засохшие песчинки и пылинки, не оставляя пятен и разводов. Необходимо проводить по стеклу плавными аккуратными движениями, лишь слегка нажимая на саму щетку. Оставшаяся влага довольно быстро испарится сама. Даже если после влажной уборки на стекле остается пара капель, то они прекрасно удаляются сухой щеточкой (кисточкой).
Она осуществляется при помощи специальных щеточек, одна из которых влажная, другая сухая. Этот вид уборки нужен для пылинок, которые, будучи мокрыми, попали на поверхность стекла, и, высохнув, прикрепились к нему, создав эффект «битого пикселя». Влажная щетка пропитана специальным раствором, который эффективно удаляет засохшие песчинки и пылинки, не оставляя пятен и разводов. Необходимо проводить по стеклу плавными аккуратными движениями, лишь слегка нажимая на саму щетку. Оставшаяся влага довольно быстро испарится сама. Даже если после влажной уборки на стекле остается пара капель, то они прекрасно удаляются сухой щеточкой (кисточкой).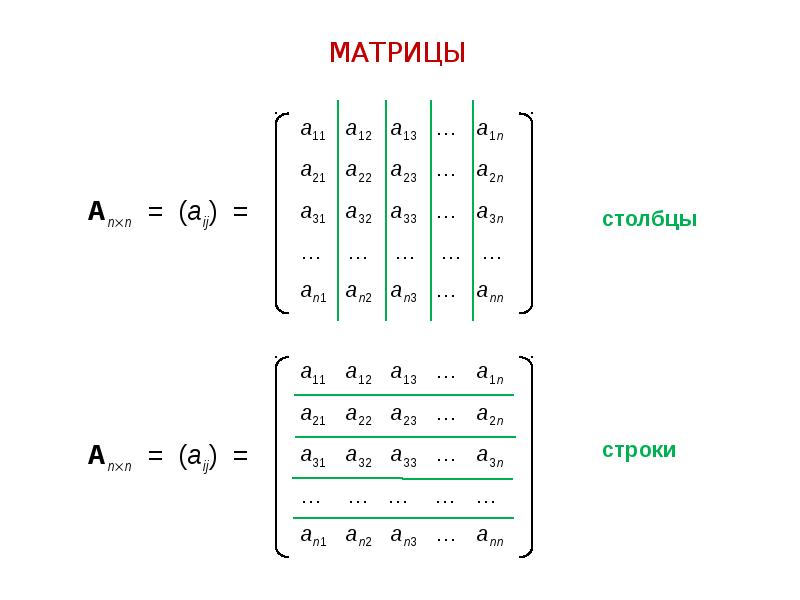 0 -0,1 1,0
Ряд-B 3,0 0,0 8,0
Ряд-C 0,2 0,1 2,5
0 -0,1 1,0
Ряд-B 3,0 0,0 8,0
Ряд-C 0,2 0,1 2,5
 000000000000000 0 0
0,000000000000002 1,00000000000000000 0
0.000000000000002 -0.000000000000004 1.000000000000000
000000000000000 0 0
0,000000000000002 1,00000000000000000 0
0.000000000000002 -0.000000000000004 1.000000000000000
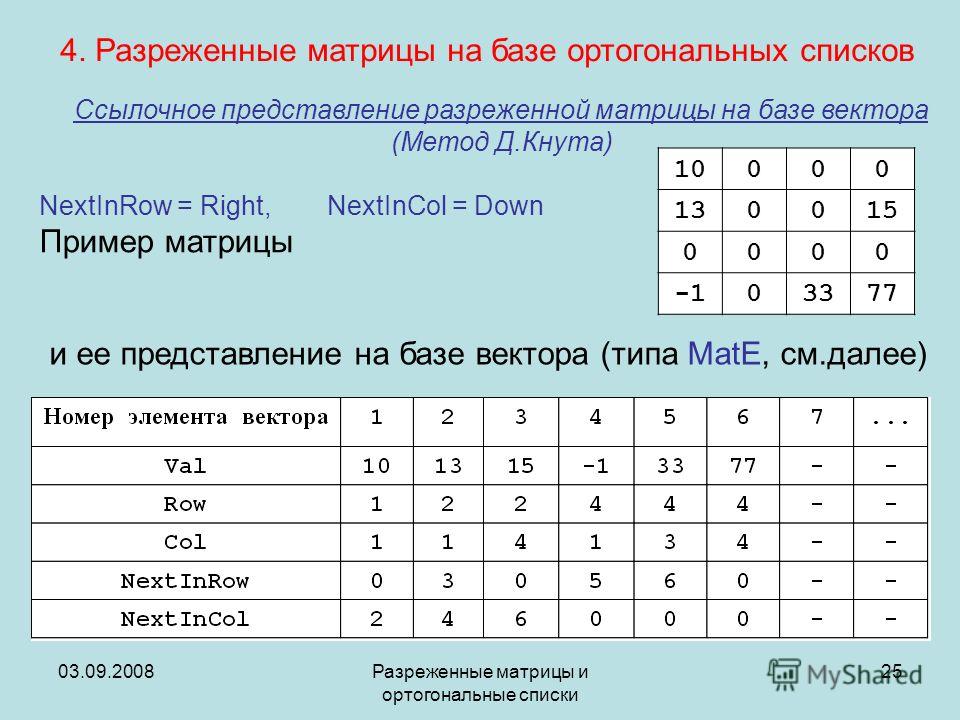 1f'
>>> Printing.options ['width'] = -1
>>> print (A)
[0,0 5,0 10,0 15,0 20,0 25,0 30,0 35,0 40,0 45,0]
[1,0 6,0 11,0 16,0 21,0 26,0 31,0 36,0 41,0 46,0]
[2,0 7,0 12,0 17,0 22,0 27,0 32,0 37,0 42,0 47,0]
[3,0 8,0 13,0 18,0 23,0 28,0 33,0 38,0 43,0 48,0]
[4,0 9,0 14,0 19,0 24,0 29,0 34,0 39,0 44,0 49,0]
1f'
>>> Printing.options ['width'] = -1
>>> print (A)
[0,0 5,0 10,0 15,0 20,0 25,0 30,0 35,0 40,0 45,0]
[1,0 6,0 11,0 16,0 21,0 26,0 31,0 36,0 41,0 46,0]
[2,0 7,0 12,0 17,0 22,0 27,0 32,0 37,0 42,0 47,0]
[3,0 8,0 13,0 18,0 23,0 28,0 33,0 38,0 43,0 48,0]
[4,0 9,0 14,0 19,0 24,0 29,0 34,0 39,0 44,0 49,0]
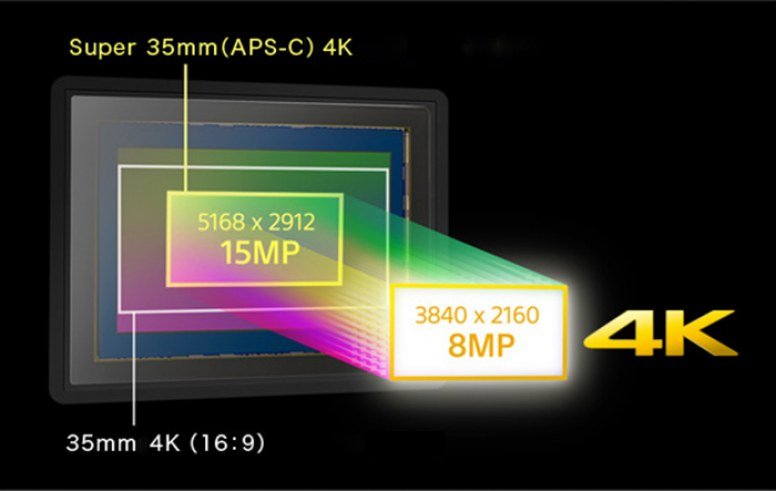 spmatrix_repr = Printing.spmatrix_str_default
>>> А
[0.00e + 00 0 0 0 0 0 0 ...]
[0 1.00e + 00 0 0 0 0 0 ...]
[0 0 2.00e + 00 0 0 0 0 ...]
[0 0 0 3.00e + 00 0 0 0 ...]
[0 0 0 0 4.00e + 00 0 0 ...]
spmatrix_repr = Printing.spmatrix_str_default
>>> А
[0.00e + 00 0 0 0 0 0 0 ...]
[0 1.00e + 00 0 0 0 0 0 ...]
[0 0 2.00e + 00 0 0 0 0 ...]
[0 0 0 3.00e + 00 0 0 0 ...]
[0 0 0 0 4.00e + 00 0 0 ...]
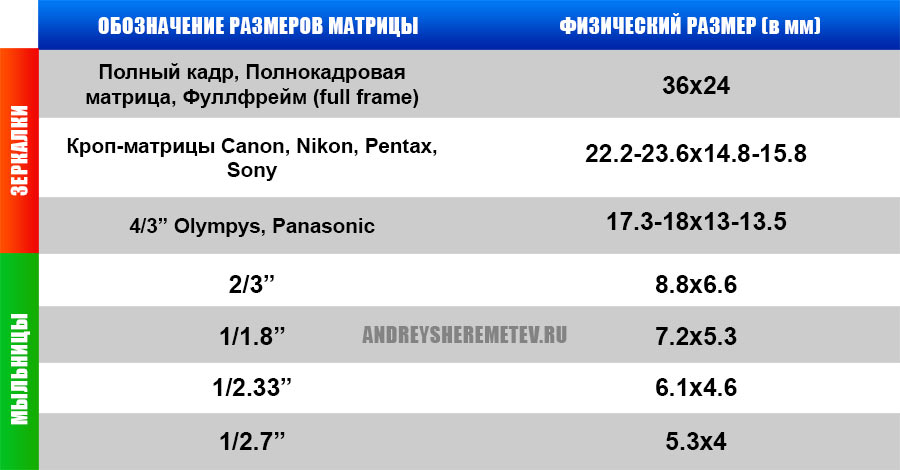 Пользователь может указать считывать веса, установив параметр wt или отметив, что график фактически является временным графиком.
Пользователь может указать считывать веса, установив параметр wt или отметив, что график фактически является временным графиком.
 Если
значение формата было шаблон , тогда значение не
перечислено здесь; встречаются только значения i и j .
Если
значение формата было шаблон , тогда значение не
перечислено здесь; встречаются только значения i и j .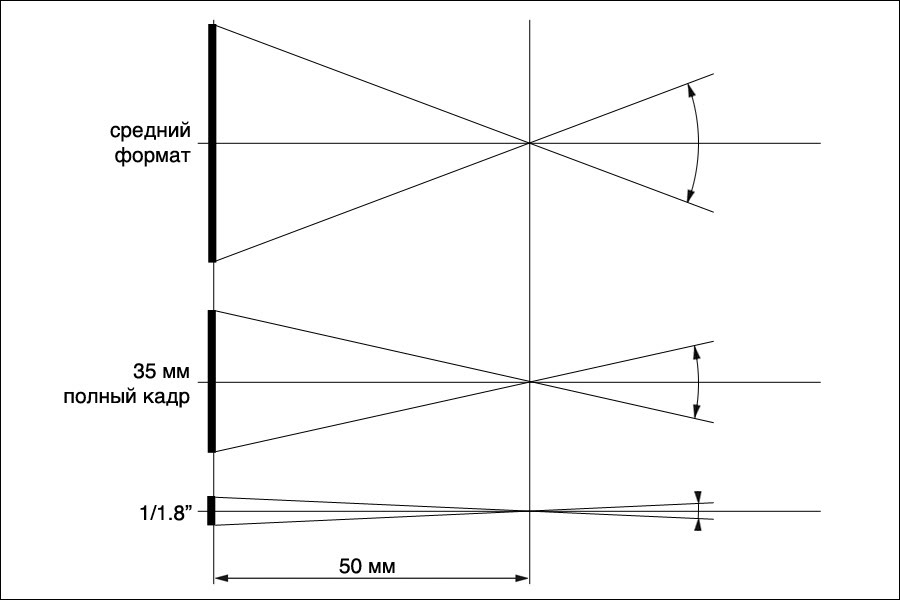
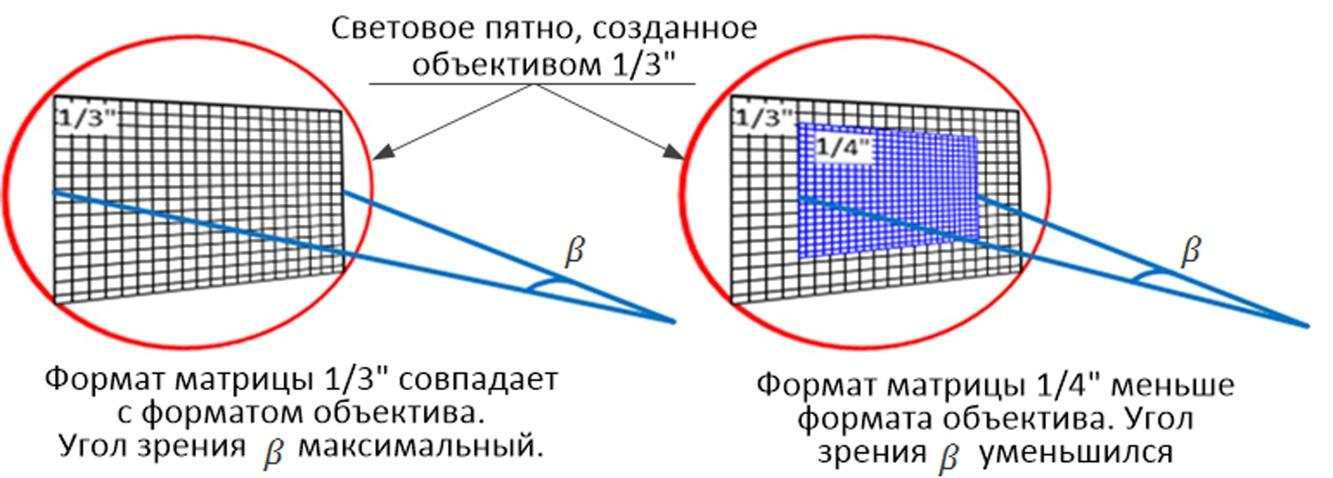

 coo_matrix ((V, (I, J)), shape = (4,4))
coo_matrix ((V, (I, J)), shape = (4,4))
