Золотое сечение — что это такое? Числа Фибоначчи — это?
Автор Алёна Краева На чтение 3 мин. Опубликовано
Здравствуйте, дорогие читатели!
Золотое сечение — что это такое? Числа Фибоначчи — это? В статье — ответы на эти вопросы кратно и понятно, простыми словами.
Эти вопросы вот уже несколько тысячелетий будоражат умы всё новых и новых поколений! Оказывается математика может быть не скучной, а захватывающей, интересной, завораживающей!
Другие полезные статьи: Квантовая физика и сознание человека В чем смысл жизни человека? Объясняет философ Виктор Франкл Как правильно жить? Мудрые советы древнегреческих философов Самопознание или как познать тайны мироздания?
Числа Фибоначчи — это что?
Поразителен тот факт, что при делении каждого последующего числа числовой последовательности на предыдущее получается число, стремящееся к 1,618.
Обнаружил эту загадочную последовательность счастливчик математик средневековья Леонардо Пизанский (более известный под именем Фибоначчи). До него Леонардо да Винчи обнаружил в строении тела человека, растений и животных удивительным образом повторяющуюся пропорцию Фи = 1,618. Это число (1,61) ученые еще называют «Числом Бога».
До Леонардо да Винчи эта последовательность чисел была известна в Древней Индии и Древнем Египте. Египетские пирамиды построены с применением пропорции Фи = 1,618.
Но и это еще не все, оказывается законы природы Земли и Космоса каким-то необъяснимым образом подчиняются строгим математическим законам последовательности чисел Фидоначчи.
Например, и ракушка на Земле, и галактика в Космосе построены с применением чисел Фибоначчи. Абсолютное большинство цветов имеет 5, 8, 13 лепестков. В подсолнухе, на стеблях растений, в закрученных вихрях облаков, в водоворотах и даже в графиках изменения курсов валют на Форексе, всюду работают числа Фибоначчи.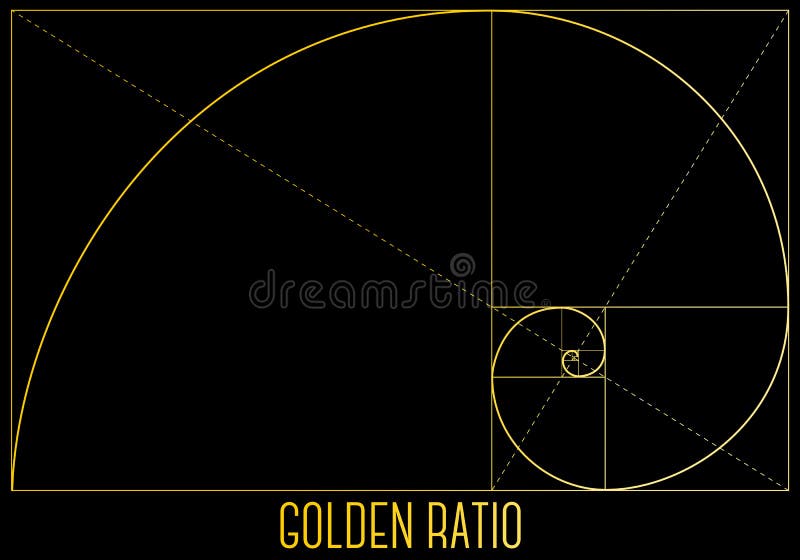
- Посмотрите простое и занимательное пояснение, что такое последовательность чисел Фибоначчи и Золотое сечение в этом КОРОТКОМ ВИДЕО (6 минут):
Что такое Золотое сечение или Божественная пропорция?
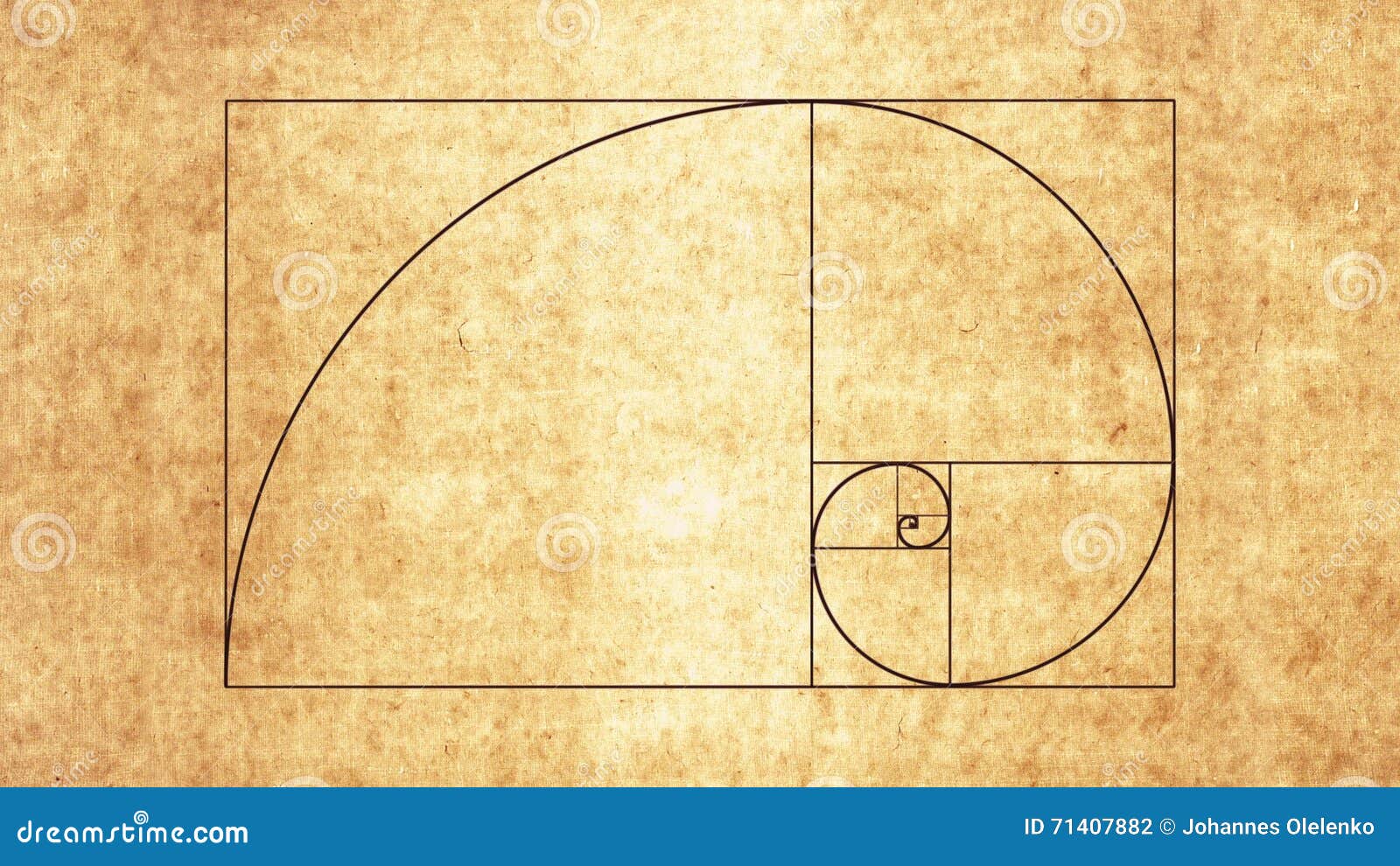
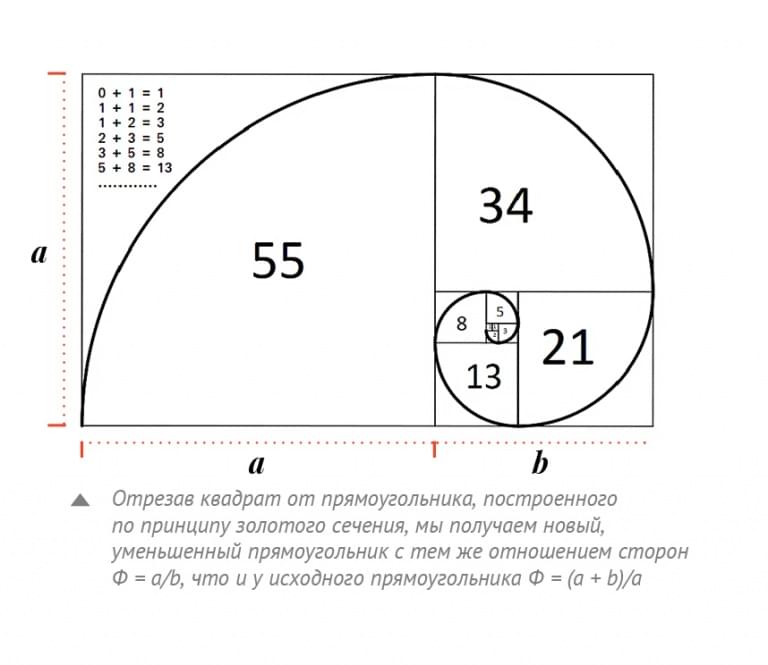
Итак, что такое Золотое сечение или Золотая или Божественная пропорция? Фибоначчи также обнаружил, что последовательность, которая состоит из квадратов чисел Фибоначчи является еще большей загадкой. Попробуем графически изобразить в виде площади последовательность:
1², 2², 3², 5², 8²…
Если вписать спираль в графическое изображение последовательности квадратов чисел Фибоначчи, то мы получим Золотое сечение, по правилам которого построено все во вселенной, включая растения, животных, спираль ДНК, человеческое тело, … Список этот можно продолжать до бесконечности.

Золотое сечение и Числа Фибоначчи в природе ВИДЕО
Предлагаю посмотреть короткий фильм (7 минут), в котором раскрываются некоторые загадки Золотого сечения. При размышлениях о законе чисел Фибоначчи, как о первостепенном законе, который управляет живой и неживой природой, появляется вопрос: Эта идеальная формула для макромира и микромира возникла сама или ее кто-то создал и удачно применил?Что ВЫ думаете по этому поводу? Давайте вместе подумаем над этой загадкой и быть может мы приблизимся к тайне мироздания.
Очень надеюсь, что статья была полезной для Вас и Вы узнали, что это такое Золотое сечение *и Числа Фибоначчи? До новых встреч на страницах блога, подписывайтесь на блог.
Не могу не поделиться с Вами коротким документальным фильмом — ученые обнаружили загадочную связь между кодом ДНК и числом Бога. Форма подписки — под статьей.
Форма подписки — под статьей.Всем желаю много новых идей и вдохновения для их реализации!
Алёна Краева
SMARTБЛОГ
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 |
Использование золотого сечения в фотографии для лучшей композиции
Фотография начинается с композиции. То, как вы создаете сцену, является основным строительным блоком для получения хорошей картинки, и одной из композиционных техник, которая всегда была решающей, является Золотое сечение.
Вот что это значит и как вы можете использовать его для немедленного улучшения ваших фотографий.
Что такое золотое сечение?
Допустим, у вас есть линия. Существует математическое правило, которое гласит, что любая линия может быть разделена таким образом, что более длинный сегмент, разделенный на более короткий сегмент, имеет такое же соотношение, что и полная линия, разделенная на более длинный сегмент.
Чтобы выразить это визуально:
Длина линии равна x + y, первый сегмент — x, второй — y. Таким образом, уравнение: х / у = (х + у) / х = 1,6180339887498948420
Это магическое соотношение составляет 1,618 и известно как «золотое сечение» или «божественная пропорция». В математических кругах это специальное число известно как Phi. Но какое это имеет отношение к фотографии?
С точки зрения композиции изображения, вы можете использовать это соотношение, чтобы решить, как разделить ваш кадр. Не помещайте свой предмет прямо в середину; вместо этого, используя горизонт в качестве ориентира, поставьте объект на отметке 1. 618. Сначала это немного сложно понять, но мы собираемся исследовать это более подробно, поэтому не отчаивайтесь, если вы чувствуете себя потерянным прямо сейчас.
618. Сначала это немного сложно понять, но мы собираемся исследовать это более подробно, поэтому не отчаивайтесь, если вы чувствуете себя потерянным прямо сейчас.
Примечание: Вы можете просто обрезать свою фотографию позже обрезки фотографий, обрезки фотографий,
Что такое Фи Грид?
Многие фотографы предпочитают использовать сетку на основе Фи при составлении своих снимков. Естественно, эта техника называется Фи Грид . Это вариация «Правила третей», одного из базовых принципов фотографии.
Правило третей делит фрейм на три строки и три столбца одинакового размера, в результате чего получается 1: 1: 1 по вертикали и 1: 1: 1 по горизонтали. Phi Grid разделяет рамку аналогичным образом, но уменьшает средний ряд и средний столбец в соответствии с золотым соотношением, в результате чего получается 1: 1,618: 1 по вертикали и 1: 1,618: 1 по горизонтали.
Вот быстрое сравнение:
Пересечение линий сетки — это то место, куда естественным образом обращается глаз, поэтому используйте их для выравнивания изображения. Школа цифровой фотографии предлагает пример использования Phi Grid в подробной статье, которую стоит прочитать полностью:
Я выровнял горизонт с верхней линией сетки Фи. По моему мнению, когда вы выравниваете горизонт с сеткой с правилом третей, разделение слишком … очевидно. Я думаю, что это оставило бы слишком много того, что не является предметом на изображении. На этом фото небо и облака — идеальное дополнение к тому, что я пытаюсь передать на фото: церковь внизу справа и знаменитая улица Дюваль слева. Но если небо больше, чем на фотографии, зритель может подумать, что небо на самом деле является объектом.
Спираль Фибоначчи
В геометрии золотое сечение также может быть выражено как определенный тип прямоугольника. Предположим, вы берете линию x + y выше и поворачиваете ее прямоугольником, где ширина равна x, а длина равна x + y.
Если вы разделите площадь этого прямоугольника на ряд квадратов, он образует спираль последовательности Фибоначчи, как демонстрирует LiveScience :
Если вы читали Код Да Винчи , вы знаете последовательность Фибоначчи : вы начинаете с цифры 1, добавляете предыдущее целое число и делаете бесконечный ряд чисел с этим шаблоном. Так что сериал выглядит так:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
Фибоначчи обнаружил, что эта «золотая спираль» появляется в нескольких местах по всей природе, от молекул ДНК до цветочных лепестков, от ураганов до Млечного пути. Что еще более важно, спираль Фибоначчи приятна человеческому глазу.
Адриан Беджан, профессор машиностроения в Школе инженерии имени Пратта при Герцоге, говорит, что золотое сечение эстетически приятно из-за эволюции человеческого зрения.
Короче говоря, наш мозг должен обрабатывать все, что видят наши глаза. Чем быстрее он может что-то обработать, тем приятнее это будет. Любое изображение с золотым сечением обрабатывается мозгом быстрее, поэтому оно посылает сигнал, что такое изображение эстетично.
Любое изображение с золотым сечением обрабатывается мозгом быстрее, поэтому оно посылает сигнал, что такое изображение эстетично.
Как использовать спираль Фибоначчи
С точки зрения реальной фотографии, вам не нужно беспокоиться о технических объяснениях. Спирали Фибоначчи полезны практически для всех видов фотографии, но особенно хороши для пейзажей и широкоформатных снимков.
У Apogee Photo есть отличный пример того, как его использовать:
Осенью был туманный вечер, и я хотел запечатлеть цвета заката, которые проникали сквозь туман, а также красивый малиновый цвет осенней листвы. Я стремился включить одного человека, который выделялся, прогуливаясь по тропинке, листвой падения на переднем плане и линией деревьев в качестве центральной точки фокусировки в моем кадре. Для этого я поместил эти аспекты в центр моего воображаемого прямоугольника, зная, что он содержит несколько ключевых точек фокусировки, связанных с отношением, и включил туман в сцену вдоль широкой дуги спирали.
Как вы можете видеть, спираль в основном имеет способ естественного продвижения вашего глаза от фокуса наружу. Вы можете увидеть еще несколько примеров спирали Фибоначчи, следуя этим удивительным фотографам природы в Instagram. .
Лучшие приложения для золотого сечения
Правильное приложение камеры может сделать вас лучшим фотографом. , но не каждое приложение камеры поддерживает Phi Grid или спираль Фибоначчи.
Если вы пользуетесь телефоном Android, то получите Camera Zoom FX (3 доллара). Это одно из 10 приложений, которые каждый должен установить в первую очередь на Android. , и не зря. Он поддерживает как сетку Фи, так и спираль Фибоначчи в качестве оверлеев. Просто выберите нужную сетку, составьте изображение и снимайте.
Если у вас iPhone, то Camera Awesome [больше не доступен] имеет спираль Фибоначчи, чтобы делать больше потрясающих фотографий. . Чтобы использовать Phi Grid, вам понадобится платное приложение, такое как Phi Camera [Больше не доступно].
Золотое сечение против правила третей
В Интернете много споров о том, что лучше: золотое сечение или правило третей. Видео выше дает некоторое представление о двух стилях, но мы хотим услышать от вас: какая техника композиции лучше и почему?
Имя Бога и число Бога (золотое сечение). Как связаны ряд Фибоначчи с именем Всевышнего в арийских Ведах и иудейской Торе. Наш РОД или их ЯХВЕ.
Кирилица и имя Всевышнего.
Написать эту статью меня сподвигло случайное видео одного хупцеватого израильского еврея Ишаягу Рубинштейна, который пытается убедить весь мир, что иудеи поклоняются правильному господу, тоесть их Сатан (Син) и есть Бог. В очередной раз иудеи с таким нахальством натягивают свою сатанинскую идеологию на глобус, что аж Тора трещит по швам. Но некоторые доверчивые люди на это ведуться. Поэтому не могу пройти мимо, и считаю своим долгом пролить свет наследия предков на происхождение имени Бога. А так же расскажу вам, почему иудеи утверждают, что имя бога ими зашифровано (ЯХВЕ – это шифр, тетраграмма) и его нельзя произносить вслух.
Итак, начну с главного. Имя Бога содержит в своём словесном шифре код Золотой пропорции и соответственно число Фибоначчи (открытие 13 века), которое древние называли «золотым сечением». Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в космосе, природе, науке, искусстве – во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему никогда не изменяло.
Золотое сечение известно было далеко до рождения учёного Леонардо Фибоначчи, но как известно всё новое – это хорошо забытое старое. Пирамида Хеопса, например, построена с применением расчётов, основанных на золотом сечении. А её возраст около 10 тыс.лет. Строители средневековых готических церквей и соборов Руси и Европы также возводили эти величественные сооружения в соответствии с золотой пропорцией. Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.
Как сказал великий Пифагор: числа правят миром. Русские жрецы знали это задолго до Пифагора, поэтому и написали Каббалу, ну и разумеется основы знаний поместили в Ведах (например фундаментальные основы квантовой физики, которые нашли своё подтверждение только в конце 20 века. О этом расскажу позже.
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.
Прекрасным примером служит афинский Парфенон, изумительный фронтон которого идеально вписывается в золотой прямоугольник. Образцом того, как использовал золотой прямоугольник в своих творениях Леонардо да Винчи, может послужить его знаменитый рисунок «Витрувианский человек», а также лицо Моны Лизы, прекрасно вписывающееся в такой прямоугольник. Подобные пропорции использованы в композиции «Тайной вечери».
Число Фибоначчи (число Бога, золотое сечение): 62% / 38% = 1,61…
Код Золотого Сечения состоит из чисел 10, 5, 6, 5. Не путать с Рядом Фибоначчи.
Ряд Фибоначчи: 0, 1, 1, 2, 3, 5, 8… и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
Распятие Исуса – крест, хоть и на первый взгляд не ведический тоже содержит число Фибоначчи: 16/10 = 1,6. Видео на эту тему прилагаю.
Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть. Все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения, даже закручивание по спирали — «кривой жизни». Учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике.
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Мы считаем человека красивым и здоровым, если пропорции его тела и лица соответствуют золотому сечению. Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
Так же прилагаю видео на тему о Золотом Сечении, которое признанно учёными главным числом во Вселенной.
Древние видели в золотом сечении отражение космического порядка, поскольку во вселенной так же всё подчинено золотому сечению, поэтому его называют числом Бога.
Код Золотого Сечения состоит из чисел 10, 5, 6, 5, так как 105/65 = 1,61.
Иудеи украли и присвоили себе как русскую Каббалу, так и шумерские, египетские религиозные тексты, на базе которых они написали Тору, намешав туда африканского откровенного сатанизма. Прочтя религиозные тексты белой расы евреи познакомились с числом Бога, а так же с кодировкой его имени в арийской традиции, которую решили применить в Торе при переводе с арамейского и на иврит. А принцип прост — 10, 5, 6, 5 – это номера букв алфавита. Иудеи применили свой алфавит и у них получилось слово «ЯХВЕ», смысл которого они объяснить не способны. Потому, что принцип-то украден у белой расы, которая разговаривала на русском. И арамейский язык и все языки мира – это производные от русского, что доказано Платоном Лукашевичем.
Итак, в шумерских текстах, в египетской книге Мертвых, в аийских Ведах речь шла конечно же не о сатане, а о Всевышнем. Иудеи же по принципу кодировки имени Бога, закодировали имя Сатана (Сина), назвав его Яхве. Однако эта примитивная кодировка не несёт смысловой нагрузки, поскольку куцый еврейский язык состоит из 22 букв алфавита, он примитивен как мозг еврея. А вот могучий русский язык, состоящий из 49 букв алфавита, который по преданию был дан самим Богом белой расе потрясающим образом раскрывает кодировку Золотого Сечения. Причем, у Бога есть чувство юмора. Даже кастированная Кириллом и Мефодием буковица сохранила силу Бога.
Итак, имя бога закодировано как последовательность букв в древнем алфавите пронумерованных числами 10, 5, 6, 5.
Согласно древнеславянской буковице:
10-я буква буковицы – буква З (земля) соответсвует цифре 7;
5-я буква буковицы – буква Д (добро), соответсвует цифре 4;
6-я буква буковицы – буква Е (есть) соответсвует цифре 5.
Ведическая математика – это взрыв еврейского мозга.
Добро – пятая буква в славянском алфавите, которая является символом чистоты и добра. Истинное значение этого слова «добро, добродетель», а так же «развитие», «накопление божественного», «полнота гармонии», «созданность находящаяся над чем-то». При этом в букву Добро Веды вкладывают не только чисто человеческие черты характера, но и добродетель, которой должны придерживаться все люди, любящие Отца небесного. Под Добром, прежде всего, усматривают добродетель с точки зрения поддержания человеком ведических нравсвенных норм, которые символизируют Заповеди Бога.
Числовое значение буквы Добро обозначается цифрой 4, т.е. четверкой. Что же вкладывали славяне в это число? Прежде всего, четверка символизировала четыре стихии: огонь, вода, земля и воздух, четыре конца священного креста – Свастики (Галактика Млечный путь, закручивается по спирали как последовательность Фибонначи), четыре стороны света и четыре угла в комнате. Таким образом, четверка была символом устойчивости и даже незыблемости.
Есть – шестая буква славянской буковицы. Это одно из самых многогранных слов старославянской азбуки. Это слово обозначается такими словами, как «бытие», «проявленная форма бытия», «космическая форма жизни», 5 элементов жизни, а так же «достаток», «присутствие бога», «естество», «природа» и другие синонимы, которые выражают значение этих слов.
У древних славян пятерка была символом – победной войны и оправданного риска ради спасения своего рода. Ярким свидетельством этому служит проведение битв славянами преимущественно по пятницам. Пятница у славян была символом числа пять. Славяне предпочитали проводить битвы и сражения по пятницам исключительно потому, что считали пятерку счастливым числом и благодаря этому надеялись выиграть сражение.
В христианском Священном Писании пятерка так же является символом благодати и милости. Масло для священного помазания состояло из 5 частей, в которые входили 5 ингредиентов, а при осуществлении обряда «окуривания» также используется 5 различных ингредиентов, таких как: ладан, стакт, оних, ливан и халван. А вы не верили, что христианство тайно основано на Ведах? Идём далее.
Земля – десятаятая буква древнеславянской буковицы, значение которой представляется как «земля» или «страна». Эта буква-слово Земля употреблялась в таких значениях, как «край», «страна», «народ», «земля», «РОД», «род человеческий», «обитель детей бога» или же под этим словом понималось тело человека. Многозначность этого слова раскрывается только в русском языке. Все мы живем на земле, в своей стране, и относимся к какой-либо народности. Поэтому слово-буква Земля представляет собой понятие, за которым скрывается общность народа. Причем все начинается с малого, а заканчивается чем-то большим и необъятным. То есть в этой букве Бог воплотил следующее явление: каждый человек является частью семьи, каждая семья относится к общине, а каждая община в совокупности представляет собой народ, который живет на определенной территории, называемой родным краем. И вот эти лоскуты земли, которые мы называем родным краем, объединены в огромную страну, где есть единый Бог. Однако кроме глубоко философского смысла в букве Земля скрывается число, которое непосредственно связано с жизнью. Это число 7 – семь, семерка, седмица. Что может знать современная молодежь о цифре 7? Только лишь то, что семерка приносит удачу. Однако для древних славян семерка была очень значимым числом. Число семь для славян обозначало число духовного совершенства, на которое легла Божья печать.
Когда в буковице убрали буквы Есмь и Зело, десятой буквой славянского алфавита стала буква Ижен.
Ижен – буква, смысл которой «вселенная», «система миропорядка», «истина вселенского масштаба», «уравновешивать, гармонизировать», равновесие и гармония в природе», а так же «наше, своё, родное», «то, что было известно нашим предкам», «то, что нерушимо существовало и существует при нас». Бытовое значение можно выразить словами «ежели», «если» и «когда». Смысл этих слов по сей день не изменился, просто в повседневной жизни современные славяне используют синонимы Ижен: если и когда. Интересна числовая расшифровка этой буквы. Ведь Ижен соответствует цифра 10 – десять, десятка, декада, как мы сегодня называем это число. У славян число десять считается третьим числом, которое обозначает божественное совершенство и упорядоченную завершенность. Если вы обратитесь к истории и различным источникам, то увидите, что десятка имеет глубокий религиозно-философский смысл:
· 10 заповедей – это завершенный Божий кодекс, который открывает нам основные правила благодетели в христианстве;
· 10 поколений представляют полный цикл семьи или нации;
· в молитве «Отче наш!» содержится 10 моментов, которые представляют собой завершенный цикл принятие Бога, почтение Всевышнего, мольба об избавлении и логически завершающим моментом является признание Его вечности.
И это лишь неполный цикл упоминаний числа 10 в различных источниках. Таким образом Кирилл и Мефодий упростили буковицу с особым религиозным смыслом, чтобы сохранялся код имени Бога – золотое сечение и обосновать христианство ведическим законом и языком Бога – русской буковицей.
Теперь расшифровка имени Бога по древнеславянски по ведическому закону Первозаконию при 49 буквах алфавита: 10, 5, 6, 5 – Земля (Род, община) Добро (развитие, гармония) Есть Добродетель (накопление божественного) – тоесть бог РОД. РОД – это и есть народ на земле, общиной живущий по божьему закону. Поэтому мы – дети Бога, а не его рабы, в отличие от евреев, которые рабы своему Яхве согласно их Торы.
10, 5, 6, 5 – РОДа развитие и гармония есть накопление бога, что добродетельно. Такова словесная формула божественного золотого сечения для славян. Поэтому иудеи пытаются её разрушить физически уничтожая род белой расы. Видите как глубоко заложена иудейская ненависть к славянам – они посягают на золотое сечение самого Всевышнего, на детей бога – на богоизбранный народ. Воры и мошенники украли священные арийские тексты, приписали себе богоизбранность и уничтожают истинных носителей божественного провидения. Вы не в одном языке мира не найдёте такого глубокого смыслового толкования кода Бога, только в русском. Иврит и идиш просто отдыхают. Поэтому иудеи и не могут объяснить смысл своей тетраграммы Яхве – этого смысла просто не существует, кроме как сокрыть факт воровства кода золотого сечения у арийских народов, у белой расы, которую они так ненавидят.
Алфавит после христианской реформы:
10-я буква буковицы – буква І (ижен) соответсвует цифре 10;
5-я буква буковицы – буква Д (добро), соответсвует цифре 4;
6-я буква буковицы – буква Е (есть) соответсвует цифре 5.
Расшифровка имени Бога в христианской традиции (после реформы Кирилла и Мефодия) выглядит следующим образом: Ижен (вселенская истина, система миропорядка) Добро Есть Добродетель.Или попростолюдински:Когда Добро есть добродетель.Иначе говоря,Истинной системой миропорядка (своё родное,что нерушимо существовало и существует при нас)есть накопление божественной гармонии и развитии рода человеческого.Что тоже Ведам не противоречит. Христианская словесная кодировка Золотого Сечения по смыслу соответствует Ведам, но никак не Торе с ритуальными убийствами и ростовщичеством, которые потому и названы сатанизмом, поскольку разрушают божественную гармонию на планете.
Любопытно так же расшифровка имени пророка Исуса.
И – истина на вселенском уровне, наше, своё, родное, «то, что было известно нашим предкам»;
С – слово, мысль произнесённая, поток энергии;
У – зов-послание, нахождение рядом.
Получаем: Исус – это Свой, родной, тот, кого знали наши предки, кто находится рядом проявляя себя потоком энергии в посланиях, произнесенных словами.Мощная словесная формула. Сын РОДа, пришедший защитить белую расу от иудеев проповедуя иудеям Веды – высший нравственный закон, отвращая их от сатанизма, запрещая ростовщичество и ритуальные убийства. В Ведах Исус упоминается как человек-пророк белой расы из рода Трёхлунных.
В примитивном иудаизме вы такого глубокого толкования не найдёте. Очевидно, что имя Исус придумали жрецы белой расы основываясь на русской буковице. Христианство пошло из Руси в Европу для обуздания иудаизма.
В Евангелиях есть фраза Исуса к апостолам: В Самару не ходите, там греха нет. Самара – исконно русский город, созданный волхвами. Аналогичное название города есть и во Франции (Галии), где проповедовал Исус иудеям. Европа была частью Русской Империи. Примечательно, в иудейской Торе Самара упоминается как город греха (раввины сфальсифицировали шумерские тексты). Что для славян хорошо, то для евреев – плохо. Что для детей Бога хорошо, то для сатанистов (рабов их господа) – плохо. И наоборот. Потому и изгоняли иудеев отовсюду, бегали сатанисты как зайцы с чемоданами по всему Евразийскому континенту.
Славянская буковица из 49 букв ( квадрат 7 умножить на 7) – это кладезь божественной мудрости, поэтому иудеи и жидовствующие попы её уничтожали путём реформ – сократили до 33 букв. В ней заложены готовые к восприятию смысловые словесные конструкции по вертикали, по горизонтали и по диагонали. Например, Боги Ведами глаголят Добро есть Истина. Видео прилагаю. Ведайте русы наследие предков своих, ибо это божественная истина, которая полностью подтверждается наукой,о чём ещё расскажу…
ПОСТСКРИПТУМ: в древней славянской традиции тетраграмма имени Бога звучит как ИДЕД, что трансформировалось в привычное для нас слово «идёт» (смягчение гласного звука и оглушение последней согласной буквы при произношении). Тоесть, БОГ — это тот, кто идёт. А теперь вспомните постулат, который признают абсолютно все, даже атеисты, воинствующие материалисты: ДВИЖЕНИЕ — ЭТО ЖИЗНЬ! Тоесть, Бог — тот, кто дает жизнь. Все эти смыслы пришли из Вед и божественного могучего русского языка. Вот почему, у славян принято почитать и поминать Дедов — это мир Бога, где живут души наших предков.
Татьяна Мельничук | Числа Фибоначчи
Числа Фибоначчи — код природы
Леонардо Фибоначчи (1170-1250 г.г.)
Фибоначчи (Леонардо из Пизы) — итальянский математик. Он стал первым великим математиком средневековой Европы. Рожденный в Пизе в богатой купеческой семье Фибоначчи пришел в математику благодаря практической потребности установления деловых контактов. В молодости Леонардо много путешествовал, сопровождая своего отца в деловых поездках. До нас дошли сведения о его длительном пребывании в Византии и на Сицилии. Во время таких поездок он много общался с местными учеными. От арабских математиков Леонардо узнал о системе цифр, придуманной в Индии и уже принятой на тот момент в арабском мире. В одном из своих трудов «Книга вычислений» Фибоначчи описал индо-арабскую систему счисления и преимущества ее использования по сравнению с римской.
Невозможно представить современную математику без использования десятичной системы счисления и арабских цифр, начало использования которых в Европе было положено именно Фибоначчи. Являясь пизанским банкиром, торговавшим в Тунисе и занимавшимся там ссудами и откупом налогов и таможенных сборов, Леонардо Фибоначчи применил к банкирскому счетоводству арабские цифры, ознакомив, таким образом, с ними Европу.
Числовая последовательность, которая названа в его честь, была открыта в ходе решения задачи о кроликах, излагаемой Фибоначчи в своей книге «Liber abacci» (1202 год, рукопись книги сохранилась до наших дней):
Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?
Несложно убедиться, что число пар в каждый из двенадцати последующих месяцев будет равно:
Иными словами, число пар кроликов представляет собой последовательность, каждый член которой равен сумме двух предыдущих. Эта последовательность известна как ряд Фибоначчи, а числа, образующие её, называют числами Фибоначчи. Оказывается, эта последовательность имеет множество интересных с точки зрения математики свойств. Например, можно разделить линию на два сегмента так, что соотношение между большим и меньшим сегментом будет пропорционально соотношению между всей линией и большим сегментом. Этот коэффицент пропорциональности, приблизительно равный , известен как золотое сечение. В эпоху Возрождения заметили, что именно эта пропорция, соблюденная в архитектурных сооружениях, является наиболее гармоничной с эстетической точки зрения. Число также называют числом Фи.
Последовательность Фибоначчи повсеместно встречается в природе. Например, закономерности этой последовательности сопровождают рост раковины моллюска, шишки хвойного дерева, листьев и ветвей растений, цветка подсолнуха, тела ящерицы, появление морских волн, строение головного мозга и других органов человека, строение галактик, пирамид в Гизе и Мексике.
Наглядное представление о числах Фибоначчи я предлагаю почерпнуть из короткого иллюстративного видеоролика:
Вернуться назад…
что такое золотое сечение простыми словами. Тайны мироздания в числах. Ряд Фибоначчи и золотое сечение
Числа Фибоначчи… в природе и жизниЛеонардо Фибоначчи – один из величайших математиков Средневековья. В одном и своих трудов “Книга вычислений” Фибоначчи описал индо-арабскую систему исчисления и преимущества ее использования перед римской.
Определение
Числа Фибоначчи или Последовательность Фибоначчи – числовая последовательность, обладающая рядом свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.), что подтверждает существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений.
Последовательность Фибоначчи начинается так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
2.
Полное определение чисел Фибоначчи
3.
Свойства последовательности Фибоначчи
4.
1. Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера. Отношение же каждого числе к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют(ФИ).
2. При делении каждого числа на следующее за ним, через одно получается число 0.382; наоборот – соответственно 2.618.
3. Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236.
5.
Связь последовательности Фибоначчи и «золотого сечения»
6.
Последовательность Фибоначчм асимптотически (пpиближаясь все медленнее и медленнее) стpемится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи pазделить на пpедшествующий ему (напpимеp, 13:8), pезультатом будет величина, колеблющаяся около иppационального значения 1.61803398875… и чеpез pаз то пpевосходящая, то не достигающая его. Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Особые названия этому соотношению начали давать еще до того, как Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи
Представим золотое сечение на примере отрезка.
Рассмотрим отрезок с концами A и B. Пусть точка С делит отрезок AB так что,
AC/CB = CB/AB или
AB/CB = CB/AC.
Представить это можно примерно так: A-–C—–B
7.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
8.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью 0,618…, если AB принять за единицу, AC = 0,382.. Kак мы уже знаем числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи.
9.
Пропорции Фибоначчи и золотого сечения в природе и истории
10.
Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи. Просто удивительно, сколько постоянных можно вычислить пpи помощи последовательности Фибоначчи, и как ее члены проявляются в огромном количестве сочетаний. Однако не будет преувеличением сказать, что это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых.
11.
Пpиводимые ниже примеры показывают некоторые интересные приложения этой математической последовательности.
12.
1. Pаковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Форма спирально завитой раковины привлекла внимание Архимеда. Дело в том, что отношение измерений завитков раковины постоянно и равно 1.618. Архимед изучал спираль раковин и вывел уравнение спирали. Cпираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.
2. Растения и животные. Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Cпираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Cовместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Cпиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль «кривой жизни».
Cреди придорожных трав растет ничем не примечательное растение — цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Ящерица живородящая. В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.
И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
Пьер Kюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
3. Космос. Из истории астрономии известно, что И. Тициус, немецкий астроном XVIII в., с помощью этого ряда (Фибоначчи) нашел закономерность и порядок в расстояниях между планетами солнечной системы
Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Cосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти Тициуса в начале XIX в.
Pяд Фибоначчи используют широко: с его помощью представляют архитектонику и живых существ, и рукотворных сооружений, и строение Галактик. Эти факты – свидетельства независимости числового ряда от условий его проявления, что является одним из признаков его универсальности.
4. Пирамиды. Многие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скоpее неразрешимая головоломка из числовых комбинаций. Замечательные изобpетательность, мастерство, время и труд аpхитектоpов пирамиды, использованные ими пpи возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической и символы были единственным средством записи открытий. Kлюч к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.
Площадь тpеугольника
356 x 440 / 2 = 78320
Площадь квадpата
280 x 280 = 78400
Длина ребра основания пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды -484.4 фута (147.6 м). Длина ребра основания, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) – это числа из последовательности Фибоначчи. Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618. Некоторые современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью – передать знания, которые они хотели сохранить для грядущих поколений. Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль.
Пирамиды в Мексике. Hе только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения, то же самое явление обнаpужено и у мексиканских пиpамид. Возникает мысль, что как египетские, так и мексиканские пиpамиды были возведены пpиблизительно в одно вpемя людьми общего происхождения.
Последовательность Фибоначчи, ставшая известной большинству благодаря фильму и книге «Код да Винчи», это ряд чисел, выведенный итальянским математиком Пизанским Леонардо, более известным под псевдонимом Фибоначчи, в тринадцатом веке. Последователи ученого заметили, что формула, которой подчинен данный ряд цифр, находит свое отображение в окружающем нас мире и перекликается с другими математическими открытиями, тем самым открывая для нас дверь в тайны мироздания. В этой статье мы расскажем, что такое последовательность Фибоначчи, рассмотрим примеры отображения этой закономерности в природе, а также сравним с другими математическими теориями.
Формулировка и определение понятия
Ряд Фибоначчи — это математическая последовательность, каждый элемент которой равен сумме двух предыдущих. Обозначим некой член последовательности как х n. Таким образом, получим формулу, справедливую для всего ряда: х n+2 =х n +х n+1. При этом порядок последовательности будет выглядеть так: 1, 1, 2, 3, 5, 8, 13, 21, 34. Следующим числом будет 55, так как сумма 21 и 34 равна 55. И так далее по такому же принципу.
Примеры в окружающей среде
Если мы посмотрим на растение, в частности, на крону из листьев, то заметим, что они распускаются по спирали. Между соседними листьями образуются углы, которые, в свою очередь, образуют правильную математическую последовательность Фибоначчи. Благодаря этой особенности каждый отдельно взятый листочек, который растет на дереве, получает максимальное количество солнечного света и тепла.
Математическая загадка Фибоначчи
Известный математик представил свою теорию в виде загадки. Звучит она следующим образом. Можно поместить пару кроликов в замкнутое пространство для того, чтобы узнать, какое количество пар кроликов родится в течении одного года. Учитывая природу этих животных, то, что каждый месяц пара способна производить на свет новую пару, а готовность к размножению у них появляется по достижении двух месяцев, в итоге он получил свой знаменитый ряд чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 — где показано количество новых пар кроликов в каждом месяце.
Последовательность Фибоначчи и пропорциональное соотношение
Этот ряд имеет несколько математических нюансов, которые обязательно нужно рассмотреть. Он, приближаясь медленнее и медленнее (асимптотически), стремится к некоему пропорциональному соотношению. Но оно иррациональное. Другими словами, представляет собой число с непредсказуемой и бесконечной последовательностью десятичных чисел в дробной части. Например, соотношение любого элемента ряда варьируется около цифры 1,618, то превосходя, то достигая его. Следующее по аналогии приближается к 0,618. Что есть обратно пропорциональным к числу 1,618. Если мы поделим элементы через один, то получим 2,618 и 0,382. Как вы уже поняли, они также являются обратно пропорциональными. Полученные числа называются коэффициентами Фибоначчи. А теперь объясним, для чего мы выполняли эти вычисления.
Золотое сечение
Все окружающие нас предметы мы различаем по определенным критериям. Один из них — форма. Какие-то нас привлекают больше, какие-то меньше, а некоторые и вовсе не нравятся. Замечено, что симметричный и пропорциональный объект гораздо легче воспринимается человеком и вызывает чувство гармонии и красоты. Цельный образ всегда включает в себя части различного размера, которые находятся в определенном соотношении друг с другом. Отсюда вытекает ответ на вопрос о том, что называют Золотым сечением. Данное понятие означает совершенство соотношений целого и частей в природе, науке, искусстве и т. д. С математической точки зрения рассмотрим следующий пример. Возьмем отрезок любой длины и разделим его на две части таким образом, чтобы меньшая часть относилась к большей как сумма (длина всего отрезка) к большей. Итак, примем отрезок с за величину один. Его часть а будет равна 0,618, вторая часть b , выходит, равна 0,382. Таким образом, мы соблюдаем условие Золотого сечения. Отношение отрезка c к a равняется 1,618. А отношение частей c и b — 2,618. Получаем уже известные нам коэффициенты Фибоначчи. По такому же принципу строятся золотой треугольник, золотой прямоугольник и золотой кубоид. Стоит также отметить, что пропорциональное соотношение частей тела человека близко к Золотому сечению.
Последовательность Фибоначчи — основа всего?
Попробуем объединить теорию Золотого сечения и известного ряда итальянского математика. Начнем с двух квадратов первого размера. Затем сверху добавим еще квадрат второго размера. Подрисуем рядом такую же фигуру с длиной стороны, равной сумме двух предыдущих сторон. Аналогичным образом рисуем квадрат пятого размера. И так можно продолжать до бесконечности, пока не надоест. Главное, чтобы величина стороны каждого последующего квадрата равнялась сумме величин сторон двух предыдущих. Получаем серию многоугольников, длина сторон которых является числами Фибоначчи. Эти фигуры называются прямоугольниками Фибоначчи. Проведем плавную линию через углы наших многоугольников и получим… спираль Архимеда! Увеличение шага данной фигуры, как известно, всегда равномерно. Если включить фантазию, то полученный рисунок можно проассоциировать с раковиной моллюска. Отсюда можем сделать вывод, что последовательность Фибоначи — это основа пропорциональных, гармоничных соотношений элементов в окружающем мире.
Математическая последовательность и мироздание
Если присмотреться, то спираль Архимеда (где-то явно, а где-то завуалированно) и, следовательно, принцип Фибоначчи прослеживаются во многих привычных природных элементах, окружающих человека. Например, все та же раковина моллюска, соцветия обычной брокколи, цветок подсолнечника, шишка хвойного растения и тому подобное. Если заглянем подальше, то увидим последовательность Фибоначчи в бесконечных галактиках. Даже человек, вдохновляясь от природы и перенимая ее формы, создает предметы, в которых прослеживается вышеупомянутый ряд. Тут самое время вспомнить и о Золотом сечении. Наряду с закономерностью Фибоначчи прослеживаются принципы данной теории. Существует версия, что последовательность Фибоначчи — это своего рода проба природы адаптироваться к более совершенной и фундаментальной логарифмической последовательности Золотого сечения, которая практически идентична, но не имеет своего начала и бесконечна. Закономерность природы такова, что она должна иметь свою точку отсчета, от чего отталкиваться для создания чего-то нового. Отношение первых элементов ряда Фибоначчи далеки от принципов Золотого сечения. Однако чем дальше мы его продолжаем, тем больше это несоответствие сглаживается. Для определения последовательности необходимо знать три его элемента, которые идут друг за другом. Для Золотой последовательности же достаточно и двух. Так как она является одновременно арифметической и геометрической прогрессией.
Заключение
Все-таки, исходя из вышесказанного, можно задать вполне логичные вопросы: «Откуда появились эти числа? Кто этот автор устройства всего мира, попытавшийся сделать его идеальным? Было ли всегда все так, как он хотел? Если да, то почему возник сбой? Что будет дальше?» Находя ответ на один вопрос, получаешь следующий. Разгадал его — появляются еще два. Решив их, получаешь еще три. Разобравшись с ними, получишь пять нерешенных. Затем восемь, далее тринадцать, двадцать один, тридцать четыре, пятьдесят пять…
Леона́рдо Пиза́нский (лат. Leonardus Pisanus, итал. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи.
Подробнее тут:http://ru.wikipedia.org/wiki/%D4%E8%E1%EE%ED%E0%F7%F7%E8
Последовательность Фибоначчи, известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:
Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.
Последовательность Фибоначчи и Кролики
В итоге получается такой ряд цифр: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Его можно продолжать бесконечно долго. Его суть в том, что каждое следующее число является суммой двух предыдущих.
У этого ряда есть несколько математических особенностей, которых обязательно нужно коснуться. Он асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Так отношение какого-либо члена ряда к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.
К чему всё это?
Так мы приближаемся к одному из самых загадочных явлений природы. Смекалистый Леонардо по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.
Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.
Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.
Золотое Сечение — Отрезок
Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 1,618, а с к b 2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.
Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.
Золотое сечение и Человеческое тело
Изображение: marcus-frings.de
Последовательность Фибоначчи — Анимация
Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.
Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.
Спираль Фибоначчи
Ничего не напоминает?
Фото: ethanhein on Flickr
И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.
Алое многолистный:
Фото: brewbooks on Flickr
Броколи романеско:
Фото: beart.org.uk
Подсолнечник:
Фото: esdrascalderan on Flickr
Сосновая шишка:
Фото: mandj98 on Flickr
И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.
Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама она далека от совершенства, как и всё в этом мире.
Есть предположение, что ряд Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любого ряда достаточно знать три его члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Каждый член золотой логарифмической последовательности является степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: … z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 … Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?
Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55…
Здравствуйте, дорогие читатели!
Золотое сечение — что это такое? Числа Фибоначчи — это ? В статье — ответы на эти вопросы кратно и понятно, простыми словами.
Эти вопросы вот уже несколько тысячелетий будоражат умы всё новых и новых поколений! Оказывается математика может быть не скучной, а захватывающей, интересной, завораживающей!
Другие полезные статьи:Числа Фибоначчи — это что?
Поразителен тот факт, что при делении каждого последующего числа числовой последовательности на предыдущее получается число, стремящееся к 1,618.
Обнаружил эту загадочную последовательность счастливчик математик средневековья Леонардо Пизанский (более известный под именем Фибоначчи) . До него Леонардо да Винчи обнаружил в строении тела человека, растений и животных удивительным образом повторяющуюся пропорцию Фи = 1,618 . Это число (1,61) ученые еще называют «Числом Бога».
До Леонардо да Винчи эта последовательность чисел была известна в Древней Индии и Древнем Египте . Египетские пирамиды построены с применением пропорции Фи = 1,618.
Но и это еще не все, оказывается законы природы Земли и Космоса каким-то необъяснимым образом подчиняются строгим математическим законам последовательности чисел Фидоначчи .
Например, и ракушка на Земле, и галактика в Космосе построены с применением чисел Фибоначчи. Абсолютное большинство цветов имеет 5, 8, 13 лепестков. В подсолнухе, на стеблях растений, в закрученных вихрях облаков, в водоворотах и даже в графиках изменения курсов валют на Форексе, всюду работают числа Фибоначчи.
Посмотрите простое и занимательное пояснение, что такое последовательность чисел Фибоначчи и Золотое сечение в этом КОРОТКОМ ВИДЕО (6 минут):Что такое Золотое сечение или Божественная пропорция?
Итак, что такое Золотое сечение или Золотая или Божественная пропорция? Фибоначчи также обнаружил, что последовательность, которая состоит из квадратов чисел Фибоначчи является еще большей загадкой. Попробуем графически изобразить в виде площади последовательность:
1², 2², 3², 5², 8²…
Если вписать спираль в графическое изображение последовательности квадратов чисел Фибоначчи, то мы получим Золотое сечение,
по правилам которого построено все во вселенной, включая растения, животных, спираль ДНК, человеческое тело, … Список этот можно продолжать до бесконечности.
Золотое сечение и Числа Фибоначчи в природе ВИДЕО
Предлагаю посмотреть короткий фильм (7 минут), в котором раскрываются некоторые загадки Золотого сечения. При размышлениях о законе чисел Фибоначчи, как о первостепенном законе, который управляет живой и неживой природой, появляется вопрос: Эта идеальная формула для макромира и микромира возникла сама или ее кто-то создал и удачно применил?Что ВЫ думаете по этому поводу? Давайте вместе подумаем над этой загадкой и быть может мы приблизимся к .
Очень надеюсь, что статья была полезной для Вас и Вы узнали, что это такое Золотое сечение *и Числа Фибоначчи ? До новых встреч на страницах блога, подписывайтесь на блог. Форма подписки — под статьей.
Всем желаю много новых идей и вдохновения для их реализации!
Эта гармония поражает своими масштабами…
Здравствуйте, друзья!
Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?
Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.
Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)
Что такое золотое сечение?
Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию ?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.
Но, кроме этого, золотое сечение — это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».
До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.
Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.
В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:
Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:
Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.
Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:
Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.
Ряд Фибоначчи и золотое сечение
Продолжаем творить и наблюдать за магией математики и золотого сечения. В средние века был такой товарищ — Фибоначчи (или Фибоначи, везде по-разному пишут). Любил математику и задачи, была у него и интересная задачка с размножением кроликов =) Но не в этом суть. Он открыл числовую последовательность, числа в ней так и зовутся «числа Фибоначчи».
Сама последовательность выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… и дальше до бесконечности.
Если словами, то последовательность Фибоначчи — это такая последовательность чисел, где каждое последующее число, равно сумме двух предыдущих.
Причем здесь золотое сечение? Сейчас увидите.
Спираль Фибоначчи
Чтобы увидеть и прочувствовать всю связь числового ряда Фибоначчи и золотого сечения, нужно снова взглянуть на формулы.
Иными словами, с 9-го члена последовательности Фибоначчи мы начинаем получать значения золотого сечения. И если визуализировать всю эту картину, то мы увидим, как последовательность Фибоначчи создает прямоугольники все ближе и ближе к золотому прямоугольнику. Вот такая вот связь.
Теперь поговорим о спирали Фибоначчи, ее еще называют «золотой спиралью».
Золотая спираль — логарифмическая спираль, коэффициент роста которой равен φ4, где φ — золотое сечение.
В общем и целом, с точки зрения математики, золотое сечение — идеальная пропорция. Но на этом ее чудеса только начинаются. Принципам золотого сечения подчинен почти весь мир, эту пропорцию создала сама природа. Даже эзотерики, и те, видят в ней числовую мощь. Но об этом точно не в этой статье будем говорить, поэтому, чтобы ничего не пропустить, можете подписаться на обновления сайта.
Золотое сечение в природе, человеке, искусстве
Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.
И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.
Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.
Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.
Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.
Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:
от плеч до макушки к размеру головы = 1:1.618
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
от пупка до коленок и от коленок до ступней = 1:1.618
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618
Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».
Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.
Золотое сечение в природе и ее явлениях
Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:
в завитках человеческого уха мы можем увидеть золотую спираль;
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
и в молекуле ДНК;
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.
Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.
Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:
Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.
По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.
Абсолютно во всем живом и не живом можно прочесть высшую красоту и гармонию.
Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет. Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил.
Золотое сечение в искусстве
Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.
Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.
Золотые котики Фибоначчи
Ну и, наконец, о котиках! Вы задумывались о том, почему все так любят котеек? Они же ведь заполонили Интернет! Котики везде и это чудесно =)
А все дело в том, что кошки — идеальны! Не верите? Сейчас докажу вам это математически!
Видите? Тайна раскрыта! Котейки идеальны с точки зрения математики, природы и Вселенной =)
* Я шучу, конечно. Нет, кошки, действительно, идеальны) Но математически их никто не измерял, наверное.
На этом, в общем-то, все, друзья! Мы увидимся в следующих статьях. Удачи вам!
P. S. Изображения взяты с сайта medium.com.
Дизайн аквариума видео
Дизайн аквариума своими руками с фото-видео примерами
ДИЗАЙН АКВАРИУМА – ПОРЯДОК В ХАОСЕ!
правила акваскейпа при построении дизайна аквариумной композиции:
золотое сечение, ряд Фибоначчи, фрактальность природы.
Многие постоянные читатели и форумчане ФанФишка.ру знают, что недавно я, наконец-то, запустил свой амановский травник.
Мотивацией для создания такой красотищи у себя дома, послужило желание доказать, что аквариум Амано «по зубам» всем и каждому, что это реально, что это не так уж сложно…
И что важно лишь жгучее желание, усердие, терпение, фанатизм, если хотите… Ну и конечно жажда познания, опыт, а главное, как говорит сен-сей Такаши Амано, идея!
В данный момент созданный травник «зреет», в нем будет произведена корректировка и работа над ошибками. На это уйдет 1-2 месяца и чтобы не тратить драгоценное время, я начинаю цикл статей, в которых поделюсь своим опытом, знаниями и эмоциями. Очень хочется верить, что мой запал и жгучее пламя любви к аквариумистике подхватят другие ребята, ведь это, по сути, конечная цель ФФ – привить любовь к миру аквариумных рыбок.
В тоже время, хочу сказать, что я не претендую на лавры сен-сея Амано. Как любой человек, я ошибаюсь, постоянно учусь и познаю мир аквариумистики. Совершенства в аквариумистике нет, как, собственно, и в жизни вообще. Важен опыт и мнение каждого, важна консолидация аквариумистов. И новичков, и профи. В общем, задавайте вопросы, критикуйте, советуйте!
Итак, на создание травника у меня ушло четыре месяца. За это время, я перелопатил столько информации!!! Столько побегал по магазинам!!!… К свадьбе, наверное, так не готовятся, как я к своему травнику))). И вы знаете, какая главная проблема, с которой я столкнулся? Отсутствие четкой, полноценной информации по созданию аквариума в стиле аля`Амано. Информация или разрозненная, или обрывистая, или чересчур заумная. Нет практикума, нет примеров, нет пошаговой инструкции. Давайте же вместе восполним это пробел!
В любом изобразительном искусстве (живопись, скульптура, архитектура) существует множество правил, которые используются для построения композиции. Дизайн аквариума – это тоже искусство! Художник творит кистью, скульптор гипсом… аквариумист растениями, грунтом, камнями и корягами! Множество правил и принципов построения композиции подробно изложить в одной статье невозможно. Поэтому предлагаю поговорить лишь о самых главных: «Золотом сечении», «Числах Фибоначчи» и «Фрактальности природы».
Все выше перечисленные правила я знал и ранее, как и многие из вас. Когда впервые знакомишься с этими правилами, создается ощущение, что ты близок к разгадке вопроса бытия и божественного начала. Чувствуешь, так сказать, что «потрогал Бога за мизинец»! Это и не удивительно, ведь все сущее (живое и не живое, видимое и не видимое) подчинено этим БОЖЕСТВЕННЫМ ПРАВИЛАМ.
В этой статье я постараюсь доступно рассказать о применении этих правил при построении аквариумной композиции. И, конечно, привести примеры. Но, прошу Вас не останавливаться только на моей статье! В интернете вы найдете множество будоражащих разум достойных фото, видео и текстовых материалов на эту тему!
Золотое сечение в аквариуме
Люди различают окружающие их предметы по форме. Интерес к форме любого предмета может быть продиктован жизненной необходимостью, а может быть вызван и красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Правило золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Золотое сечение – это гармоническая пропорция!
Я намеренно не включаю в статью все математические формулы и геометрические построения, чтобы максимально упростить материл. Тем не менее, совершенно обойтись без них невозможно. Попробуем уловить суть.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как самая большая часть относится к меньшей. Или, другими словами, меньший отрезок так относится к большему, как больший ко всему отрезку.
Золотое сечение (золотая «божественная» пропорция, деление в крайнем и среднем отношении) — соотношение двух величин, равное соотношению их суммы к большей из данных величин. Приблизительная величина золотого сечения равна 1,6180339887. В процентном округлённом значении — это деление величины на 62 % и 38 % соответственно.
Золотое сечение (пропорцию) — 1,618 называют божественным(ой), так как — это «мерило» всего сущего, от червячка до человека, от улитки до слона, от ДНК до структуры Вселенной! В сети можно найти множество увлекательных научно-популярных фильмов и передач на эту тему. Посмотрите, не пожалеете.
В нашей (аквариумной) статье приведу лишь один пример золотых пропорций в теле человека.
Золотые пропорции в лице и руке,
ниже в теле
Пишу и вспоминаю развлечение из детства. Однажды, я узнал, что размер стопы примерно равен 1/8 роста человека. Когда я это сказал в классе, все как оголтелые схватились за линейки и давай друг друга мерить! А ведь это — упрощенный пример золотой пропорции. Самое интересное, что по такому же принципу работают судмедэксперты, археологи и палеонтологи когда восстанавливают картину целого из частей и останков. Конечно, там все серьезнее, чем «1,8 стопы», но принцип тот же – «Золотая пропорция»!!!
Теперь немного истории. Человек, который хотя бы раз слышал о золотом сечении, связывает его с именем Леонардо да Винчи. Леонардо действительно внес огромный вклад в мир искусства и в познание Вселенских правил. Но, справедливости ради, стоит отметить, что о золотом сечении знали уже и в Древней Греции, и во времена фараонов.
Над этим вопросом трудились тысячи лучших умов! Стоит упомянуть имя немецкого профессора Цейзинга (1855г.), который проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д. Любопытно! Фундаментально! Потрясающе!
РЯД ИЛИ ЧИСЛА ФИБОНАЧЧИС историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи. Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке», в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 и т.д.
Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
ФРАКТАЛЬНОСТЬ ПРИРОДЫ И АКВАРИУМИСТИКА
Понятие фрактальности больше связано с геометрией и визуальным отображением золотого сечения и ряда Фибоначчи.
Фрактал (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия, то есть однородности в различных шкалах измерения (любая часть фрактала подобна всему множеству целиком).
Ну, а теперь «человеческим языком». Вокруг каждой клетки, каждой молекулы физических тел «бесконечный космос» других клеточек и молекул. И во всем полная гармония — гармония фрактальной геометрии.
Фракталами называют бесконечно самоподобные фигуры, каждый фрагмент которых повторяется при уменьшении масштаба. Термин фрактал означает наличие тонкой, повторяющийся структуры, как в макро, так и в микро масштабе объекта.
Фрактальность проявляется во всем! В галактиках и клетках, в строении каждого кустика и дерева, снежинке и облачке. Даже молния фрактальна. Что уж говорить об изгибе береговой линий моря, озер, гор, полей и т.д… В конце концов, ритм биения нашего сердца (кардиограмма) – это тоже фрактал!
Все в пространстве фрактально! И угадайте «кто всему виной»? Конечно же Фибоначчи и его ряд 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…. ))) Куда ни кинь взгляд в природе, везде просматривается числовой ряд, где каждое последующее число является суммой двух предыдущих.
Можете понаблюдать, как прорастает из земли любое растение, и Вы с удивлением обнаружите, что сначала появляется один листик, потом два, чуть позже – три, затем пять… восемь… тринадцать. И никогда по-другому!
Вот элементарное визуальное отображение фрактальности
Вот фрактал в брокколи
А вот в дереве
Приведу еще пример, возьмем отдельно взятое деревце,
исходя из его единичной фрактальной структуры, можно определить, сколько и какие деревья будут в лесу, где оно стоит.
То же самое и в аквариумистике, – кустик, к кустику, камешек камешку. Одним словом, должна быть гармония! В аквариуме не должно быть разных по цвету и фактуре камней, не должно быть разных коряг. Сами элементы декора не должны быть одинаковыми по размеру, они должны быть установлены в нужном месте, а не абы как!
Для лучшего понимания и визуализации, ниже предлагаю посмотреть небольшие видео ролики о золотом сечении, ряде Фибоначчи и фрактале
Также рекомендую посмотреть х/ф «Фракталы: порядок в хаосе» (2008г.), фильм можно найти в поиске Яндекс или Google.
Из всего вышесказанного можно сделать вывод, что все в мире подчинено вышеописанным «божественным правилам». Дизайн аквариума – это искусственное воссоздание уголка живой природы. Отсюда можно сделать вывод: «Для того чтобы искусственное было максимально приближено к божественному, нужно при оформлении аквариума использовать указанные незыблемые правила!».
НА ЭТОМ ПЕРЕЛАГАЮ ЗАКОНЧИТЬ ТЕОРЕТИЧЕСКУЮ ЧАСТЬ И ПЛАВНО ПЕРЕЙТИ К ПРАКТИКЕ ПРИМЕНЕНИЯ ПОЛУЧЕННЫХ ЗНАНИЙ В АКВАРИУМИСТИКЕ
Из всего вышесказанного можно сделать вывод, что все в мире подчинено вышеописанным «божественным правилам». Дизайн аквариума – это искусственное воссоздание уголка живой природы. Отсюда можно сделать вывод: «Для того чтобы искусственное было максимально приближено к божественному, нужно при оформлении аквариума использовать указанные незыблемые правила!».
Возьмите любое произведение искусства.
Например, картину И.И. Шишкина «Утро в сосновом лесу»!
Автор неукоснительно следовал принципам золотого сечения. Главный объект находится в сильной точке, а все объекты расположены в золотых треугольниках.Аквариум – та же картина, а это значит, что его дизайн напрямую зависит от тех же правил, что и в изобразительном искусстве
Давайте же рассмотрим, как найти золотое сечение и сильные точки в аквариуме. Ведь это очень важно — решить где, в каком месте композиции должен быть расположен ее центр.
Итак, вернемся к числам Фибоначчи 1,1,2,3,5,8,13…
Для начала делим видовое стекло аквариума на 3, 5 или 8 равных частей по горизонтали и по вертикали.
Примечание: Мой скейп был выполнен в аквариуме с панорамным стеклом. Процесс нахождения сильных точек в таком случае усложняется. Я сфотографировал свой аквариум и по фото определял точки. Не забывайте, что все схемы и приемы относятся к той картинке, которую видит зритель, а не к геометрическим размерам банки. Речь идет, прежде всего, о проекции.
1:2 2:3 3:5
Я рекомендую использовать пропорцию 3 к 5. На 8 частей легче всего делить прямоугольник – 3 раза пополам. Для начала можно пользоваться рулеткой и маркером, потом появится навык размечать аквариум на глаз.
Затем выделяем оси, делящие целое на 3 и 5 равных частей.
И на пересечении осей получаем «сильную точку».
Всего таких точек может быть четыре. Но, у нас должен быть один центр! Выбираем любую из них, а про остальные забываем.
Ниже фото дизайна Такаши Амано, в которых автор умело располагает контрастный, выразительный центр в «сильной точке» аквариума
Вот еще один легкий способ провести золотое сечение в аквариуме.
Измерьте длину аквариума и разделите полученное значение на 2.61803.
Пример: Длина = 800мм / 2.61803 = 305.57322мм (округляем 305мм). Второй отрезок соответственно равен 800мм – 305мм = 495мм.
Делаем отметки, проводим линию. Такую же операцию проводим и с высотой аквариума.
Учтите, что высоту не нужно мерить «по самую крышку». Помните, должна быть картина – это то, что видит человек. После этого, вы можете провести другие линии пересечения – «золотые треугольники».
Ну, а дальше? А дальше… полет вашей фантазии, полет мысли о размещении вашей идеи в золотом сечении аквариума… Сначала мысленно, потом вертя в руках добытый декор (камни, коряги), при этом представляя их сочетание с растениями. И только потом — в самом аквариуме ))).
Итак, подведем итоги! Мы научились находить сильную точку в аквариумной композиции, а также проводить золотые линии и треугольники. Они помогут нам воплотить нашу идею в жизнь. Полученные знания позволят нам выстроить правильный, гармоничный дизайн в своем водоеме. Аквариум, который будет основан на вышеописанных принципах, будет естественным, природным, красивым и приятным для восприятия.
При построении аквариумной композиции существуют и другие, «менее значимые правила«: подбора растений, декораций, порядок расстановки камней, перспективы и объема аквариума…, но, по сути, все они так или иначе связаны с фундаментальными «божественными пропорциями» и рядом Фибоначчи.
Об этих, «менее значимых», но очень важных правилах я обязательно расскажу в следующих статьях.
fanfishka.ru>
Основы аквариумного дизайна
Акваскейп является давно изученным видом искусства, который позволяет создавать подводный пейзаж. Вдохновение для многих работ прибывает из подводных местоположений, также естественных пейзажей, таких как горы, джунгли, пустыни, водопады и многие другие. Прежде, чем создать красивый дизайн аквариума своими руками, вам понадобится функциональная составляющая аквариумной среды. Некоторые водные растения требуют, чтобы им подавалось насыщенное освещение и питательные вещества.
Низкие расходы на эксплуатацию акваскейпа позволяют расходовать невысокое количество углекислого газа, меньше удобрений и освещения. Рассеянное или тусклое освещение может быть столь же ошеломляющим, поскольку растения создадут красивые блики. Для аквариумного дизайна обычно используют растения, камни и деревянные коряги.
Виды акваскейпов
Стиль «Ивагуми» – это каменный дизайн аквариума, который пришел из Японии. Все элементы декора тонкие и заостренные, но поддерживаются плавными элементами. Крупные камни с неровной поверхностью помещены в центральную часть резервуара. Для создания аналогии с природной средой, камни имеют уклоны, о которые может ударяться вода.
Полюбуйтесь аквариумом в стиле «ивагуми».
Акваскейпы «ивагуми» часто используются для невысоких растений, которые высаживают на передний план. Акцент делается на скалах, а не на растениях. Темные и крутые камни пользуются спросом в данном виде дизайна.
Голландский стиль – это акваскейп из многих видов растений. В традиционном голландском стиле делается минимальный акцент на камнях и корягах. Выбор растений, их цвет и расположение являются ключевыми факторами для создания стиля. Голландские акваскейпы визуально выглядят как густые заросли подводных рек. Здесь часто можно увидеть ярко-красные, оранжевые, зеленые растения, которые высажены в больших количествах на переднем, центральном и заднем плане. Данный вид дизайна предполагает использование самых необычных и прихотливых форм растений. Чтобы подготовить акваскейп, понадобится много времени, умений и терпения.
Естественный стиль – воссоздает природные ландшафты. Растения, коряги и камни расположены таким образом, что напоминают озеро или реку из естественной среды. Этот стиль отличается хаотичностью форм, простотой. В нем используют исключительно природные материалы. Расположение растений, коряг и камней имеет ключевое значение. Рыбы – просто дополнение к красивому дизайну. Моделирование природной среды требует тщательного планирования. Растения для данного акваскейпа требуются невысокие, и крепятся к корягам, камням или высаживаются в грунт. Рыбки для него выбираются такие, которые смогут оживить ландшафт – барбусы, меченосцы, тетры, неоны, скалярии (стайные виды).
Симметрия
Чтобы сделать дизайн аквариума своими руками, нужно знать некоторые правила расстановки деталей.
- Избегайте симметрии – она придает акваскейпу слишком структурированный и опрятный вид. В природной среде не существует симметричных форм, а вы должны подражать окружающей среде. На природных скалах и растительности есть даже водорослевые наросты и немного грязи. Ассиметричные формы – ключ к созданию красивого дизайна.
- Основное внимание не должно быть сосредоточено на середине аквариума, но и немного от его центра. Используя золотое сечение (коэффициент, который уже давно был принят как математически эстетический) оптимальный координационный центр должен быть около 1: 1,62 длины аквариума.
- Вычисление «Золотого сечения»: измерьте длину аквариума с помощью сантиметра. Разделите длину на 100. Умножьте ваш ответ на 61.8 и запишите его. Теперь сделайте замеры одной стороны аквариума и сделайте небольшую отметку. Она должна быть координационным центром вашего акваскейпа.
- Что должно быть в центре? Центр должен быть самым большим, самым ярким или самым впечатляющим пунктом акваскейпа. Это может быть самая высокая скала, ярко-красное растение, крупная затопленная коряга или водопад в задней части аквариума.
Форма
- Избегите прямых линий и огражденных растений. Высокие саженцы на заднем плане, которые простираются, не рекомендуются. У природных видов часто есть очень немного прямых линий и мало непрерывности. Лучшие формы – те, которые имеют вид плавной кривой, или хаотичные.
- Естественные кривые и вогнутости будут плюсом – растения могут быть урезаны, чтобы создать по краям высоту, и понизить их в центральном плане, делая визуальное падение. Это поможет создать больше открытого пространства для плавания рыбок.
- Скошенные формы могут быть весьма привлекательны – треугольные формы и островки могут выглядеть натурально и эстетично. Скошенные тёмные растения выглядят подобно руслу реки, которое постепенно становится глубоким.
Посмотрите как можно оформить аквариум на 100 литров.
Передний, средний план и задний план (фон)
Важно различать каждый фон аквариума. У каждого фона должны присутствовать как высокие, так и низкие кусты растений. Средний план должен состоять из коряг, скал и растений средних размеров. У переднего плана должны быть красивые широколистные саженцы, такие как анубиас, криптокорина, стрелолист, апоногетон, и другие.
Можно сделать синтез – камни и коряги можно высадить и на передний план, а растения можно посадить на любом плане, чтобы улучшить внешний вид акваскейпа. Если вы можете себе позволить аквариум с открытым верхом, тогда у вас больше возможностей использовать камни и коряги, которые будут выпирать из водной глади.
Растения лучше высаживать так: начиная от переднего плана и заканчивая задним планом, визуально «спускаясь» вниз. Длинностебельные виды весят меньше, и легко запутываются в невысоких растениях, которые есть на переднем плане. Для установки скал, камней и их крепления друг к другу используйте силиконовый аквариумный клей. Он более безопасен, и позволяет держать мхи, папоротники и все провода на месте. Также мхи, папоротники и ползающие растения должны быть присоединены к твердой поверхности – дереву или камню. Сделайте это с помощью аквариумного клея или лёски.
AkvariumnyeRybki.ru>
Запуск и дизайн аквариума
Дизайн 300 литрового аквариума своими руками
Запуск и дизайн аквариума.
Создай настроение: ландшафтный дизайн аквариума
Ландшафтный дизайн аквариума. Как выращивать подводные шедевры? Вытворяшки
Аквариумный дизайн
Дизайн аквариума на 100 литров от Tropica
Дизайн аквариума на 180 литров от Tropica
Дизайн аквариума с африканскими цихлидами
Оформление аквариума на 120 литров для начинающих
Похожие статьи
Phi: Золотое сечение | Живая наука
Число фи, часто известное как золотое сечение, — математическое понятие, известное людям еще со времен древних греков. Это иррациональное число, такое как пи, и е, что означает, что его члены бесконечно идут после десятичной точки без повторения.
На протяжении веков вокруг фи было построено множество преданий, например, идея о том, что он олицетворяет совершенную красоту или уникально встречается в природе.Но многое из этого не имеет под собой реальных оснований.
Определение фи
Фи можно определить, взяв палку и разбив ее на две части. Если соотношение между этими двумя частями такое же, как соотношение между всей палкой и большим сегментом, считается, что эти части находятся в золотом сечении. Это было впервые описано греческим математиком Евклидом, хотя он назвал это «делением на крайнее и среднее отношение», согласно математику Джорджу Марковскому из Университета штата Мэн.2 = phi + 1
Это представление может быть преобразовано в квадратное уравнение с двумя решениями: (1 + √5) / 2 и (1 — √5) / 2. Первое решение дает положительное иррациональное число 1. 0.5 * 0,5 + 0,5
Это пять в половинной степени, умноженная на половину плюс половина.
Связанный: 11 самых красивых математических уравнений
Phi тесно связан с последовательностью Фибоначчи , в которой каждое последующее число в последовательности находится путем сложения двух предыдущих чисел. Эта последовательность идет 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Это также связано со многими заблуждениями.
Взяв отношение последовательных чисел Фибоначчи, вы можете приближаться к фи. Интересно, что если вы расширите последовательность Фибоначчи назад — то есть до нуля и на отрицательные числа — соотношение этих чисел будет приближать вас к отрицательному решению, маленький фи -0,6180339887…
Существует ли золотое сечение в природа?
Хотя люди знали о фи уже давно, большую известность он приобрел только в последние столетия.По словам Нотта, итальянский математик эпохи Возрождения Лука Пачоли написал книгу под названием «De Divina Proportione» («Божественная пропорция») в 1509 году, в которой обсуждалась и популяризовалась фи.
Пачоли использовал рисунки, сделанные Леонардо да Винчи , которые включали фи, и возможно, что да Винчи был первым, кто назвал его «sectio aurea» (латинское «золотое сечение»). Только в 1800-х годах американский математик Марк Барр использовал греческую букву Φ (фи) для обозначения этого числа.
Как свидетельствуют другие названия числа, такие как божественная пропорция и золотое сечение, фи приписывают множество чудесных свойств. Писатель Дэн Браун включил длинный отрывок в свой бестселлер «Код да Винчи» (Doubleday, 2000), в котором главный герой обсуждает, как фи представляет собой идеал красоты и встречается на протяжении всей истории. Более трезвые ученые обычно опровергают подобные утверждения.
Например, энтузиасты фи часто упоминают, что некоторые измерения Великой пирамиды в Гизе , такие как длина ее основания и / или высота, находятся в золотом сечении.Другие утверждают, что греки использовали фи при проектировании Парфенона или в своих прекрасных скульптурах.
Энтузиасты Пхи любят указывать на то, что пирамиды Гизы, построенные между 2589 и 2504 годами до нашей эры, были построены в золотом сечении. Но измерения по своей природе неточны и произвольны, поэтому пирамиды не являются точными примерами золотого сечения. (Изображение предоставлено Дэном Брекволдтом Shutterstock)Но, как Марковский указал в своей статье 1992 года в журнале College Mathematics Journal под названием «Заблуждения о золотом сечении»: «измерения реальных объектов могут быть только приблизительными.Поверхности реальных объектов никогда не бывают идеально плоскими ». Далее он написал, что неточности в точности измерений приводят к еще большим неточностям, когда эти измерения выражаются в соотношениях, поэтому заявления о древних зданиях или искусстве, соответствующих фи, должны приниматься с большой долей вероятности. крупица скепсиса
Часто говорят, что размеры архитектурных шедевров близки к фи, но, как отмечал Марковский, иногда это означает, что люди просто ищут соотношение, которое дает 1,6, и называют это фи.Найти два отрезка с соотношением 1,6 не составляет особого труда. Выбор места для измерения может быть произвольным и при необходимости отрегулирован, чтобы приблизить значения к фи.
Попытки найти фи в человеческом теле также поддаются подобным заблуждениям. В недавнем исследовании утверждалось, что золотое сечение обнаруживается в разных пропорциях человеческого черепа. Но, как сказал Live Science :
Дейл Риттер, ведущий преподаватель анатомии человека Медицинской школы Альперта (AMS) при Университете Брауна в Род-Айленде, сказал Live Science :
: ) наука в нем … с таким количеством костей и таким количеством интересных точек на этих костях, я мог бы предположить, что в другом месте в скелетной системе человека будет хотя бы несколько «золотых соотношений».
Связанный: Фотографии: большие числа, определяющие Вселенную
И хотя фи считается обычным явлением в природе, его значение преувеличено. Лепестки цветов часто имеют числа Фибоначчи, такие как пять или восемь, а сосновые шишки растут свои семена наружу по спирали чисел Фибоначчи. Но есть столько же растений, которые не следуют этому правилу, так и те, которые соблюдают, сказал Кейт Девлин, математик из Стэнфордского университета, Live Science .
Люди утверждали, что морские ракушки, такие как ракушки наутилуса, обладают свойствами, присущими фи.Но, как указывает Девлин на своем веб-сайте , «наутилус действительно наращивает свою раковину по логарифмической спирали, то есть спирали, которая поворачивается на постоянный угол по всей своей длине, что делает его везде самоподобным. постоянный угол — это не золотое сечение. Жалко, я знаю, но вот оно. »
Хотя фи, безусловно, представляет собой интересную математическую идею, именно мы, люди, придаем значение вещам, которые мы находим во Вселенной. Защитник, смотрящий через очки цвета фи, может повсюду видеть золотое сечение.Но всегда полезно выйти за рамки конкретной точки зрения и спросить, действительно ли мир соответствует нашему ограниченному пониманию.
Дополнительные ресурсы:
Последовательность Фибоначчи: примеры, золотое сечение и природа — видео и стенограмма урока
Золотое сечение
Золотое сечение , представленное греческой буквой фи, составляет примерно 1,618. Золотое сечение, как и Пи, — это иррациональное число, которое продолжает существовать.Фактическое значение выглядит так: 1.618033988764989. . .
Вам может быть интересно, как последовательность Фибоначчи соотносится с этим числом. Покажи нам.
Начнем с деления пар чисел в последовательности Фибоначчи. Мы пропустим ноль и начнем с пары единиц. 1/1 = 1. Следующая пара — это один и два. 2/1 = 2. В каждой паре мы делим большее на меньшее число. Давайте продолжим и посмотрим, куда это нас приведет:
| Пара Фибоначчи | Результат |
|---|---|
| 2 и 3 | 3/2 = 1.5 |
| 3 и 5 | 5/3 = 1,6666. . . |
| 5 и 8 | 8/5 = 1,6 |
| 8 и 13 | 13/8 = 1,625 |
| 13 и 21 | 21/13 = 1,6154. . . |
| 21 и 34 | 34/21 = 1,619. . . |
| 34 и 55 | 55/34 = 1,618. . . |
| 55 и 89 | 89/55 = 1.618.. . |
| 89 и 144 | 144/89 = 1,618. . . |
По мере того, как числа становятся больше, начинают происходить интересные вещи. Результат деления пар чисел дает приблизительное значение золотого сечения 1,618. . .
С математической точки зрения последовательность Фибоначчи сходится к по золотому сечению. Это означает, что по мере роста последовательности Фибоначчи, когда вы делите пару чисел из последовательности, результат будет становиться все ближе и ближе к фактическому значению золотого сечения.Посмотрев на таблицу, вы можете увидеть, что, начиная с пары 34 и 55, результат имеет точность до трех десятичных знаков. По мере того, как пары становятся больше, результат будет более точным до десятичной дроби.
Природа
Последовательность Фибоначчи приближается к золотому сечению, которое можно найти в мире природы. Вы можете увидеть это на собственном теле, в том, как растут ракушки, и в количестве лепестков в цветках. Давайте посмотрим на эти примеры из реальной жизни.
Взгляните на свои пальцы.Обратите внимание, что каждый палец состоит из трех частей. Если вы измерите каждую секцию и разделите пары секций, вы получите приблизительное значение золотого сечения. Если наименьшая часть вашего пальца измеряет одну единицу, то нижняя часть будет иметь размер примерно две единицы, а третья часть будет иметь размер примерно три единицы. Обратите внимание, как каждое измерение соответствует числу Фибоначчи.
Ракушки растут по последовательности Фибоначчи.Если вы выложите квадраты с размерами, соответствующими последовательности Фибоначчи (1, 1, 2, 3, 5 и т. Д.), И начертите спираль, которая соединяется с каждым внешним краем, вы увидите, как формируется морская ракушка.
Вы также увидите числа Фибоначчи в том, как цветы растут на своих лепестках. У орхидеи, например, несколько слоев лепестков, и каждый слой соответствует числу Фибоначчи. Посмотрите на изображение орхидеи, и вы увидите слой из двух лепестков, затем слой из трех лепестков, за которым следует внешний слой из пяти лепестков.
Резюме урока
Подводя итог, последовательность Фибоначчи начинается с 0 и 1, и каждое последующее число является суммой двух предыдущих чисел. По мере роста последовательности Фибоначчи, если вы разделите пары чисел в последовательности (большее на меньшее), вы получите приблизительное значение золотого сечения, которое составляет примерно 1,618.
Результаты обучения
Когда вы закончите, вы сможете:
- Описывать и идентифицировать последовательность Фибоначчи
- Объясните взаимосвязь между последовательностью Фибоначчи и золотым сечением
- Вспомните некоторые примеры последовательности Фибоначчи в природе
Последовательность Фибоначчи влияет на фондовый рынок | Наука
В пятницу, 20 марта, как U.Южный фондовый рынок завершил свою худшую неделю с 2008 года на фоне беспорядков, связанных с коронавирусом (до некоторого восстановления в начале следующей недели), перед инвесторами остался вопиющий вопрос: все ли идет под откос? В условиях такой экономической нестабильности некоторые исследователи рынка обращаются к знакомому мощному набору чисел для предсказания будущего.
«Коррекция Фибоначчи» — это инструмент, который технические аналитики используют для определения своих взглядов на поведение покупателей и продавцов на рынках.Этот метод назван в честь известной последовательности Фибоначчи, набора чисел, свойства которой связаны со многими природными явлениями. Хотя использование этих чисел для прогнозирования рыночных движений гораздо менее надежно, чем их использование для расчета структуры семян подсолнечника, появление последовательности в области финансов является еще одним свидетельством ее способности захватывать человеческое воображение.
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — это известная группа чисел, начинающаяся с 0 и 1, в которой каждое число является суммой двух перед ним.Он начинается с 0, 1, 1, 2, 3, 5, 8, 13, 21 и продолжается бесконечно. Шаблон скрывает мощный секрет: если вы разделите каждое число в последовательности на его предшественник (кроме 1, деленного на 0), то по мере продвижения к более высоким числам результат сходится к константе phi или приблизительно 1,61803, в противном случае известное как золотое сечение.
Последовательность имеет долгую историю. В Европе это было решение проблемы разведения кроликов, описанной в книге Liber Abaci итальянского математика Леонардо Пизанского в 1202 году A.Д. Но этот узор был известен в Индии гораздо раньше, возможно, даже в седьмом веке. Название последовательности происходит от прозвища Фибоначчи, что означает «сын Боначчи», данного Леонардо в 19 веке, согласно книге Кейта Девлина В поисках Фибоначчи: В поисках заново забытого математического гения, изменившего мир . Затем математик Эдуоард Лукас в 1870-х годах дал название «последовательность Фибоначчи» последовательности, полученной из сценария с кроликом.(Это также проявилось при подсчете количества пчел в последовательных поколениях).
Между тем, золотое сечение может быть записано как половина суммы 1 плюс квадратный корень из 5. И хотя фи не дает такого праздника с начинкой из теста, как пи, константа появляется в природных явлениях. Число спиралей в шишках — это числа Фибоначчи, как и количество лепестков в каждом слое определенных цветов. У спиралевидных растений каждый лист растет под углом по сравнению с его предшественником, равным 360 / phi 2 , и семена подсолнечника упакованы в спиралевидное образование в центре их цветка, геометрия которого также регулируется золотым сечением.
«Привлекательность золотого сечения проистекает в первую очередь из того факта, что оно имеет почти сверхъестественный способ появиться там, где его меньше всего ожидают», — пишет Марио Ливио в книге « Золотое сечение: история о Фи, самом удивительном числе в мире» . .
Но почему эта последовательность так повсеместна? «Многие вещи в математике и, вероятно, в реальном мире регулируются простыми рекурсивными правилами, где каждое вхождение регулируется простой формулой с точки зрения предыдущего вхождения», — сказал Кен Рибет, профессор математики Калифорнийского университета. Беркли.«И у числа Фибоначчи есть простейшая из возможных формул, просто сумма двух предыдущих».
Фибоначчи выходит на рынок
Люди запрограммированы на идентификацию закономерностей, и когда дело доходит до чисел Фибоначчи, мы не ограничиваемся поиском и восприятием последовательности в природе. Фибоначчи и фи можно найти в некоторых произведениях искусства, архитектуры и музыки (хотя это миф, что пирамиды Египта имеют к этому какое-то отношение).И хотя поведение покупателей и продавцов в значительной степени непредсказуемо, некоторые финансовые аналитики клянутся, что они тоже могут увидеть эти цифры в игре, в том числе в нынешнем экономическом кризисе.
Крупный план подсолнечника (Wiki Commons / Alex M3rcer)Инвестиционные исследователи, которых называют «техническими аналитиками», смотрят на исторические формы графиков, чтобы определить, будет ли текущая тенденция покупки или продажи продолжаться или измениться.Некоторые делают свои прогнозы, используя «уровни восстановления Фибоначчи», полученные из известной последовательности.
Технические аналитики могут смотреть на целый набор чисел, соответствующих соотношениям чисел в последовательности Фибоначчи, но пара важных из них — 61,8 процента и 38,2 процента. Любое данное число Фибоначчи, деленное на его преемник, составляет приблизительно 1 / фи, или 0,618. Число Фибоначчи, деленное на число на два разряда выше в последовательности, приблизительно равно 0.382.
Например, рассмотрим S&P 500. В разгар рецессии 2008 года индекс достиг своей самой низкой точки в 2009 году — 666 пунктов. С тех пор он, как правило, находится на длительном подъеме, достигнув пика в 3393 человека до резкого падения, вызванного коронавирусом в последние недели.
Чтобы понять тенденции нынешнего спада, Кэти Стоктон, основатель и управляющий партнер фирмы технического анализа Fairlead Strategies, LLC в Стэмфорде, штат Коннектикут, изучает, пробиваются ли ключевые индексы и акции через различные уровни.Если вы возьмете минимум 2009 года в 666 в качестве нижней (0 процентов) и максимум 2020 года в 3393 в качестве верхней (100 процентов), Стоктон будет следить за тем, закрывается ли S&P 500 две пятницы подряд ниже того, что она определяет как « уровень поддержки »38,2 процента. Этот уровень соответствует максимуму 3393 минус 1042 (38,2 процента разницы между максимумом и минимумом), что составляет 2351.
Пока что во время кризиса цены не падали так низко две пятницы подряд, хотя 20 марта индекс закрылся на мрачном уровне 2304.92. Если 27 марта цена закроется ниже этого уровня Фибоначчи 2351, это будет второй страйк подряд. Для таких аналитиков, как Стоктон, это будет указывать на то, что S&P рискует упасть ниже уровня 61,8%, или около 1708 года, что, согласно этой точке зрения, делает сейчас менее оптимальным временем для покупок.
Самореализующееся пророчество?
Рибет, математик, отвергает идею поиска паттернов, связанных с последовательностью Фибоначчи, для прогнозирования рынков.Но даже если это неправда, что числа Фибоначчи связаны с фундаментальными рыночными силами, рынки по своей природе реагируют на убеждения своих игроков. Так что, если инвесторы массово покупают из-за анализа Фибоначчи, они все равно создают восходящий тренд; аналогично для продажи.
Стоктон признает, что это, по крайней мере, частично объясняет движение золота в прошлом году, когда инвесторы внимательно отслеживали, поднимется ли цена унции выше определенного уровня Фибоначчи. Цены на золото значительно упали с 2012 по 2015 год, затем колебались в пределах от 1200 до 1400 долларов за унцию в течение четырех лет до июня 2019 года, когда, похоже, цена снова начала расти.
«Это был большой прорыв Фибоначчи, за которым наблюдали многие люди, даже до такой степени, что он стал настолько широко отслеживаемым уровнем, что, я думаю, он становится неким самореализующимся свойством», — сказал Стоктон.
Идея о том, что числа Фибоначчи управляют торговлей акциями людей, может быть волшебным мышлением, но достаточное количество людей с таким же магическим мышлением может двигать рынки. Готовясь к еще большему хаосу, мы, по крайней мере, можем успокоиться, зная, что сами числа Фибоначчи вечны.
Рекламное видео— Фибоначчи: это так же просто, как 1, 1, 2, 3
Добро пожаловать в мой курс по числам Фибоначчи и золотому сечению. Я стою здесь, в коридоре математического факультета моего университета, Гонконгского университета науки и технологий, и, как вы можете видеть, у нас есть прекрасное искусство, все математически связанное, но я думаю, что моя любимая картина — это вот здесь брат Лука Пачоли занимается математикой. Здесь он демонстрирует теорему Евклида, делая набросок этого 12-стороннего платонического тела, красивого кристалла, наполовину заполненного водой.Здесь вы можете увидеть линию воды. Причина, по которой я люблю эту картину, заключается в том, что этот монах действительно был человеком эпохи Возрождения, и он опубликовал книгу под названием «О божественной пропорции», которая посвящена золотому сечению. Иллюстрации в этой книге были выполнены Леонардо да Винчи, самым известным из деятелей эпохи Возрождения, и есть даже некоторые предположения, что эту картину также написал знаменитый Леонардо. Мой курс — это курс, который обычно не предлагается в университете, но у меня есть возможность представить его в Интернете просто для удовольствия.Я хочу действовать как куратор всей математики чисел Фибоначчи и золотого сечения. Если вы посмотрите в Интернете, вы можете найти много информации, а также много информации в университетской библиотеке. Итак, поехали. Я хочу показать вам увлекательную головоломку, которую любил Льюис Кэрролл, автор «Алисы в стране чудес». Передо мной стоит загадка под названием «обман Фибоначчи». Головоломка начинается с квадрата со сторонами 1, 2, 3, 4, 5, 6, 7, 8 на 1, 2, 3, 4, 5, 6, 7, 8.Квадрат восемь на восемь, так что в нем 64 таких маленьких коробочки. Я могу взять этот квадрат и переставить части. Итак, поместите трапецию снизу, поместите треугольник сверху, затем еще одну трапецию, а затем треугольник. Итак, я превратил этот квадрат в красивый прямоугольник. Стороны равны 1, 2, 3, 4, 5 на 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. Прямоугольник 5 на 13. Таким образом, количество маленьких коробок здесь 5 умножить на 13 равно 65. Итак, мы перешли от 64 маленьких коробок к 65 маленьким коробкам. Если бы я мог сделать это с золотом, то в результате получилась бы одна маленькая коробочка с золотом, так что я был бы чрезвычайно богатым человеком.Очевидно, я не могу этого сделать. Я обманул вас, поэтому это называется обманом Фибоначчи. Так что же особенного в размере квадрата и прямоугольника? У квадрата восемь сторон, у прямоугольника пять и 13. Пять, 8 и 13 — числа Фибоначчи. Между этими числами существует взаимосвязь, называемая идентичностью Кассини, которая вместе с золотым сечением может объяснить, как эта головоломка может вас обмануть. В этом курсе мы выясним личность Кассини, а также обсудим другие интересные математические отношения, которые связывают числа Фибоначчи и золотое сечение.Я также покажу вам, как построить, на мой взгляд, две самые красивые картинки в математике. Один ведет к спирали, называемой золотой спиралью, а другой — к другой спирали, называемой спиралью Фибоначчи. Фактически, я использую спираль Фибоначчи с первыми шестью числами Фибоначчи в качестве значка для этого курса. Посмотри на эту красивую картинку. Как я заинтересовался этой темой? Что ж, в моем университете я преподаю курс математической биологии, и в этом курсе я обсуждаю знаменитую задачу Фибоначчи о кролике, которая является одним из первых приложений математики в биологии.Я также говорю о том, как числа Фибоначчи могут неожиданно появляться в природе. Один из моих любимых примеров связан с расположением цветков; маленькие цветочки в головке подсолнуха. Числа Фибоначчи появляются как количество спиралей, видимых в голове, и их появление здесь связано с отношением к золотому сечению, этому особому числу, квадратному корню из 5 плюс 1, деленному на 2. Это иррациональное число, которое оказывается очень трудно аппроксимировать рациональным числом.Мы поговорим об этом более подробно в этом курсе. Так как же мне надеяться, что вы пройдете этот курс? Я надеюсь, что вы посмотрите все видео или объясните математику чисел Фибоначчи и золотого сечения, и я надеюсь, что вы попытаетесь решить некоторые проблемы, которые я поставлю в разделах обсуждения. Вам действительно нужно решать задачи, чтобы изучать математику. После того, как вы поработаете над проблемами, вы можете попробовать пройти тесты с несколькими вариантами ответов, которые я написал, чтобы проверить свои знания по материалам курса и задачам.Конечно, вы можете просто смотреть видео и наслаждаться курсом. Надеюсь, вам понравится этот курс.
Что такое золотое сечение?
Art by @tubikВдохновение живет вокруг нас, и каждый в мире всегда черпает разные идеи из искусства вокруг себя. Поэтому может показаться удивительным, что есть одно правило природы, которое проявляется вокруг нас так часто, что его изображали в самых печально известных произведениях искусства. Что общего у Моны Лизы, Великих пирамид Гизы, Парфенона и логотипа Apple? Все они либо выставлены, либо были разработаны с использованием золотого сечения.
Золотое сечение — это математическое соотношение, обнаруженное и обычно встречающееся в природе, но видимое почти везде, например, в архитектуре, музыке, живописи, современном дизайне и т. Д. При эффективном использовании он создает дизайн, который естественен и эстетичен для глаз благодаря своей композиции.
Так в чем же секрет этого волшебного соотношения? Давайте еще немного расскажем об этом математическом чуде. И давайте посмотрим, как вы можете использовать его для улучшения своих дизайнов.
Итак, что же такое золотое сечение?
Проще говоря, золотое сечение — это математическая формула, которая дает число 1,618.
Представьте себе прямоугольник, у которого, если вы отрезать квадрат, оставшийся прямоугольник будет иметь те же пропорции, что и исходный прямоугольник. Продолжая этот паттерн, вы получите диаграмму золотого сечения.Это число и само соотношение получены из последовательности Фибоначчи, которая представляет собой последовательность чисел, которые естественным образом встречаются в нашей среде.Но число также является решением квадратной формулы; в которые нам действительно не нужно сейчас вдаваться. Но вы, возможно, помните числа Фибоначчи из средней школы. Или из блокбастера середины 2000-х, который сводил всех с ума по святому Граалю, «Код да Винчи».
Помимо художественной литературы, в природе можно встретить золотое сечение. Вот почему ее еще называют «божественной пропорцией». Из-за его частоты в естественном мире. Количество лепестков на цветке часто является числом Фибоначчи.Семена сосновых шишек закручиваются по спирали чисел Фибоначчи. Даже количество сторон неочищенного банана обычно является числом Фибоначчи.
Теперь, когда мы освоились с концепцией, я уверен, что вы, ребята, не будете возражать, если захотите немного поторопиться. Спустимся в кроличью нору Фибоначчи.
Числа Фибоначчи — это последовательность, начинающаяся с 0 и 1, которая продолжается добавлением двух предыдущих чисел до бесконечности. Следовательно, последовательность выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21 и так далее.Это потому, что 0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5 и т. Д. Соотношения соседних чисел Фибоначчи (2/1, 3/2, 5/3 и т. Д.) Равны не совсем равны золотому сечению, но они приближаются к нему. Это означает, что чем выше число Фибоначчи, тем ближе их отношение к 1,618. Доля 5/3 уже довольно близка к 1,666666 …
Поскольку мы все дизайнеры, вероятно, легче понять эту концепцию визуально. Золотое сечение можно объяснить с помощью так называемого золотого прямоугольника.Прямоугольник с соотношением сторон 1: 618. Теперь представьте квадрат, высота и ширина которого равны размеру более короткого сегмента золотого прямоугольника. Если вы удалите этот квадрат, получившаяся форма будет иметь те же пропорции, что и исходный прямоугольник.
Таким образом, у вас остается другой золотой прямоугольник меньшего размера. Продолжая этот паттерн, вы получите диаграмму золотого сечения. Точно так же вы можете просто добавить квадрат рядом с золотым прямоугольником с длиной, равной высоте прямоугольника, и вы получите тот же эффект.
Теперь, начертив дугу окружности в каждом квадрате, мы получим Золотую спираль (также известную как спираль Дюрера). Еще одно естественное явление, проистекающее из самого соотношения.
Греческое происхождение золотого сечения
Известный греческий математик, которого называют «основателем геометрии», Евклид впервые упоминает это соотношение в своей работе «Элементы». ) свойство этого иррационального числа.
Источник: Unsplash Photo, отредактировано в Vectornator.
Но только 2000 лет спустя немецкий математик Мартин Ом дал ему «золотую» характеристику. И только в 20 веке греческая буква фи была фактически принята в качестве символа золотого сечения американским математиком Марком Барром. Он выбрал это конкретное письмо в память о греческом скульпторе Фидии, который, по признанию ряда искусствоведов, использовал золотое сечение во многих своих работах.Альтернативное обозначение — «тау», сокращение от греческого фолианта, означающего «резать». И это ссылка на «разделяющую» уместность, упомянутую выше.
Греки тоже заметили красоту этого соотношения. Они поняли, что «божественная пропорция» обеспечивает наиболее эстетичную композицию. Это представление было расширено в эпоху Возрождения известным итальянским математиком Леонардо да Винчи. Он иллюстрировал знаменитую книгу «De divina пропорционально» (Божественная пропорция), написанную Лукой Пачоли, монахом-францисканцем.В этой книге Пачоли пишет о математических и художественных пропорциях, а да Винчи набросал своего печально известного Витрувианского человека, чтобы проиллюстрировать, как даже человеческое тело уважает золотое сечение.
Но золотая пропорция встречается и во многих других контекстах. Хотя он получил свою известность в 16 веке, он использовался (сознательно или нет) задолго до этого. Возьмем, к примеру, Великую пирамиду в Гизе. Пропорция его длины и высоты — золотое сечение. Его пропорции также создают так называемый золотой треугольник.Хотя это не доказано, некоторые утверждают, что греческая архитектура была построена с использованием числа фи, включая Парфенон.
Фото Маркуса Списке на Unsplash.Как использовать золотое сечение в дизайне?
Этот краткий курс по математике, конечно, бесполезен, если вы не сможете успешно применить его в своей работе графического дизайна. Причина, по которой вы хотите применить это соотношение в своей работе, сводится к общей эстетике, которую вы хотите достичь.
Это соотношение позволяет создать ощущение естественной красоты, используя естественную гармонию и пропорции, наблюдаемые в окружающем нас мире.Даже наши лица следуют этому же соотношению. Нас так привлекает это соотношение, что в процессе эволюции человеческое восприятие естественным образом склоняется к желанию вещей, подсознательно демонстрирующих эту пропорцию золотого сечения. Анализ некоторых из самых желанных людей в шоу-бизнесе показал, что пропорции лица, которые ближе всего подходят к этому соотношению, имеют более высокий рейтинг по внешнему виду среди зрителей!
Когда дело доходит до дела, это соотношение дает фундаментальные знания, которые вам нужно знать при создании красивой композиции.Потому что это одна из ключевых целей дизайнера, верно? Создавать четкие и понятные макеты. Сбалансированные страницы с гармоничными пропорциями, содержащие информацию, которую легко читать и усваивать. Плавный дизайн иллюстраций.
Использование этих принципов, естественно, приведет к гораздо более целостному дизайну. Или, если подумать об этом с точки зрения UX, это приведет к лучшему взаимодействию с вашими пользователями.
Золотую спираль можно использовать с помощью нескольких инструментов в вашем дизайне, таких как сетки, правила интервалов, столбцы и желоба.Если вы иллюстрируете, попробуйте провести исследование известных природных элементов, которые имеют последовательность Фибоначчи, таких как волны, рога, сосновые шишки или даже форму нашей галактики. Если вы освоите ее, Золотая спираль может выглядеть в вашей работе особенно изящно, элегантно и даже эффектно; поскольку его путь ведет взгляд зрителя к важным частям вашего изображения.
Более конкретно, вот некоторые из способов использования пропорции золотого сечения и золотой спирали в ваших интересах.
1 — Типографика и общая иерархия дизайна
На первый взгляд может показаться, что типографика и математика не имеют ничего общего друг с другом. В конце концов, типографика состоит из букв, а математика — из чисел. В чем-то противоположны друг другу. Но правда в том, что типографика — это сочетание художественных форм букв и рациональных пропорций. Прекрасное сочетание формы и функции. Когда пропорции вашей типографики сбалансированы, вы действительно можете заставить ее гармонировать с вашим дизайном.
Вам необходимо учитывать три параметра текста: размер шрифта, высоту и ширину строки. Вместе эти измерения, которые мы воспринимаем по горизонтали или по вертикали, отвечают за то, как мы воспринимаем типографику. Между всеми тремя есть особые отношения. В частности, если ваша строка текста увеличивается в ширину, высота между строками также должна увеличиваться, чтобы улучшить ее читаемость. И как называются эти отношения? Соотношение.
Если вы используете какое-либо соотношение, почему бы не сделать его золотым? Снова и снова было доказано, что он улучшает эстетику всего, к чему прикасается.
Это соотношение может помочь вам определить размеры заголовков, основного текста и вспомогательного текста в ваших проектах.
Например, если ваш основной текст имеет размер 14 пикселей. Умножьте это на 1,618, вы получите 22,652. Это означает, что ваш заголовок должен иметь размер примерно 22/23 пикселя в соответствии с соотношением, чтобы естественным образом сбалансировать текст в теле ниже. Вы даже можете воспользоваться противоположным методом, чтобы определить размер основного текста, если вы зафиксировали размер заголовка.
2 — Редактирование и изменение размера изображений
Хотя легко определить, от какого белого пространства следует избавиться при кадрировании и изменении размера изображений, не забывайте, что впоследствии потребуется балансировка.
Обрезка во многом зависит от композиции вашего изображения. Сначала вам нужно подумать о некоторых ключевых вещах. Что является предметом визуального? Какие еще элементы вы можете включить в сцену? Есть ли на изображении естественные линии или кривые? Каким должен быть окончательный размер вашего холста?
Как только вы узнаете все ответы, у вас появится еще один вопрос. Вы хотите использовать сетку Фи или Золотую спираль?
Сетка Фи — это способ учитывать размерные отношения между элементами фотографии.Это похоже на Правило третей, но не так уж и упрощенно. Вы не разделяете кадр на 3 равных сегмента. Сетка имеет соотношение 1: 0,618: 1, так как центральные линии расположены ближе друг к другу. Линии сетки Фи создают визуально приятные пропорции, которые люди почти автоматически будут воспринимать как красивые. Если вы решите кадрировать с помощью сетки Фи, то ваш объект будет помещен ближе к центру изображения.
Со спиралью Фибоначчи структура вашей композиции совершенно другая.Если вы представите наложение спирали поверх изображения, область с наибольшим количеством деталей будет в самом маленьком прямоугольнике катушки. Но это не обязательно должно быть в углу. Это может быть где угодно в вашей композиции. Некоторые говорят, что лицо Моны Лизы также находится в этой важной области.
3 — Макет в дизайне пользовательского интерфейса
Использование этого соотношения также может помочь в разработке естественно привлекательного и успокаивающего пользовательского интерфейса за счет правильного привлечения внимания к важным вещам.
Кроме того, использовать золотое сечение в дизайнерской работе проще, чем вы думаете. Поскольку дизайн пользовательского интерфейса основан на логической композиции, вы можете использовать формулу в качестве инструмента для создания столбцов и пропорциональных макетов.
Например, предположим, вы хотите создать макет с боковой панелью шириной 1080 пикселей. Чтобы рассчитать ширину основного столбца, просто разделите 1080 пикселей на 1,618. В результате будет создан основной столбец шириной 667 пикселей. Вы хотите повторить тот же процесс для основного столбца, чтобы получить ширину боковой панели.Разделите 667 на 1,618, чтобы получить 412,5 пикселей.
Golden Canon Grid — Адриан Сомоса для Bont ™ в FreebiesНо, конечно, эти размеры не обязательно всегда использовать. Формула золотого сечения просто указывает на наиболее приятный баланс между областями вашего дизайна.
Фактически, теперь, когда вы это понимаете, вы можете увидеть этот хак в действии на многих веб-сайтах.
№4 — Дизайн логотипа
Twitter, Pepsi и Apple. Эти бренды и их логотипы в значительной степени вдохновлены золотым сечением, и некоторые использовали это соотношение во всем дизайне своего логотипа!
Любовь Apple к золотому сечению хорошо известна среди ее поклонников и в мире дизайна.Многие из их логотипов приложений навеяны этим соотношением, и логотип iCloud является ярким примером этого.
Отличный способ использования золотого сечения — это определить высоту и ширину логотипа, а также пропорции внутренних элементов всего дизайна.
Золотой прямоугольник также можно использовать для размещения объектов и определения наилучшей композиции, наиболее приятной для глаз. Используя его простую формулу, вы убедитесь, что все части вашего логотипа расположены гармонично.
Или раздеть Золотую спираль на запчасти! Вы можете использовать круги, определяющие Золотую спираль, как основу вашего логотипа.
Итак, в следующий раз, когда вы будете стремиться к прорыву в логотипе, почему бы не попробовать это удобное соотношение, которое можно найти в природе? Это откроет дверь к удивительным дизайнерским решениям и обострит вашу дизайнерскую чувствительность, чтобы применять простые дроби и пропорции в вашем творческом процессе. Логотип
Fox с золотым сечением от DAINOGO Последний шаг
Итак, сегодня мы научились всегда помнить о золотом сечении для любых дизайнерских проектов.Будь то логотип, презентация или даже когда вы делаете что-то настолько простое, как кадрирование изображения.
Теперь, когда вы освоили золотое сечение, хотите попробовать? Почему бы не опробовать это на Vectornator? Если вы ищете профессиональное, интуитивно понятное и простое в использовании программное обеспечение для графического дизайна, мы вас поддержим.
Покажите нам свои потрясающие дизайны, отправив их нам или отметив #vectornator в социальных сетях.
φ Золотое сечение ★ Фибоначчи
Это отрывок из книги «Мастер Фибоначчи: человек, изменивший математику».Все цитаты занесены в каталог на странице «Цитаты».
ЗОЛОТОЕ СООТНОШЕНИЕ
(Предыдущий раздел: Phi )
Купить сейчас на AmazonДревнее соотношение Евклида на протяжении веков описывалось многими именами, но впервые было названо «золотым сечением» в девятнадцатом веке. Не очевидно, что Фибоначчи установил какую-либо связь между этим соотношением и последовательностью чисел, которую он нашел в задаче о кролике («Евклид»). Только в конце семнадцатого века связь между числами Фибоначчи и золотым сечением была доказана (и даже тогда не полностью) шотландским математиком Робертом Симсоном (1687-1768) (Livio 101).
Греческая буква тау (Ττ) на протяжении сотен лет представляла золотое сечение в математике, но недавно (в начале 20-го века) американскому математику Марку Барру, который выбрал первое соотношение, был придан символ фи ( Φ ). Греческая буква в имени великого скульптора Фидия (ок. 490–430 до н. Э.), Потому что считалось, что он использовал золотое сечение в своих скульптурах и в дизайне Парфенона (Доннеган; Ливио 5). [Правдивость этих и других утверждений (например, о том, что золотое сечение встречается в картинах, пирамидах Египта и измерениях пропорций человеческого тела) рассматривается в книге «Фибоначчи в искусстве и музыке.»] Немецкий математик Мартин Ом (брат физика Георга Симона Ома, в честь которого назван закон Ома) впервые использовал термин« золотое сечение »для описания этого отношения во втором издании своей книги Die Reine Elementar-Mathematik (The Pure Элементарная математика) (1835). Он писал: «Это разделение произвольной линии на две такие части обычно называют« золотым сечением »». Однако он не изобретал этот термин, поскольку сказал «обычно называет», указывая на то, что этот термин является общепринятым. принял тот, который использовал сам (Livio 6).
Купить сейчас на AmazonЧисло золотого сечения для phi (φ) составляет 0,61803 39887…, что коррелирует с соотношением, вычисляемым при делении числа в ряду Фибоначчи на его последующее число, например 34/55, а также число, полученное при делении крайней части линии на целое. Это число является обратной величиной 1,61803 39887… или Phi (Φ), что является отношением, вычисляемым при делении числа в ряду Фибоначчи на предшествующее ему число, например, при делении 55/34 и при делении всей линии. по самому большому разделу.n) / (x — (1-x)), где x = (1 + sqrt 5) / 2 ~ 1,618.
Другой способ написать уравнение:
Следовательно, phi = 0,618 и 1 / Phi. Сила фи — это отрицательная сила фи. Одна из причин, по которой последовательность Фибоначчи очаровывала людей на протяжении веков, заключается в этой тенденции соотношения чисел в рядах падать либо на фи, либо на фи [после F (8)]. Другие обсуждали, может ли существовать сверхъестественное объяснение того, что кажется невероятным математическим совпадением.
Спираль Фибоначчи
Границы квадратов последовательных чисел Фибоначчи создают спираль, известную как спираль Фибоначчи; он следует за поворотами под постоянным углом, очень близким к золотому сечению. В результате ее часто называют золотой спиралью (Леви 121).
Золотая спиральИстинная золотая спираль образована серией золотых прямоугольников с одинаковыми пропорциями, поэтому она не совсем такая же, как спираль Фибоначчи, но очень похожа.По мере того, как спираль Фибоначчи увеличивается в размере, она приближается к углу золотой спирали, потому что отношение каждого числа в ряду Фибоначчи к числу до того, как оно сходится к Phi , 1,618 по мере развития ряда (Meisner, «Spirals »).
Купить сейчас на AmazonМногие природные явления (например, вращение ураганов и спиральные рукава галактик) и объекты в природе, кажется, существуют в форме золотых спиралей; например, раковина наутилуса с камерами (Nautilus pompilius) и расположение семян в головке подсолнечника, очевидно, расположены по спирали, как и чешуйки шишек сосновых шишек (Knott, Brief; Livio 8).Спирали Фибоначчи, золотые спирали и спирали, основанные на золотом сечении, часто появляются в живых организмах. Однако не каждая спираль в природе связана с числами Фибоначчи или Фи; некоторые из этих спиралей являются равноугольными спиралями, а не спиралями Фибоначчи или золотыми спиралями. Равноугольная спираль имеет уникальные математические свойства, при которых размер спирали увеличивается, но объект сохраняет форму кривой при каждом последующем повороте. Числа Фибоначчи чаще всего встречаются в природе в количестве и расположении листьев вокруг стеблей растений, а также в расположении листьев, частей и семян цветов и других растений (Мейснер, «Спирали»).
Многие наблюдатели находят паттерны спиралей Фибоначчи и золотых спиралей эстетически более привлекательными, чем другие паттерны. Поэтому некоторые историки и изучающие математику придают исключительную ценность тем объектам и видам деятельности в природе, которые, кажется, следуют паттернам Фибоначчи.
Тайны математики: Фибоначчи и золотое сечение
Я хотел поделиться по-настоящему увлекательным занятием, которое можно было бы превратить в столь же быстрое или столь продолжительное занятие или проект, как захотите.Он включает в себя два из того, что я называю «загадками математики», последовательность Фибоначчи и золотое сечение.Для тех из вас, кто не знает, последовательность Фибоначчи генерируется правилом сложения двух предыдущих чисел, чтобы получить третье и так далее. Самая известная версия этой последовательности генерируется, когда вы начинаете с чисел 1 и 1
Золотое сечение (также известное как греческая буква фи) — это иррациональное и трансцендентное число, которое приблизительно равно 1.6180339887. Один из способов получить золотое сечение — разделить большее число на меньшее в последовательности Фибоначчи (например, 5/3 = 1,66666, 13/8 = 1,625, 21/13 = 1,61538 и т. Д.). На языке вычислений можно сказать, что предел, когда количество членов в последовательности Фибоначчи приближается к бесконечности, отношение приближается к фи.
Итак, прежде чем я поговорил со студентами о последовательности Фибоначчи или золотом сечении, мы выполнили упражнение по измерению, в котором студенты измеряют различные части своего тела и вычисляют отношение большего к меньшему.После этого они индивидуально отправили свои данные в эту форму Google (если вы не используете эту удивительную и бесплатную технологию в своем классе по естествознанию и математике, узнайте, как это сделать на странице учебника по формам Google)
Я должен упомянуть, что я был вдохновлен сделать это задание после прочтения этой замечательной публикации в блоге Republic of Math.
Когда мы посмотрели на данные, мы изучили их средние данные по классу и индивидуальные данные и поняли, насколько они похожи. Мы поговорили о золотом сечении, и я показал им это видео на YouTube, в котором описывается, где можно найти золотое сечение в природе и в нашем мире.
Как я и надеялся, один из студентов спросил: «Почему наши данные не совпадают в точности с золотым сечением?» Некоторые студенты предположили, что это произошло из-за ошибки измерения. У другого студента была отличная идея, что, возможно, поскольку они подростки, которые все еще растут, возможно, это нарушает соотношение.
Я люблю такие дни, когда я могу отлично поговорить о природе науки и математики. В этих обсуждениях всплывают случайные темы, такие как Треугольник Паскаля и сколько сторон и / или вершин у круга.
Я спросил их, могут ли они придумать программу на питоне, которая могла бы предложить все числа Фибоначчи и золотое сечение, которые они хотели. Поскольку они еще не написали программу сами по себе, они изначально были в тупике, но на следующей неделе я покажу вам разговор, который в конечном итоге привел к их алгоритму и программе.
Подпишитесь на BrokenAirplane! .

 Форма подписки — под статьей.
Форма подписки — под статьей. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной. Можно рассчитать число Фибоначчи, умножив предыдущее число на золотое сечение (1,618), а затем округлив полученный результат.
Можно рассчитать число Фибоначчи, умножив предыдущее число на золотое сечение (1,618), а затем округлив полученный результат. Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.
Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.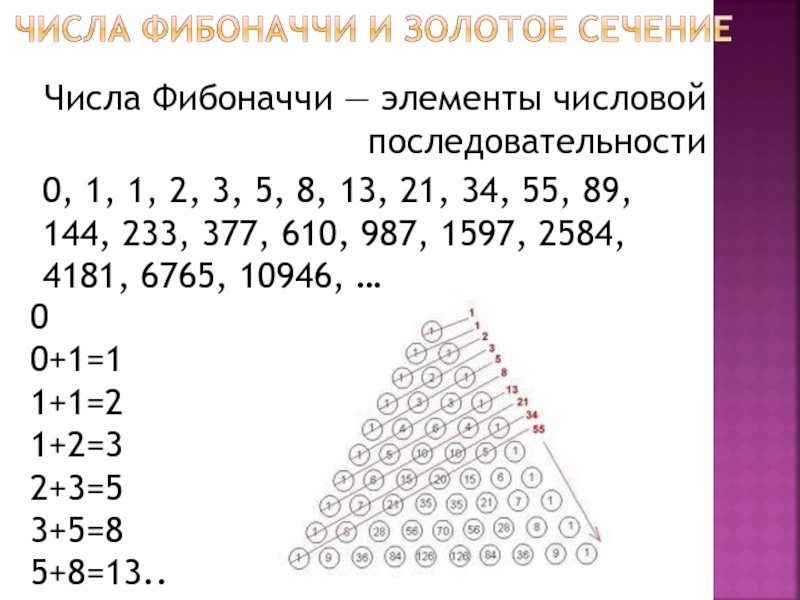
 Подобное соотношение можно встретить в следующих областях:
Подобное соотношение можно встретить в следующих областях:
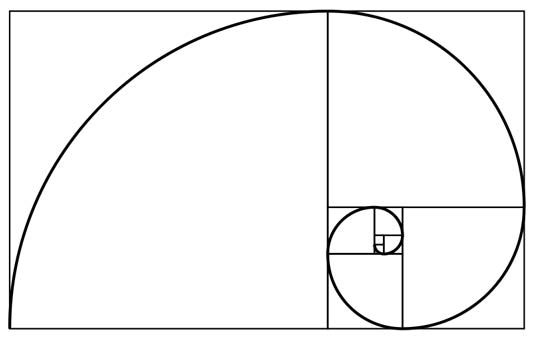 Аналогичная ситуация и с размером ладони, только в роли этого сечения выступает линия, проходящая через сустав между третьей и второй фалангой. Также считается, что изначально на подобные части, как в последовательности фибоначчи, делил тело пупок. Однако, со временем начались отклонения от этих значений, что объясняется эволюцией и приспособлением под окружающие человека условия.
Аналогичная ситуация и с размером ладони, только в роли этого сечения выступает линия, проходящая через сустав между третьей и второй фалангой. Также считается, что изначально на подобные части, как в последовательности фибоначчи, делил тело пупок. Однако, со временем начались отклонения от этих значений, что объясняется эволюцией и приспособлением под окружающие человека условия. Человеческое восприятие объектов, в которых есть такие соотношения ассоциируется с гармонией, что довольно странно на фоне восприятия симметричных объектов, как практически идеальных. Тем не менее, данный факт известен очень давно и активно применяется.
Человеческое восприятие объектов, в которых есть такие соотношения ассоциируется с гармонией, что довольно странно на фоне восприятия симметричных объектов, как практически идеальных. Тем не менее, данный факт известен очень давно и активно применяется.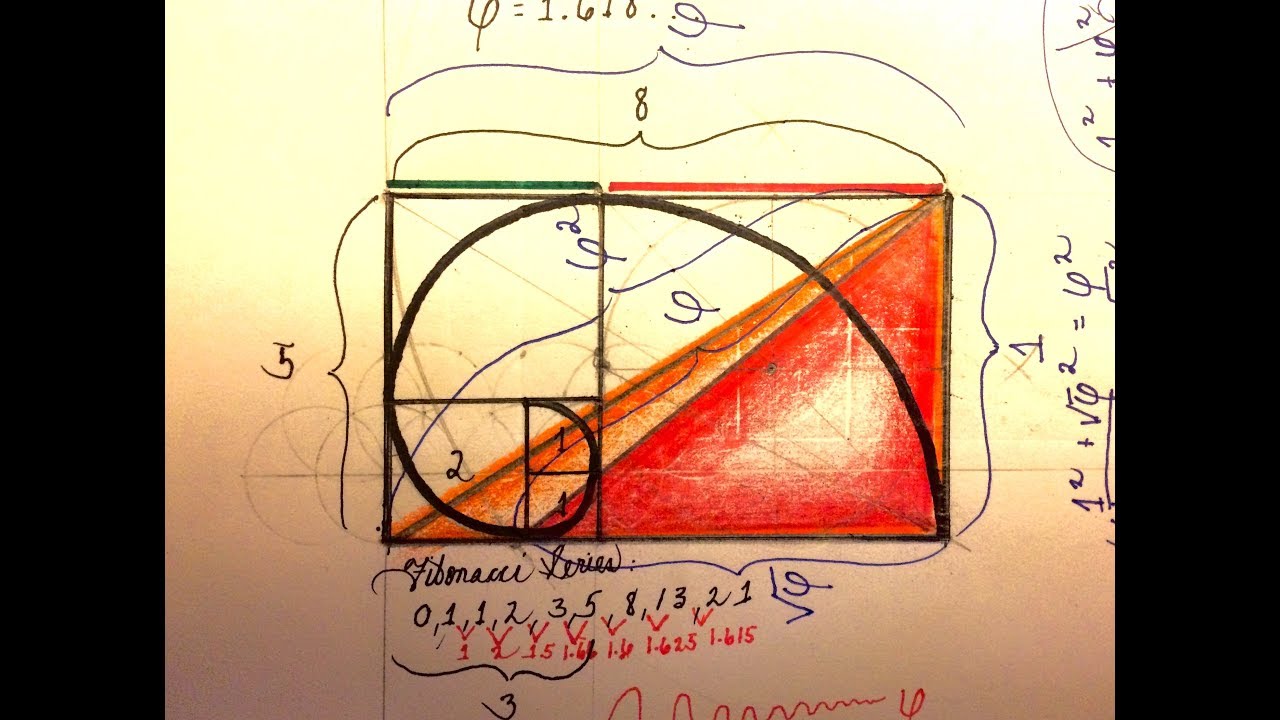 Число 1,618 можно заметить и в творчестве средневековья, и в современных произведениях архитектурного искусства.
Число 1,618 можно заметить и в творчестве средневековья, и в современных произведениях архитектурного искусства.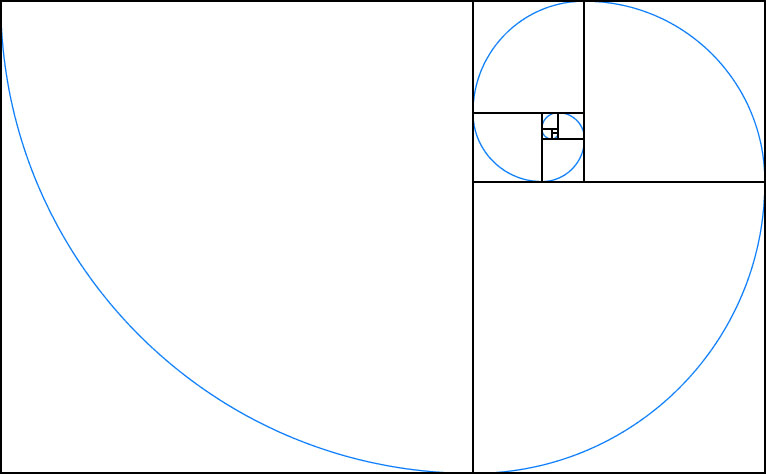 Пачоли ди Борго «Божественная пропорция» (1509 г.). В ней были приведены иллюстрации Леонардо да Винчи, который и закрепил новое название «золотое сечение». Также были научно доказаны 12 свойств золотой пропорции, причем автор рассказывал о том, как проявляется она в природе, в искусстве и называл ее «принципом построения мира и природы».
Пачоли ди Борго «Божественная пропорция» (1509 г.). В ней были приведены иллюстрации Леонардо да Винчи, который и закрепил новое название «золотое сечение». Также были научно доказаны 12 свойств золотой пропорции, причем автор рассказывал о том, как проявляется она в природе, в искусстве и называл ее «принципом построения мира и природы».