Матрицы: определение и основные понятия.
Навигация по странице:
Определение матрицы
Определение.
Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами.Количество строк и столбцов задают размеры матрицы.
Обозначение
Матрица — это таблица данных, которая берется в круглые скобки:
| A = | 4 | 1 | -7 | ||
| -1 | 0 | 2 |
Матрица обычно обозначаются заглавными буквами латинского алфавитв. Матрица содержащая n строк и m столбцов, называется матрицей размера n×m. При необходимости размер матрицы записывается следующим образом: An×m.
Элементы матрицы
Элементы матрицы A обозначаются aij, где i — номер строки, в которой находится элемент, j — номер столбца.
Пример.
Элементы матрицы A4×4:| A = | 4 | 1 | -7 | 2 | ||
| -1 | 0 | 2 | 44 | |||
| 4 | 6 | 7 | 9 | |||
| 11 | 3 | 1 | 5 |
a11 = 4
Определение.
Строка матрицы называется нулевой, если все ее элементы равны нулю.Определение.
Если хотя бы один из элементов строки матрицы не равен нулю, то строка называется ненулевой.Пример.
Демонстрация нулевых и ненулевых строк матрицы:| 4 | 1 | -7 | < не нулевая строка | ||
| 0 | 0 | 0 | < нулевая строка | ||
| 0 | 1 | 0 | < не нулевая строка |
Определение.
не не нулевой столбец
Диагонали матрицы
Определение.
Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний угол.Пример.
Демонстрация главной и побочной диагонали матрицы:| 0 | 1 | -7 | — главнаяпобочная диагональ | ||
| 0 | 0 | 2 |
| 0 | 1 | -7 | — главнаяпобочная диагональ | ||
| 0 | 0 | 2 | |||
| 8 | 2 | 9 |
Определение.
Следом матрицы называется сумма диагональных элементов матрицы.Обозначение.
След матрицы обозначается trA = a11 + a22 + … + ann.Как найти размерность матрицы
Матрица записывается в виде прямоугольной таблицы, состоящей из некоторого количества строк и столбцов, на пересечении которых располагаются элементы матрицы. Основное математическое применение матриц – решение систем линейных уравнений.Число столбцов и строк задают размерность матрицы. К примеру, таблица размерностью 5×6 имеет 5 строк и 6 столбцов. В общем случае, размерность матрицы записывается в виде m×n, где число m указывает на количество строк, n – столбцов.
Размерность матрицы важно учитывать при совершении алгебраических операций. Например, складывать можно матрицы только одного и того же размера. Операция сложения матриц с разной размерностью не определена.
Если массив имеет размерность m×n, его можно умножить на массив n×l. Число столбцов первой матрицы должно равняться числу строк второй, иначе операция умножения не будет определена.
Число столбцов первой матрицы должно равняться числу строк второй, иначе операция умножения не будет определена.
Размерность матрицы указывает на число уравнений в системе и количество переменных. Число строк совпадает с количеством уравнений, а за каждым столбцом закреплена своя переменная. Решение системы линейных уравнений «записано» в действиях над матрицами. Благодаря матричной системе записи становится возможным решать системы высоких порядков.
Если число строк равно числу столбцов, матрица называется квадратной. В ней можно выделить главную и побочную диагонали. Главная идет от левого верхнего угла к правому нижнему, побочная – от правого верхнего к левому нижнему.
Массивы размерностью m×1 или 1×n являются векторами. Также в виде вектора можно представить любую строку и любой столбец произвольной таблицы. Для таких матриц определены все операции над векторами.
Поменяв в матрице A строки и столбцы местами, можно получить транспонированную матрицу A(Т). Таким образом, при транспонировании размерность m×n перейдет в n×m.
В программировании для прямоугольной таблицы задается два индекса, один из которых пробегает длину всей строки, другой – длину всего столбца. При этом цикл для одного индекса помещен внутрь цикла для другого, за счет чего обеспечивается последовательное прохождение всей размерности матрицы.
Матрицы размерность — Справочник химика 21
Рассмотрим некоторые свойства и связи в матрицах Г и В. Напомним, что рангом матрицы называется максимальное Число линейно-независимых векторов — строк матрицы, и численно ранг матрицы равен порядку ее наивысшего ненулевого минора. Матрица размерности (В х X М) имеет полный ранг, если ее ранг совпадает с минимальным из чисел В, М, т. е. если выполняется условие rg Г = ш п(Д, М), Важнейшее свойство такой матрицы заключается в том, что она сохраняет свой ранг при любых достаточно малых возмущениях, а ее нормальное решение имеет непрерывный характер.
Техника нахождения элементов матрицы Г достаточно проста [12, 63]. В уравнении (3.28) разобьем атомную матрицу В по столбцам на две матрицы В и В так, чтобы их размерность была соответственно (ТУ X М— )] и т -1) X I]. Для дальнейших преобразований удобно представить для матрицы В условие сохранения в виде = 0. В свою очередь В х можно разбить еще на две матрицы и перегруппировать столбцы так, чтобы получить неособенную квадратную матрицу размерности [(ТУ — —I) X М — I)]. Тогда размерность оставшейся матрицы есть [(Л/ — I) X ]. Аналогично для матрицы получим две матрицы размерностей [(ЛГ — /) X П и [/ х Л соответственно. В матричной записи имеем
Показатели степеней у размерностей переменных объединяются в матрицу размерностей [c.88]
Последовательный подход. Вначале рассмотрим эту проблему применительно к последовательному подходу. Здесь уменьшение размерности задачи расчета ХТС достигается методами структурного анализа [47]. При этом решаются следующие задачи 1) в схеме выделяются комплексы — совокупности блоков охваченных обратными связями [3, с. 33] 2) определение внутри каждого комплекса оптимальной с точки зрения какого-либо критерия совокупности итерируемых переменных (II, 5). Обычно совокупность итерируемых переменных (II, 5) выбирается из условия, чтобы их суммарная размерность была минимальной. Положительные и отрицательные стороны такого выбора переменных (II, 5) обсуждаются в работе [3, с. 85]. Отметим здесь, что применительно к квазиньютоновским методам это более или менее оправдано, поскольку, как мы уже отмечали, можно считать при применении этих методов, что число итераций растет пропорционально размерности системы нелинейных уравнений. Уменьшаются требования и к размеру памяти, поскольку приходится хранить одну или две матрицы размерности fix/г.
Матрица, содержащая одну строку, т. е. размерности 1 X и, называется вектор-строкой, а матрица размерности и X 1, т. е. состоящая из одного столбца, называется вектор-столбцом. [c.229]
Отличительной особенностью большинства соотношений, используемых для расчета коэффициентов активности многокомпонентной смеси, является то, что они являются обобщением соответствующих соотношений для бинарных смесей. Поэтому коэффициенты этих соотношений определяются по экспериментальным равновесным данным соответствующих бинарных пар. Очевидно, для системы, содержащей к компонентов, коэффициенты будут представляться в простейшем случае матрицей размерности к X к.
Для решения покомпонентного материального баланса применяются те же алгоритмы, что и при решении задачи линеаризации, однако здесь элементы являются скалярными величинами, а не матрицами размерностью (2С + I) х (2С + 1). [c.262]
Базисной матрицей называется невырожденная матрица размерности т хт, образованная из т столбцов матрицы ограничений А.
Пусть (/ = 1, 2 г = 1,. . га) есть -обратные матрицы размерности I X га, удовлетворяющие соотношениям [c.67]
Пусть Nq = щ,. . Пд) — матрица размерности (п X д), столбцы которой образованы векторами и, (г = 1,. . д ). Примем, что ранг ее равен а. Алгоритм движения надо строить таким образом, чтобы поисковые направления р1 лежали внутри линейного многообразия Ьд. Очевидно, что этого можно достигнуть, образуя направления по формуле [c.192]
Здесь С = Фп, т+1-Ф , т+1 — матрица размерности (т + 1 X X т + 1) 5 = II Я,. . Я — матрица размерности (т + 1 X 1) а = 0,. . — матрица размерности (т + 1 X 1).
Таким образом, в представлении (XI,2) векторы г/( ) и являются клеточными матрицами размерностей соответственно и х1 и т х1. Как обычно, уравнения блоков должны быть дополнены уравнениями связей [c.230]
Пусть I — матрица размерности (2/7 Хт), столбцы которой являются базисом подпространства V. Тогда нужно вычислять матрицу V I, т.е. применять оператор V к /п векторам. [c.84]
Всиомним теперь, что часть компонент вектора 6 — заданные величины, равные перемещениям на и перенесем произведения их на соответствующие элементы матрицы К в правую часть системы уравнений (4.204) вспомним также, что уравнения, соответствующие узлам на незаконны и вычеркнем их из системы (4.203). В результате этих преобразований получим вторую систему уравнений с матрицей размерности 2Х (Л/в—М в), где Мин — количество лежащих на 8и вершин. Обозначим эту матрицу через [ ], она получается вычеркиванием строк и столбцов матрицы [X] с номерами 21—1 и 21, где I пробегает номера вершин на 5 (заметим, что программная реализация этого процесса достаточно проста).
Матрица [К], называемая глобальной матрицей жесткости, или просто матрицей жесткости системы, получается сложением локальных матриц жесткости [Я ] по следующему правилу сначала к нулевой матрице размерности МХМ добавляется матрица, в левом верхнем углу которой стоит локальная матрица жесткости 1-го элемента, к получившейся матрице добавляется матрица размерности NXN, ненулевые элементы которой расположены на пересечении 2-го и 3-го столбцов и 2-й и 3-й строк и равны соответствующим элементам локальной матрицы жесткости для
Для группы Сав существует только четыре разных набора матриц размерности 1 X 1, т. е. четыре НП типа Л а, В (табл. 19). [c.114]
Таким образом, матрицы представления Г суть унитарные матрицы. Можно доказать, что все возможные представления каждой группы О (в том числе и не обязательно группы точечной симметрии) эквивалентны ее унитарным представлениям, другими словами, при подходящем выборе базиса матрицы любого представления переходят в унитарные матрицы, а потому при рассмотрении представлений достаточно ограничиться лишь унитарными представлениями. Среди всех унитарных представлений всегда есть единичное, или полносимметричное, в котором каждому элементу группы отвечает одна и та же матрица размерности 1 х 1, а именно единица. [c.201]
Среди всех унитарных представлений всегда есть единичное, или полносимметричное, в котором каждому элементу группы отвечает одна и та же матрица размерности 1 х 1, а именно единица. [c.201]
Отсюда следует, что любой объект gi е Охарактеризуется матрицей размерности [т X 1]. Каждый элемент этой матрицы принимает значение из отрезка [О, 1]. Примером таких объектов могут служить отдельные изделия выпускаемой продукции, а свойствами — характеристики качества изделий. [c.25]
I — единичная матрица размерности 3 х 3), согласно соотношению [c.346]
Представлением группы называется гомоморфное ютображение данной группы на группу квадратных матриц. Размерность матриц называется размерностью представления. [c.20]
Допустим, что матрицы компенсации можно представить в виде В( = (Е( где Et — единичная матрица размерности/и fXWf. Разо- [c.81]
Следовательно, проатранство решений (2) представляет собой матрицу размерностью 6 х 4. [c.143]
В результате полного цикла моделирования за время Т будет получена симуляционная матрица размерности (N 5), где N-общее число повторов, возникших с самого качала работы модели. [c.69]
Matlab размерность матриц — CodeRoad
Это простой внешний продукт. крон не нужен (хотя он будет работать.) bsxfun-это дикий перебор, хотя и даст то, что вы просили. repmat неуместен, потому что, хотя он поможет вам делать то, что вы хотите, он реплицирует массивы в памяти, используя больше ресурсов, чем необходимо. (Избегайте использования неэффективных стилей программирования, когда в вашем распоряжении есть хорошие.)
Все, что вам нужно использовать, — это простой оператор*.
A-это вектор строк. B вектор столбца.
C = B*A
это даст результат C (i, j)=B(i)*A(j), что именно то, что вы ищете. Обратите внимание, что это работает, потому что B-это 3×1, а A-1×4, поэтому размеры «inner» B и A действительно соответствуют.
В MATLAB, IF вы не уверены, что что-то работает, попробуйте!
A = [1 2 3 4];
B = [1;2;3];
C = B*A
ans =
1 2 3 4
2 4 6 8
3 6 9 12
Посмотрите, что крон действительно работал, хотя я бы поспорил, что использование крона здесь, вероятно, менее эффективно, чем простое умножение внешнего продукта.
C = kron(B,A)
C =
1 2 3 4
2 4 6 8
3 6 9 12
Кроме того, bsxfun будет работать и здесь, хотя, поскольку мы используем общий инструмент для выполнения чего-то, что будет делать базовый оператор, я бы поспорил, что он немного менее эффективен.
C = bsxfun(@times,B,A)
C =
1 2 3 4
2 4 6 8
3 6 9 12
Выбор WORST-это repmat. Опять же, поскольку он искусственно воспроизводит векторы в памяти FIRST, он должен выйти и захватить большие куски памяти в случае больших векторов.
C = repmat(B,1,4).*repmat(A,3,1)
C =
1 2 3 4
2 4 6 8
3 6 9 12
Я полагаю, для полноты картины вы также могли бы использовать meshgrid или ndgrid. Посмотрите, что он делает именно то, что сделал repmat, но здесь он явно создает новые матрицы. Опять же, это плохой стиль программирования, когда есть хорошие инструменты, чтобы делать именно то, что вы хотите.
[BB,AA] = ndgrid(B,A)
BB =
1 1 1 1
2 2 2 2
3 3 3 3
AA =
1 2 3 4
1 2 3 4
1 2 3 4
C = BB.*AA
C =
1 2 3 4
2 4 6 8
3 6 9 12
Что вам нужно понять, так это то, почему каждый из этих инструментов был использован для работы и почему они отличаются.
Изменение размерности матриц, выбор значений из NumPy массивов по условию
До этого момента индексы и срезы использовать для извлечения подмножеств.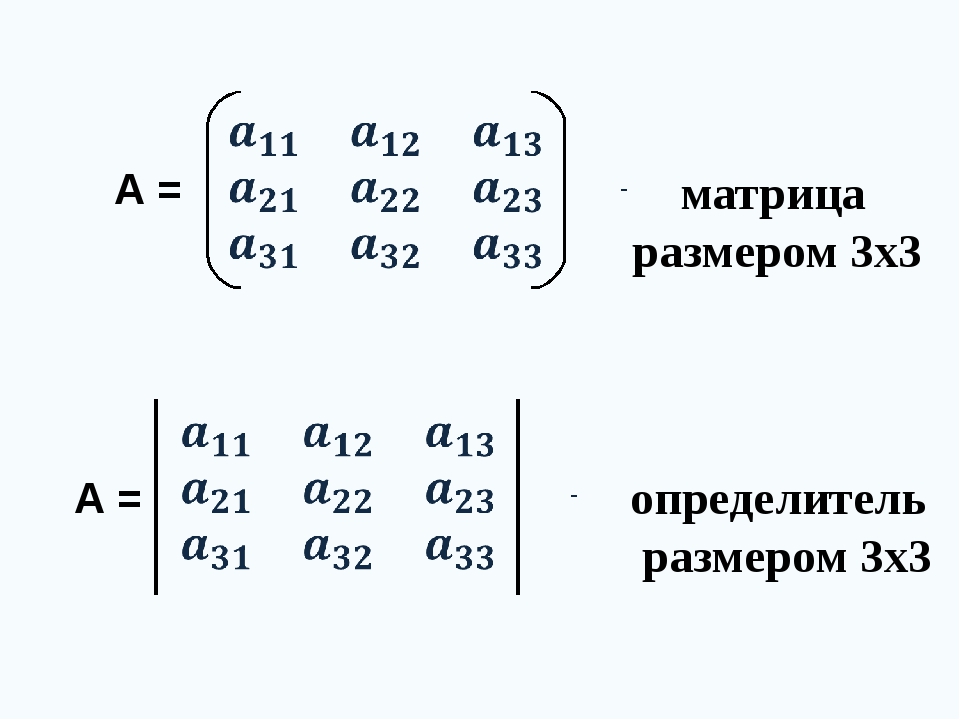 В этих методах используются числовые значения. Но есть альтернативный путь получения элементов — с помощью условий и булевых операторов.
В этих методах используются числовые значения. Но есть альтернативный путь получения элементов — с помощью условий и булевых операторов.
Предположим, что нужно выбрать все значения меньше 0,5 в матрице размером 4х4, которая содержит случайные значения между 0 и 1.
>>> A = np.random.random((4, 4))
>>> A
array([[ 0.03536295, 0.0035115 , 0.54742404, 0.68960999],
[ 0.21264709, 0.17121982, 0.81090212, 0.43408927],
[ 0.77116263, 0.04523647, 0.84632378, 0.54450749],
[ 0.86964585, 0.6470581 , 0.42582897, 0.22286282]])
Когда матрица из случайных значений определена, можно применить оператор условия. Результатом будет матрица из булевых значений: True, если элемент соответствовал условию и False — если нет. В этом примере можно видеть все элементы со значениями меньше 0,5.
>>> A < 0.5
array([[ True, True, False, False],
[ True, True, False, True],
[False, True, False, False],
[False, False, True, True]], dtype=bool)
На самом деле, булевы массивы используются для неявного извлечения частей массивов. Добавив прошлое условие в квадратные скобки, можно получить новый массив, который будет включать все элементы меньше 0,5 из предыдущего.
>>> A[A < 0.5]
array([ 0.03536295, 0.0035115 , 0.21264709, 0.17121982, 0.43408927,
0.04523647, 0.42582897, 0.22286282])
Управление размерностью
Вы уже видели, как можно превращать одномерный массив в матрицу с помощью функции reshape().
>>> a = np.random.random(12)
>>> a
array([ 0.77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
0.41894881, 0.73581471])
>>> A = a.reshape(3, 4)
>>> A
array([[ 0. 77841574, 0.39654203, 0.38188665, 0.26704305],
[ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
[ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])
77841574, 0.39654203, 0.38188665, 0.26704305],
[ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
[ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])
Функция reshape() возвращает новый массив и таким образом может создавать новые объекты. Но если необходимо изменить объект, поменяв его форму, нужно присвоить кортеж с новыми размерностями атрибуту shape массива.
>>> a.shape = (3, 4)
>>> a
array([[ 0.77841574, 0.39654203, 0.38188665, 0.26704305],
[ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
[ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])
Как видно на примере, в этот раз оригинальный массив изменил форму, и ничего не возвращается. Обратная операция также возможна. Можно конвертировать двухмерный массив в одномерный с помощью функции ravel().
>>> a = a.ravel()
array([ 0.77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
0.41894881, 0.73581471])
Или прямо повлиять на атрибут shape самого массива.
>>> a.shape = (12)
>>> a
array([ 0.77841574, 0.39654203, 0.38188665, 0.26704305, 0.27519705,
0.78115866, 0.96019214, 0.59328414, 0.52008642, 0.10862692,
0.41894881, 0.73581471])
Еще одна важная операция — транспонирование матрицы. Это инверсия колонок и рядов. NumPy предоставляет такую функциональность в функции transpose().
>>> A.transpose()
array([[ 0.77841574, 0.27519705, 0.52008642],
[ 0.39654203, 0.78115866, 0.10862692],
[ 0.38188665, 0.96019214, 0.41894881],
[ 0.26704305, 0.59328414, 0.73581471]])
Фрактальная размерность визуального образа математической матрицы Текст научной статьи по специальности «Математика»
Каштанов Николай Владимирович, Ляхов Александр Фёдорович
УДК 519. 633
633
ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ ВИЗУАЛЬНОГО ОБРАЗА МАТЕМАТИЧЕСКОЙ МАТРИЦЫ
Аннотация
В работе предлагается метод создания визуального образа числовой матрицы. Для его исследования вводится числовая характеристика ? фрактальная размерность, которая наряду с такими характеристиками как определитель матрицы и число обусловленности, позволяют делать заключения о качественных свойствах матрицы и решении соответствующих систем.
Ключевые слова: матрица, фрактальная размерность, определитель, число обусловленности.
Развитие современных информационных технологий позволяет создавать визуальные образы исследуемых объектов самой разной природы, осуществлять обработку этих образов и получать новую информацию как об объекте, так и об инструментах, с помощью которых производилось исследование.
В данной работе предлагается метод создания визуального образа числовой матрицы. Для его исследования вводится числовая характеристика — фрактальная размерность, которая наряду с такими характеристиками как определитель матрицы и число обусловленности, позволяет делать заключения о качественных свойствах матрицы и решении соответствующих систем.
ПОСТАНОВКА ЗАДАЧИ
При изучении систем линейных алгебраических уравнений большой размерности качественный анализ матрицы в виде боль© Каштанов Н.В., Ляхов А.Ф., 2013
шой числовой таблицы практически невозможен, поэтому возникает потребность визуализации матрицы. Для этого в работе используется графический метод: каждому из элементов матрицы системы ставится в соответствие ячейка, прямоугольник или пиксель определенного цвета. Градация цвета зависит от разброса значений элементов матрицы. Поскольку размеры пикселя малы, то таким способом на экране можно отобразить матрицу большой размерности.
Градация цвета зависит от разброса значений элементов матрицы. Поскольку размеры пикселя малы, то таким способом на экране можно отобразить матрицу большой размерности.
Визуальное представление матрицы позволяет сформулировать ряд новых задач:
1. Определить фрактальную размерность графического изображения матрицы
2. Определить, как изменяется фрактальная размерность матрицы при её преобразованиях.
В настоящее время при анализе и построении графических изображений широко используются фракталы и их различные виды [1-4].
Фрактал (от латинского /гаегш — дробленый, сломанный, разбитый) — термин, оз-
начающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа).
На практике, как правило, используется приближённая оценка фрактальной размерности множества.
На плоскости линейный размер множества точек и его площадь связаны. В качестве линейного размера множества возьмем его периметр. Предположим, что площадь и периметр связаны соотношением
S = PD,
где S и P — площадь и периметр1 множества, эти величины определяются из геометрии множеств, D — величина, являющаяся приближённой оценкой фрактальной размерности, которую в дальнейшем будем называть фрактальной характеристикой множества. Выразим D в явном виде: ^ lns
D =-. (1)
(1)
lnp kj
ОПРЕДЕЛЕНИЕ ФРАКТАЛЬНОЙ ХАРАКТЕРИСТИКИ МАТРИЦЫ С ПОМОЩЬЮ ПРОГРАММЫ IMAGEQ
Для определения фрактальной характеристики матрицы и её исследования в среде Microsoft Visual Studio 2005 на языке программирования С++ была написана программа ImageQ . Алгоритм программы и описание интерфейса приводится в приложении.
Программа позволяет сгенерировать квадратные числовые матрицы размерности, кратной степени 2 от (2 х 2) до (256 х256) и построить их визуальный образ. Для упрощения исследования визуальный образ матрицы строился в двух цветах. Положительные элементы матрицы изображаются чёрным цветом, отрицательные элементы -белым. На рис. 1 приведен скриншот про-
граммы. На рисунке показана сгенерированная матрица (8 х 8) и её визуальный образ, вычислены суммарная площадь черных пикселей, периметр, фрактальная размерность образа и число обусловленности матрицы.
Заметим, что программа позволяет вводить исследуемую матрицу в ручном режиме. Матрицу можно вводить поэлементно в соответствующее окно на форме, при этом изменяется её образ.
ИЗМЕНЕНИЕ ФРАКТАЛЬНОЙ РАЗМЕРНОСТИ ПРИ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЯХ МАТРИЦЫ
Определим диапазон изменения фрактальных характеристик сгенерированных матриц.
Площадь изображения определяется количеством положительных элементов матрицы n, то есть количеством чёрных пикселей. Площадь каждого пикселя Sp = 1, а периметр Pp= 4 . В этом случае площадь изображения S = N.
Периметр изображения будет лежать в следующих пределах. Максимальная длина границ изображения будет иметь место при условии, что каждый пиксель расположен отдельно: max P = 4 N = 4s.
Максимальная длина границ изображения будет иметь место при условии, что каждый пиксель расположен отдельно: max P = 4 N = 4s.
Минимальная длина границ будет иметь место при наиболее плотном расположении чёрных квадратов (рис. 2), то есть это будет
S
прямоугольник со сторонами [л[& ], —
_УS ]
и присоединенные к ним элементы S
s — [л/s ] •
<
_b/s ]
ют к периметру две единицы. Минимальный периметр
[л/s ], которые добавля-
minp = 2[*JS ] + 2
s
ь/s ]
+ 2 — 2S (S mod [VS ]).
Следовательно, фрактальная характеристика лежит в диапазоне
lns lns
ln(maxp)
< D <
ln(minp)
(2)
1 Под периметром множества понимается длина его границы.
Рис. 1
Приведём пример некоторых фрактальных характеристик для матриц часто встречающегося вида.
Единичная матрица размерности (8 х 8): её графический образ показан на рис. 3. S = 8, P = 32, Dim = 0,6, cond = 8 .
3. S = 8, P = 32, Dim = 0,6, cond = 8 .
На рис. 4 показан визуальный образ трёхдиаго-нальной матрицы и её характеристики. S = 22, P = 32, Dim = 0,89189632, cond = NaN (определитель матрицы равен нулю, то есть число обусловленности не существует).
Рис. 2. Фигура минимального периметра
Рис. 3
Рис. 4
На рис. 5 показан визуальный образ случайно сгенерированной матрицы (8 х 8) и её характеристики.
S = 22, P = 74, Dim = 0,71816181, cond = NaN.
Проведённые многочисленные эксперименты показывают, что для матриц с большим разбросом положительных и отрицательных элементов по матрице фрактальная характеристика матриц размерности (8 х 8) Dim » 0,72. Для матриц имеющих некоторую структуру, выражающуюся в заполне-
иии внутренних миноров матрицы однородными элементами, фрактальная характеристика матрицы значительно больше.
Предложенный анализ наиболее нагляден и полезен для сильно разряженных матриц, так как ненулевые элементы матрицы распределены по всей матрице, в этом случае фрактальная характеристика будет минимальной. Любое увеличение этой характеристики для таких матриц говорит о неоднородности их структуры.
Рис. 5
Заметим, что в приведённой последовательности примеров матриц единичная матрица имеет меньшее число элементов по сравнению с другими матрицами, и она может быть отнесена к сильно разрежённым матрицам.
При решении систем линейных уравнений и выполнении различных исследований, связанных с преобразованием матриц, наиболее часто используются линейные преобразования. При этих преобразованиях либо столбцы, либо строки матрицы умножаются на число, переставляются, складываются, вычитаются. Известно, что при этих преобразованиях определитель матрицы и число обусловленности изменяются.
При этих преобразованиях либо столбцы, либо строки матрицы умножаются на число, переставляются, складываются, вычитаются. Известно, что при этих преобразованиях определитель матрицы и число обусловленности изменяются.
Фрактальная характеристика матрицы также изменяется при линейных преобразованиях матрицы. Например, даже при перестановке строк будет происходить изменение контура фигур, визуализирующих элементы матриц, а площадь будет оставаться неизменной, то есть фрактальная характеристика изменится.
Заметим также, что при выполнении линейных преобразований изменяются численные соотношения между элементами матрицы, а при создании визуального образа происходит округление этих различий, и получаемые образы будут качественно отличаться.
Программа ImageQ позволяет сгенерировать матрицу, получить её образ и соответствующие характеристики, а затем получить образ матрицы, приведённой к треугольному виду. На рис. 6 приведены визуальный образ матрицы размерности 64 х 64 и образ матрицы после её приведения к треугольному виду. При этом значение фрактальной характеристики изменяется с 0,915 до 0,898.
На рис. 7 показана матрица размерности 256 х 256. Её фрактальная характеристика до преобразования Dim = 0,93712, после преобразований — Dim = 0,93336.
ЧИСЛО ОБУСЛОВЛЕННОСТЕЙ
МАТРИЦЫ И ХАРАКТЕРИСТИКА ИЗОБРАЖЕНИЯ
Программа ImageQ позволяет осуществлять многократное повторение численного эксперимента по генерации матрицы и вычисления ее характеристики. Поскольку в этом случае матрица генерируется случайным образом, то и соответствующее ей изображение, а значит и его характеристика случайны. При многократном повторении опыта, можно говорить о математическом ожидании и дисперсии случайной величины -характеристики изображения. Эти характеристики также определяются программой.
Эти характеристики также определяются программой.
Изменение математического ожидания М [П] фрактальной характеристики случайно сгенерированной матрицы с ростом её размерности п отражено на рис. 8.
Численные эксперименты по генерации матриц различного размера и подсчет их характеристик показывают, что с ростом размера матрицы существенно растет её число обусловленности. При этом характеристика соответствующего изображения приближается к 0,93. Для матриц небольшого разме-
Рис. 6
Рис. 7
Рис. 8
ра с малым числом обусловленностей характеристика составляет 0 -0,7. Результаты экспериментов приведены в табл. 1.
ЗАКЛЮЧЕНИЕ
Проведённые исследования показывают, что современные информационные технологии позволяют осуществлять визуализацию числовых матриц и исследование полученных образов. Фрактальная размерность изображения, наряду с такими характеристиками как определитель матрицы и число обусловленности, позволяют делать заключение о структуре и качественных свойствах матрицы и решении соответствующих систем.
Табл. 1. Рост числа обусловленностей и фрактальной размерности с ростом размера матриц
Размер Математическое ожидание Математическое ожидание
числа обусловленности фрактальной характеристики
2 2,29 0,528
4 37 0,6
8 149 0,845
16 69 0,859
32 723 0,89
64 991 0,912
128 3380 0,928
256 16000 0,9375
Приложение
ОПИСАНИЕ АЛГОРИТМА РАБОТЫ ПРОГРАММЫ IMAGEQ
Программа ImageQ написана в среде Microsoft Visual Studio 2005 на языке программирования С++. Программа состоит из двух базовых частей — класс «Матрица» и класс «Форма».
Программа состоит из двух базовых частей — класс «Матрица» и класс «Форма».
Первый обеспечивает удобство работы с числовыми матрицами, хранит их в памяти в виде таблиц и позволяет методами класса вычислять характеристики матрицы, а также проводить такие операции, как бинаризация.
Второй предназначен для визуального отображения интерфейса пользователя и представляет собой объект Windows::Forms. Имеет в своем составе меню управления и элементы для визуализации экспериментов.
Элемент PictureBox позволяет отображать на форме изображения различного размера и формата. При загрузке изображения с жесткого диска компьютера происходит построение массива бит в формате RGB, который используется для бинаризации исходного изображения. Для этого высчиты-вается среднее арифметическое каждой из компонент цвета для каждого пикселя и сравнивается с некоторым пороговым значением. В зависимости от результата сравнения происходит замена значений RGB компонент на {0, 0, 0}, что соответствует черному, либо на {255, 255, 255}, что соответствует белому цвету. Одновременно с этим происходит заполнение элементов матрицы значениями +1 или -1 в зависимости от цвета пикселя. Пиксель с координатами x, y соответствует x-столбцу и y-строке матрицы.
Рис. Интерфейс программы ImageQ
При запуске алгоритма подсчета характеристики изображения сначала подсчитывается число положительных элементов матрицы — это число равно площади множества на изображении, поскольку черные пиксели обозначены в матрице+1. Далее происходит перебор всех элементов матрицы и для каждого элемента, равного +1, подсчитывается количество граничных с ним элементов, равных -1. Это соответствует количеству переходов с черного пикселя на белый в изображении, то есть периметру множества. Дальнейший подсчет производится по формуле (3).
Дальнейший подсчет производится по формуле (3).
В случае запуска серии экспериментов происходит многократное повторение действий, описанных выше, и результат каждой итерации запоминается. Впоследствии по записанным результатам вычисляется экспериментальное математическое ожидание характеристики и ее дисперсия. Процесс выполнения серии экспериментов отображается при помощи ProgressBar.
Управление программой осуществляется при помощи основного меню формы. Для открытия изображения или загрузки матрицы необходимо выбрать пункт меню Файл®Открыть или Файл®3агрузить. В случае если выбранное в проводнике изображение не удовлетворяет поставленным требованиям (размер 256 на 256), то программа выдаст сообщение о некорректности входных данных. При удачном открытии изображения но будет отображено на форме. Для его бинаризации и подсчета характеристики следует в меню выбрать пункт Операции®Бинаризация и подсчет. Результаты работы программы будут выведены в соответствующие поля, а изображение будет преобразовано в черно-белое.
Для генерации матриц необходимо выбрать пункт Операции®Сгенерировать. При этом генерируются матрицы размерности, кратной степени двойки.
Для вывода характеристик сгенерированной матрицы и её бинаризированного изображения необходимо выбрать пункт Бинаризация и подсчет. Поставив галку в окно Use Table на соответствующем поле, получим численные значения сгенерированной матрицы. Следует заметить, что эти значения можно поэлементно менять.
Для запуска серии экспериментов необходимо ввести в поле Число экспериментов в серии количество желаемых экспериментов, а затем выбрать пункт меню Операции®Серия экспериментов. Процесс выполнения серии будет сопровождаться перерисовкой ProgressBar. После завершения
серии вычислений математическое ожидание характеристики изображения, его дисперсия, а также математическое ожидание числа обусловленности и его дисперсия будут выведены в соответствующие поля.
Для завершения работы программы следует выбрать пункт меню Файл®Выход. Желающие получить программу обращайтесь по электронному адресу: ALF [email protected]
Литература
1. Александров П.С., ПасынковБ.А. Введение в теорию размерности. М.: Наука 1973.
2. Кроновер P.M. Фракталы и хаос в динамических системах. Основы теории. М.: Постмаркет, 2003.
3. ТарасевичЮ.Ю. Перколяция: теория, приложения, алгоритмы / Учебное пособие М.: Едито-риал УРСС, 2002.
4. Морозов А.Д. Введение в теорию фракталов. Москва-Ижевск: Инстиут компьютерных исследований, 2002.
Abstract
This work represents research results of visual image of numeric matrices. Fractal dimension of matrix’s image can be used along with determinant and condition number to identify qualitative properties of the matrix.
Keywords: Matrix, fractal dimensionality, a determinant, number of conditionality.
Ляхов Александр Фёдорович, кандидат физико-математических наук, доцент кафедры теоретической механики механико-математи ческого факультета Нижегородского государственного университета им. Н.И. Лобачевского (Национального исследовательского университета), ЬуакИог@тт. ипп. ги,
Каштанов Николай Владимирович, магистр прикладной математики и информатики, инженер-программист ООО «Мера НН», [email protected]
© Наши авторы, 2013. Our authors, 2013.
Размер матрицы — Энциклопедия по экономике
Размеры матрицы можно существенно сократить за счет рассмотрения в ней лишь дефицитных материалов, оборудования, конструкций, т. е. таких, по которым
[c.101]
е. таких, по которым
[c.101]Решение. Размер матрицы произведения [c.260]
Равномерный закон распределения 34 Размер матрицы 2 Размерность пространства 270 Ранг 78 [c.304]
При больших размерах матрицы вычисление по этой формуле элементов матрицы А 1 требует громоздких расчетов. Поэтому изыскиваются различные более эффективные методы О.м. на ЭВМ. [c.233]
| Рис. 2. Окно диалога определения размеров матрицы |
Для размера матриц, отображающих re-мерное пространство в г-мер-ное, будем использовать обозначение ->г. [c.33]
Численное же нахождение оптимальных стратегий в матричных играх требует значительного объема вычислений, который быстро растет с увеличением размеров матрицы выигрышей игры. [c.59]
Матрицы — это массивы данных, имеющие прямоугольную форму. Данные располагаются в строках и столбцах. Размер матрицы выражается числом строк и столбцов, т.е. матрица с пятью строками и четырьмя столбцами будет матрицей размера 5×4. Например, следующая матрица имеет размер 3×3 [c.302]
Заметьте, что размер матрицы Z составляет только 2 2. Это потому, что размер матрицы-произведения равен числу строк в первой матрице и числу столбцов во второй. [c.304]
Все матрицы AS(t), AS(t — 1), S(At), S (At) квадратные и одинакового размера, т. е. имеют одинаковое количество строк и столбцов, определяемое числом участников игры. В нашем примере размеры матриц имеют число строк 3 + 1=4, где + 1 — это итоговая строка, число столбцов также 3 + 1 = 4, где + 1 — это итоговый столбец. Таким образом, размер матрицы (3 + 1) х (3 + 1) или 4 х 4. В общем же случае, при числе участников игры М размеры матриц с итогами будут соответственно (М + 1) х (М + 1). [c.17]
Число строк m и число столбцов в определяют размер матрицы, который обозначают как произведение числа строк на число столбцов mxn, и поэтому говорят матрица размером mxn. [c.364]
[c.364]
Размер матрицы является важнейшей характеристикой, определяющей вид матрицы и действия над ней. [c.364]
Произведение матриц (векторов) А, 10 и В10 1 также существует, так как внутренние индексы 10 и 10 совпадают, а размер матрицы-произведения будет 1 х 1, но это уже будет не матрица, а число (скаляр) j г [c.386]
Максимальный размер матрицы-корреспонденции определяется множеством плана счетов, точнее, мощностью этого множества — количеством счетов, содержащемся в плане. [c.391]
Только для синтетических счетов, содержащихся в плане, размер матрицы будет 76 х 76, а с субсчетами и произвольно устанавливаемыми субконто размер матрицы корреспонденции будет значительно большим, хотя матрица практически необозрима уже и в том случае, когда она имеет указанный размер 76 х 76. [c.391]
Множество использованных счетов в отчетном периоде (объединенное со счетами, которые имели ненулевое сальдо на начало периода) определяет минимальный размер матрицы-корреспонденции. [c.392]
Всего использовано 4 счета, поэтому минимальный размер матриц-корреспонденций и матриц-проводок 4×4. Матриц-проводок будет столько же, сколько и самих проводок. Они приводятся ниже [c.394]
Матрицы, пуансоны формовочных, вырубных, вытяжных штампов ковочные штампы и прессформы сложного профиля с полированием в размер матрицы для прессформ — растачивания сферических гнезд по шаблону. [c.357]
Текст программы оценки значимости экономических показателей приводится в приложении 2. Исходной информацией программы являются веса экспертов и матрицы экспертных заключений о весомости показателей. С ЭВМ поступают следующие сообщения веса экспертов, матрицы показателей, нормированные относительные веса. Правильность расчета проверяется условием сумма относительных весов показателей равна единице . Необходимые инструктивные материалы по подготовке исходных данных и работе с программой содержатся в источнике [63, с. 130—131]. Процедура проведения экспертной оценки показателей отличается простотой.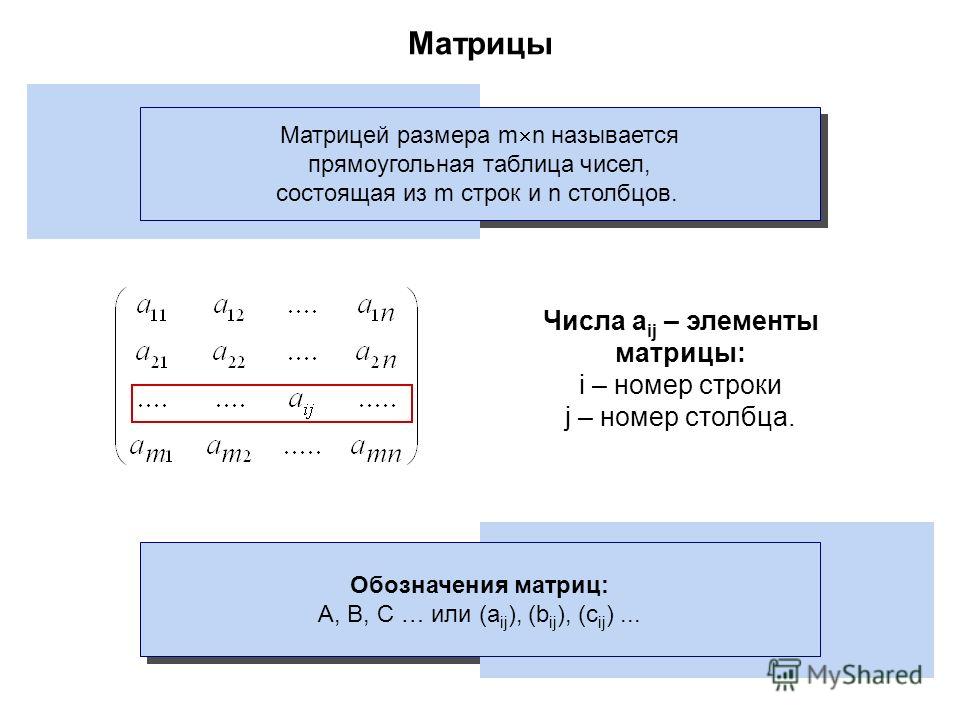 Она позволяет получить научно обоснованное коллективное заключение о сравнительной важности показателей. Каждый член экспертной группы заполняет матрицу. Размер матрицы зависит от числа ранжируемых показателей 3X3, 4X4, 5X5 и т. д. Используется метод парных сравнений. Если, по мнению эксперта, значимость показателей эквивалентна, им присваивается по 1 баллу, если один показатель более важен, чем другой,— 2 балла, менее важен —0 баллов.
[c.73]
Она позволяет получить научно обоснованное коллективное заключение о сравнительной важности показателей. Каждый член экспертной группы заполняет матрицу. Размер матрицы зависит от числа ранжируемых показателей 3X3, 4X4, 5X5 и т. д. Используется метод парных сравнений. Если, по мнению эксперта, значимость показателей эквивалентна, им присваивается по 1 баллу, если один показатель более важен, чем другой,— 2 балла, менее важен —0 баллов.
[c.73]
Модель (1) состоит из N блоков со следующими размерами матрицы каждого блока число столбцов — а = /n(./V + I) -f Jn (Pn + 1) число строк — Ъп — M — — pln + Jn(Рп + Q) + Кп [c.363]
Однако составление общей матрицы синтетического учета на ЭВМ и ее практическое применение связано с определенными трудностями. Если бухгалтерских сче тов имеется много, то соответственно и размеры матрицы крупные. При этом в матрице превалируют нулевые элементы, так как по общему правилу количество корреспондирующих счетов ограничено. В нашем примере нулевые элементы составляют от общего количества элементов матрицы 84%. По типовому счетному плану этот показатель составляет 73%, а по счетному плану ГЕНСИС —примерно 66% (см. 3.3). [c.83]
Размеры матрицы групп счетов небольшие. Нулевых элементов в этих матрицах встречается немного (всего 9), так как взаимосвязи счетов одной группы, как правило, в несколько раз теснее, чем взаимосвязи всех счетов (табл. 4.4). Нулевые элементы встречаются у раздела основных средств — по выходу с пятью и по вводу с тремя разделами. Отсутствует также связь между разделами денежных средств и затрат на производство. Более обоснованные частные матрицы можно конструировать на базе общей матрицы корреспонденции синтетических счетов, сгруппировав их согласно конкретным целям. [c.87]
Для измерения силы бизнеса могут быть использованы следующие переменные доля рынка, рост доли рынка, относительная доля рынка по отношению к ведущей марке, лидерство в качестве или другие характеристики, такие, как, например, издержки, прибыльность по отношению к лидеру. При определении размера матриц очень важную роль играет выбор единиц измерения объемов, норм приведения к единой базе, временных интервалов и т. д.
[c.173]
При определении размера матриц очень важную роль играет выбор единиц измерения объемов, норм приведения к единой базе, временных интервалов и т. д.
[c.173]
Разрыв между верхними и нижними уровнями в организации По матричной схеме работают нижние звенья, а «верхи» ею не пользуются Необходимо поддерживать маленький размер «матриц», чтобы вовлечь высшее руководство [c.269]
Большое значение имеет и другой параметр светочувствительной матрицы, про который обычно не упоминают, а именно — физический размер матрицы, от которого зависит и размер одной точки матрицы. Тут чем больше, тем лучше, так как больший по размеру пиксель может [c.305]
Смысл этого определения состоит в том, что доминирующая стратегия никогда не хуже, а в некоторых случаях даже лучше, чем доминируемая стратегия. Отсюда следует, что игроку нет необходимости использовать доминируемую стратегию. В самом деле, будут существовать оптимальные смешанные стратегии, при которых вероятность использования доминируемых строк и столбцов равна нулю, и при решении игры все доминируемые строки и столбцы могут быть отброшены, что позволяет уменьшить размеры матрицы. (Этот подход может использоваться также при поиске решения игры в чистых стратегиях.) [c.226]
Объем выборки m Объем данных по фактору (размер матрицы по вертикали). Применяется для установления тенденций изменения фактора Не менее чем в 3 — 5 раз больше числа факторов (nxj). С увеличением числа факторов кратность должна увеличиваться [c.321]
Критерий Фишера F Математический критерий, характеризующий значимость уравнения регрессии. Применяется для выбора модели Больше табличного значения, установленного для различных размеров матрицы и вероятностей [c.322]
Еще недавно категория матричных шрифтов являлась единственной. Шрифты в этом случае создаются по так называемой bitmap технологии, или методом битовой карты. В файле с таким шрифтом хранятся точечные изображения каждого символа внутри сетки точек фиксированного размера. Чем выше разрешающая способность устройства, тем больше размер матрицы, а стало быть и качество прорисовки контуров символов. Каждый символ растрового шрифта прорисовывается вручную и его форму можно подобрать так, чтобы он выглядел наилучшим образом на конкретном дисплее или при определенном разрешении. Однако разрешение обычного монитора намного хуже, чем разрешение самого слабого принтера. По этой причине нельзя добиться полного соответствия изображения на бумаге и на принтере. К недостаткам растровых шрифтов можно отнести существенное ухудшение качества изображения при изменении размера шрифта, его масштабировании. Контуры букв приобретают ступенчатую форму, возникает так называемый лестничный эффект. Принцип соответствия изображения WYSIWYG поддерживает большинство современных систем подготовки текстовой информации, поэтому возникает необходимость использования иной технологии создания шрифтов, свободной от указанных недостатков.
[c.408]
Чем выше разрешающая способность устройства, тем больше размер матрицы, а стало быть и качество прорисовки контуров символов. Каждый символ растрового шрифта прорисовывается вручную и его форму можно подобрать так, чтобы он выглядел наилучшим образом на конкретном дисплее или при определенном разрешении. Однако разрешение обычного монитора намного хуже, чем разрешение самого слабого принтера. По этой причине нельзя добиться полного соответствия изображения на бумаге и на принтере. К недостаткам растровых шрифтов можно отнести существенное ухудшение качества изображения при изменении размера шрифта, его масштабировании. Контуры букв приобретают ступенчатую форму, возникает так называемый лестничный эффект. Принцип соответствия изображения WYSIWYG поддерживает большинство современных систем подготовки текстовой информации, поэтому возникает необходимость использования иной технологии создания шрифтов, свободной от указанных недостатков.
[c.408]
Заданные подобным образом матрицы не имеют имен. Если вы хотите ввести матрицу, имеющую имя, необходимо сначала задать имя матрицы, затем ввести двоеточие. В результате после введенного вами неполного определения появится пустая ячейка. Затем следует открыть диалоговое окно создания матрицы любым из вышеперечисленных способов, задать в нем размеры матрицы и щелкнуть на кнопке Insert (Вставить) или ОК. Будет сгенерирована матрица, уже обладающая именем. Чтобы завершить определение необходимо, разумеется, еще ввести элементы матрицы. [c.48]
Указание. Для определения символьной матрицы введите с клавиатуры ее имя, символьный знак равенства (нажмите на клавиатуре одновременно клавиши и — на экране будет отображен знак равенства), определите размеры матрицы и введите ее элементы. Ввести букву греческого алфавита можно, щелкнув по кнопке с нужной буквой в панели [c.59]
Типовыми регионами являются город с населением около 1 млн. чел. (матрица 150×150), республика, край, область средних размеров (матрица 100×100), административный район с населением 50 тыс. чел. (матрица 60×60). Затраты на решение задач приведены в табл. 4.2.6.
[c.171]
чел. (матрица 60×60). Затраты на решение задач приведены в табл. 4.2.6.
[c.171]
Тщательный учет всех названных факторов фиксации размеров матриц ифает исключительно важную роль для качественного проведения анализа портфеля бизнесов. [c.104]
Введение в матрицы / Размер матрицы
Введение в Матрицы / Размер матрицы (стр. 1 из 3)
Разделы: Дополненные и коэффициенты матрицы / Размер матрицы, Обозначение матрицы и типы, Матричное равенство
Дополненный матрицы
Матрицы невероятно полезные вещи, которые возникают во многих различных прикладных областях.А пока вы наверное, только простейшие манипуляции с матрицами, а потом вы перейдете к следующей теме. Но не стоит удивляться, встретив матрицы опять же, скажем, в физике или технике. (Множественное число «матрицы» произносится как «MAY-truh-seez».)
Матрицы изначально были на основе систем линейных уравнений.
- Учитывая следующее систему уравнений, напишите соответствующую расширенную матрицу.
Запишите коэффициенты. и значения ответов, включая все знаки «минус». Если здесь — коэффициент «нет», тогда коэффициент равен «1».
То есть, учитывая систему (линейных) уравнений, вы можете связать с ним матрицу (сетку чисел внутри скобок), который содержит только коэффициенты линейного система. Это называется «расширенной матрицей»: сетка, содержащая коэффициенты из левой части каждого уравнения были «дополнены» с ответами из правой части каждого уравнения.
Записи (то есть
значения в) матрице соответствуют x -, л —
и z -значения
в исходной системе, если исходная система устроена правильно
в первую очередь. Иногда вам нужно переставить термины или вставить
нули в качестве заполнителей в вашей матрице.
Иногда вам нужно переставить термины или вставить
нули в качестве заполнителей в вашей матрице.
- Учитывая следующее систему уравнений, напишите соответствующую расширенную матрицу.
Мне сначала нужно переставить система как:
Тогда я могу написать
связанная матрица как:
При формировании дополненной матрица, используйте ноль для любой записи, где соответствующее место в системе линейных уравнений пусто.
Коэффициент матрицы
Если сформировать матрицу только по значениям коэффициентов матрица будет выглядеть так:
Это называется » матрица коэффициентов «.Авторские права Элизабет Стапель 2003-2011 Все права защищены
Выше мы пошли от линейного систему в расширенную матрицу. Вы можете пойти и другим путем.
- Учитывая следующее дополненная матрица, напишите связанную линейную систему.
Помните, что матрицы требуют, чтобы все переменные были выстроены аккуратно и аккуратно. И это обычно, когда у вас есть три переменные, использовать x , л , г. и z , в этой последовательности.Таким образом, соответствующая линейная система должна быть:
Размер матрицы
Матрицы часто упоминаются по их размерам. Размер матрицы задается в виде измерения, примерно так же, как комнату можно назвать «комнатой десять на двенадцать». Размеры матрицы — это строки и столбцы, а не размер ширина и длина. Например, рассмотрим следующую матрицу A :
Начиная с A имеет три ряда и четыре столбца ,
размер А это 3 4
(произносится как «три на четыре»).
Ряды идут бок о бок; столбцы идут вверх и вниз. «Строка» и «столбец» — это технические термины и не взаимозаменяемы. Размеры матрицы всегда задается сначала количеством строк, а затем количеством столбцов. Следуя этому соглашению, следующая матрица B :
… это 2 3. Если матрица имеет такое же количество строк, что и столбцы, матрица называется «квадратной». матрица.Например, матрица коэффициентов сверху:
… это 3 3 квадратная матрица.
Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
Цитируйте эту статью как: | Стапель, Елизавета.
«Введение в матрицы / размер матрицы.« Purplemath .
Доступно по номеру |
Размер матрицы — обзор
Для обозначения матрицы используется одна заглавная буква (или нижний индекс), выделенная жирным шрифтом (например, A , B , C 1 , C 2 ) в отличие от строчных полужирных букв, используемых для обозначения векторов.Заглавные буквы I и O обычно зарезервированы для специальных типов матриц, обсуждаемых позже.
Размер матрицы всегда указывается первым числом строк. Например, матрица 3 × 4 всегда имеет три строки и четыре столбца, а не четыре строки и три столбца.
Матрица m × n может рассматриваться либо как набор из m векторов-строк, каждый из которых имеет координаты n , либо как набор из n векторов-столбцов, каждый с координатами м . Матрица с одной строкой (или столбцом) по существу эквивалентна вектору с координатами в виде строки (или столбца).
Матрица с одной строкой (или столбцом) по существу эквивалентна вектору с координатами в виде строки (или столбца).
Мы часто пишем a ij для представления записи в строке i и j -м столбце матрицы A . Например, в предыдущей матрице A , a 23 — это запись -5 во второй строке и третьем столбце. Типичная матрица 3 × 4 C имеет элементы, обозначенные как
C = [c11c12c13c14c21c22c23c24c31c32c33c34].
ℳ mn представляет собой набор всех матриц с записями действительных чисел, имеющими m строк и n столбцов. Например, ℳ 34 — это набор всех матриц, имеющих три строки и четыре столбца. Типичная матрица в ℳ 34 имеет форму предыдущей матрицы C .
Основная диагональ элементов матрицы A — это a 11 , a 22 , a 33 ,…, те, которые лежат на диагональной линии рисуются вправо, начиная с верхнего левого угла матрицы.
Матрицы сложения и вычитания — ChiliMath
В этом уроке я подготовил семь (7) рабочих примеров, чтобы проиллюстрировать базовый подход к тому, как легко складывать или вычитать матрицы.
Если вы знаете, как складывать и вычитать действительные числа, эта тема должна быть действительно легкой. Единственное, что требуется для «легального» выполнения операций сложения или вычитания в «мире» матриц, — это убедиться, что данные матрицы должны иметь одинаковый размер или размерность.
Что означает, что данная матрица имеет одинаковый размер или размерность?
Предположим, нам даны матрицы A и B. Они имеют одинаковый размер или размер, потому что у них одинаковое количество строк и столбцов.
Мы можем описать размер или размерность матрицы, используя следующий стандартный формат:
количество строк x количество столбцов
Позвольте мне показать вам несколько примеров…
Последняя матрица размером 5 x 5 также считается «квадратной матрицей», потому что количество строк и количество столбцов равны.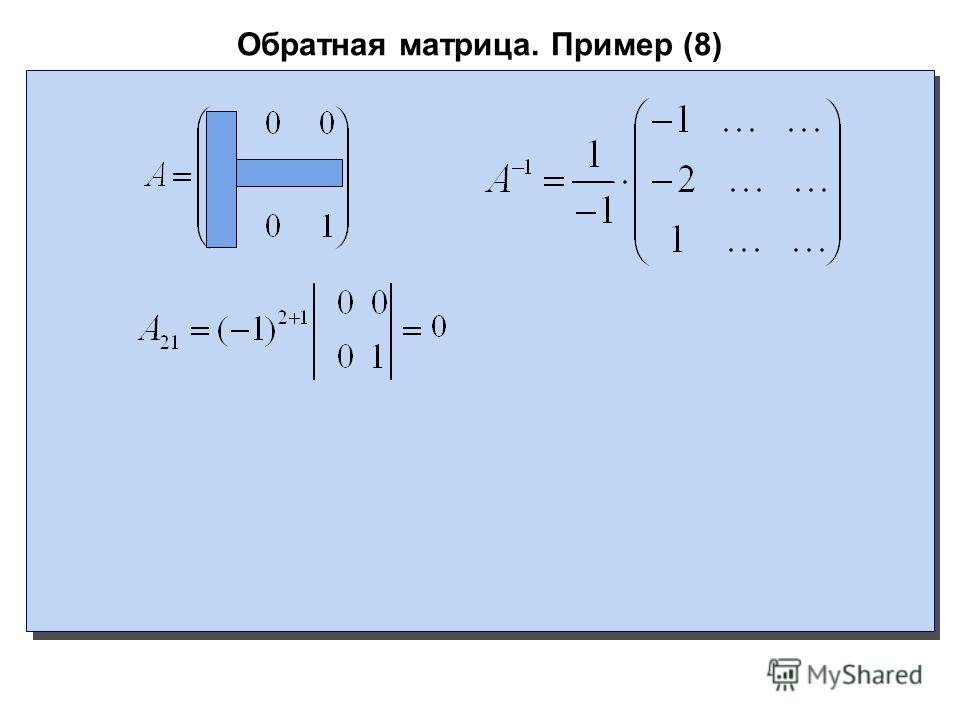 Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что все квадратные матрицы имеют обратные, но первое требование к матрице, чтобы иметь обратную матрицу, — это то, что сначала она должна быть квадратной матрицей.
Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что все квадратные матрицы имеют обратные, но первое требование к матрице, чтобы иметь обратную матрицу, — это то, что сначала она должна быть квадратной матрицей.
Ознакомьтесь с моим отдельным руководством о том, как найти обратную матрицу 2 × 2.
Я должен подчеркнуть, что для того, чтобы сложить или вычесть две заданные матрицы, они должны иметь одинаковый размер или размер. В противном случае мы заключаем, что сумма (сложение) или разность (вычитание) двух матриц, имеющих разные размеры или размеры, не определена!
Теперь давайте посмотрим на общее правило того, как складывать и вычитать матрицы, размеры или размеры которых совпадают.
Правила сложения и вычитания матриц одинакового размера или измерения
Предположим, что матрицы A и B имеют две строки и два столбца (2 × 2) с некоторыми произвольными элементами или записями…
«Формулы» для сложения и вычитания матриц показаны ниже…
- Добавьте матрицы , добавив их соответствующие записи
- Вычесть матрицы путем вычитания их соответствующих записей
Давайте поработаем над некоторыми проблемами.
Примеры сложения и вычитания матриц
Пример 1 : Выполните указанную операцию для A + C.
Обратите внимание, что матрицы A и C имеют одинаковый «размер» или «размерность», потому что их количество строк и столбцов одинаково. Оба могут быть описаны как матрица 3 x 3 . Это говорит мне о том, что найти их сумму — это нормально.
Добавлю соответствующие записи и упрощу.
Вот как это просто!
Пример 2 : Выполните указанную операцию для B + F.
Обратите внимание, что матрица B имеет размерность 2 × 3 , а матрица F имеет размерность 2 × 2 .
Поскольку количество строк и столбцов не совпадает, сумма матриц B и F не существует или не определена . Я остановлюсь здесь. Это наш ответ, хотите верьте, хотите нет.
Пример 3 : Выполните указанную операцию для E-B.
Последние два примера показали вам, как складывать матрицы. На этот раз мы поговорим о вычитании матриц.Помните, что процесс сложения и вычитания матриц очень похож. Если вы забыли, просмотрите приведенную выше «формулу».
В этом примере нам нужно найти разницу между матрицей E и матрицей B.
Однако кажется, что это невозможно, поскольку они имеют различных размеров или размеров . Матрица E имеет размер 3 × 2, а матрица B — 2 × 3.
Поскольку я не могу вычесть по входам, из-за того, что записи двух матриц не имеют прямого соответствия, я должен утверждать, что НЕ возможно найти их различие.Следовательно, наш ответ: undefined .
Это не вопрос с подвохом. Учителя иногда «добавляют» это в смесь, чтобы проверить, понимаете ли вы концепцию, согласно которой можно складывать или вычитать только матрицы с одинаковыми размерами или размерами. Не расстраивайтесь, я сам попал в эту «ловушку». Надеюсь, теперь, когда вы знаете, вы будете осторожны в следующий раз, когда столкнетесь с такой проблемой.
Пример 4 : Выполните указанную операцию для F-D.
При быстром просмотре я вижу, что можно найти разницу между матрицами F и D, потому что обе имеют одинаковое количество строк и столбцов.Большой!
Для начала я вычту соответствующие записи F и D. Мое единственное предостережение — будьте очень осторожны при вычитании действительных чисел. Обычно здесь возникают общие ошибки. Помните, что два соседних отрицательных знака оказываются положительными.
Неплохо, правда?
Пример 5 : Выполните указанную операцию для C-A.
Две заданные матрицы C и A имеют одинаковые размеры или размеры (обе матрицы 3 × 3). Это позволяет нам выполнять операцию вычитания.
Вычитая по входу, я получил…
Пример 6 : Выполните указанную операцию для (A + C) + (C-A).
Это отличный пример «многоступенчатой» задачи, которая включает в себя сложение и вычитание матриц. Цель состоит в том, чтобы выполнить указанную операцию над каждой круглой скобкой, а затем добавить их вместе.
Чтобы пропустить некоторые шаги, просмотрите, как мы решили для (A + C) в примере 1 и C-A в примере 5.
Пока у нас есть эти частичные ответы…
Итак, последний шаг — сложить их вместе, чтобы получить требуемый ответ.
Как видите, сложение и вычитание матриц очень просто. Я надеюсь, что вы приобрели некоторую уверенность и знания о том, как с этим справиться.
Пример 7 : Выполните указанную операцию для (A + C) + (C-A).
Это та же проблема, что и в примере 6. Но я хочу решить ее немного иначе, чтобы продемонстрировать тот факт, что есть другие способы решения определенной проблемы. Хотя метод, примененный в примере 6, вполне приемлем, этот «альтернативный» подход имеет гораздо больше смысла, поскольку он очень прост.
Поехали…
Если вы рассматриваете выражение (A + C) + (C-A) как , объединяющее похожие или похожие термины, задача типа , то имеет смысл быстро упростить исходную задачу, даже не занимаясь сложением и вычитанием матриц.
Обратите внимание, что я могу объединить C-термины как 2C.
Теперь, члены A должны сокращаться, потому что они имеют противоположные знаки.
Наша исходная задача сводится к 2C, что составляет в два раза больше матрицы C .
Это означает, что я собираюсь умножить каждый элемент матрицы C на 2. На самом деле это тема моего другого урока по алгебре, посвященного скалярному умножению матрицы.
с
, то 2C решается с помощью…
Окончательный ответ, полученный с помощью этого метода, точно такой же, как в примере 6. Легко, правда?
Практика с рабочими листами
Возможно, вас заинтересует:
Скалярное умножение
Умножение матриц
Не знаете о тензорах, измерениях, рангах, порядках, матрицах и векторах? | Ромео Кинцлер | Центр данных с открытым исходным кодом и технологий искусственного интеллекта
Когда дело доходит до терминов _dimensionality_ , _rank_ и _order_ , вы должны различать случай, когда термин описывает вектор или матрицу или тензор.Первые представляют собой математические свойства вектора и матрицы, вторые описывают форму структуры данных под названием _tensor_ .
Позвольте мне объяснить…
Тензор — это не что иное, как математическая структура данных, способ организации данных и набор правил (определенных в линейной алгебре), которые определяют математические операции над ними.
_dimensionality_ , _rank_ или _order_ самого тензора определяет его расширение в пространстве.Следующая таблица иллюстрирует это:
Поскольку основные структуры данных уже рассмотрены, я представляю некоторые возможности и свойства для каждой из них.
Скаляры охватывают одномерное векторное пространство, поскольку они могут однозначно адресовать любую точку в нем. Одномерное векторное пространство также называется _line_ . Это означает, что с бесконечным количеством скалярных значений вы можете адресовать любую точку в строке.
Векторы охватывают векторное пространство любой размерности в зависимости от количества элементов в векторе, поскольку он может однозначно адресовать любую точку в произвольно большом (относительно количества измерений) векторном пространстве.Количество элементов в векторе также называется размерностью или порядком. Это означает, что с бесконечным числом векторов вы можете адресовать любую точку в любом векторном пространстве, независимо от того, сколько измерений она имеет. Двумерное пространство также называют плоскостью. В зависимости от теории, которой вы следуете, наша Вселенная имеет три, четыре (Эйнштейн, пространство-время), пять (Теодор Калуца) или одиннадцать (Эдвард Виттен, теория суперструн) измерений. Но набор данных MNIST, набор данных hello world в нейронных сетях, имеет 784 измерения, поскольку изображения имеют 28 на 28 пикселей.
Это означает, что с бесконечным числом векторов вы можете адресовать любую точку в любом векторном пространстве, независимо от того, сколько измерений она имеет. Двумерное пространство также называют плоскостью. В зависимости от теории, которой вы следуете, наша Вселенная имеет три, четыре (Эйнштейн, пространство-время), пять (Теодор Калуца) или одиннадцать (Эдвард Виттен, теория суперструн) измерений. Но набор данных MNIST, набор данных hello world в нейронных сетях, имеет 784 измерения, поскольку изображения имеют 28 на 28 пикселей.
Матрицы охватывают векторное пространство любой размерности, потому что в зависимости от количества столбцов они могут однозначно адресовать любую точку в произвольном большом (относительно количества измерений) векторном пространстве. Каждая строка в матрице соответствует одной точке в этом пространстве. Другими словами, матрица — это просто набор точек или векторов одинаковой длины. Количество строк говорит вам, сколько точек у вас есть в этом пространстве, а количество столбцов говорит вам, сколько измерений имеет это пространство.
Порядок матрицы — это количество строк (обычно упоминаемых первыми) и столбцов (обычно упоминаемых последними).
Ранг матрицы — это количество линейно независимых компонентов, и его часто путают с порядком матрицы.
Трехмерные тензоры охватывают несколько параллельных векторных пространств одинаковой размерности. В зависимости от количества столбцов он может однозначно адресовать любую точку в произвольно большом (относительно # размеров) векторном пространстве. Каждая строка в трехмерном тензоре соответствует одной точке в этом пространстве, и каждый слой в трехмерном тензоре можно рассматривать как отдельное векторное пространство с тем же количеством измерений и точек.n [/ latex] называется линейно зависимым, если [latex] c_ {1}, \ cdots, c_ {p} [/ latex] не все равны нулю, так что [latex] c_ {1} \ vec {v_ { 1}}, \ cdots, c_ {p} \ vec {v_ {p}} = \ vec {0} [/ latex]. [латекс] c_ {1} \ vec {v_ {1}} + \ cdots + c_ {p} \ vec {v_ {p}} = \ vec {0} [/ latex] называется отношением линейной зависимости между [латексом ] \ vec {v_ {1}}, \ cdots, \ vec {v_ {p}} [/ latex].
Пример 1 : Определите, если набор [latex] \ begin {Bmatrix} \ vec {v_ {1}}, \ vec {v_ {2}}, \ vec {v_ {3}} \ end {Bmatrix} [ / латекс] линейно независим.Если возможно, найдите отношение линейной зависимости между [latex] \ vec {v_ {1}}, \ vec {v_ {2}}, \ vec {v_ {3}} [/ latex]. [латекс] \ vec {v_ {1}} = \ begin {bmatrix} -1 \\ 2 \\ 3 \ end {bmatrix} [/ latex], [латекс] \ vec {v_ {2}} = \ begin { bmatrix} 4 \\ — 1 \\ 9 \ end {bmatrix} [/ latex] и [latex] \ vec {v_ {3}} = \ begin {bmatrix} 2 \\ — 4 \\ — 6 \ end { bmatrix} [/ латекс].
Упражнение 1 : Определите, если набор [latex] \ begin {Bmatrix} \ vec {v_ {1}}, \ vec {v_ {2}}, \ vec {v_ {3}} \ end {Bmatrix} [ / латекс] линейно независим.Если возможно, найдите отношение линейной зависимости между [latex] \ vec {v_ {1}}, \ vec {v_ {2}}, \ vec {v_ {3}} [/ latex]. [латекс] \ vec {v_ {1}} = \ begin {bmatrix} -2 \\ 2 \\ — 3 \ end {bmatrix} [/ latex], [латекс] \ vec {v_ {2}} = \ begin {bmatrix} 6 \\ — 1 \\ 4 \ end {bmatrix} [/ latex] и [latex] \ vec {v_ {3}} = \ begin {bmatrix} 4 \\ — 4 \\ 6 \ end { bmatrix} [/ латекс].
Примечание: 1. Для матрицы [латекс] A = \ begin {bmatrix} \ vec {v_ {1}}, \ cdots, \ vec {v_ {p}} \ end {bmatrix} [/ latex] с [ latex] p [/ latex] столбцы, матричное уравнение [latex] A \ vec {x} = \ vec {0} [/ latex] можно записать как [latex] x_ {1} \ vec {v_ {1}} + \ cdots + x_ {p} \ vec {v_ {p}} = \ vec {0} [/ latex].Тогда каждое отношение линейной зависимости между столбцами [latex] A [/ latex] соответствует нетривиальному решению [latex] A \ vec {x} = \ vec {0} [/ latex]. Следовательно, столбцы матрицы [latex] A [/ latex] линейно независимы тогда и только тогда, когда уравнение [latex] A \ vec {x} = \ vec {0} [/ latex] имеет только тривиальное решение.
2. Набор только с одним вектором линейно независим тогда и только тогда, когда он не является нулевым вектором. Нулевой вектор линейно зависим.
Нулевой вектор линейно зависим.
3.Набор с двумя векторами линейно независим тогда и только тогда, когда они не кратны друг другу.
Пример 2 : Покажите, что набор столбцов [latex] A [/ latex] является линейно независимым набором. [латекс] A = \ begin {bmatrix} 2 & 0 & 1 \\ 1 & -1 & 0 \\ — 1 & 2 & 1 \ end {bmatrix} [/ latex].
Упражнение 2 : Покажите, что набор столбцов [latex] A [/ latex] является линейно независимым набором. [латекс] A = \ begin {bmatrix} 1 & 2 & 1 \\ 0 & -1 & 2 \\ — 1 & -2 & 0 \ end {bmatrix} [/ latex].n [/ latex] содержит нулевой вектор, тогда он линейно зависим.
Пример 3 : Используйте проверку, чтобы решить, является ли набор векторов линейно независимым. Изложите рассуждение.
(a) [латекс] \ begin {bmatrix} 2 \\ 1 \\ — 1 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} -4 \\ — 2 \\ 2 \ end { bmatrix} [/ латекс].
(b) [латекс] \ begin {bmatrix} 2 \\ 1 \\ — 1 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} 3 \\ 4 \\ 5 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} 0 \\ 0 \\ 0 \ end {bmatrix} [/ latex].
(c) [латекс] \ begin {bmatrix} 2 \\ 1 \\ — 1 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} 3 \\ 4 \\ 5 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} -2 \\ 6 \\ — 7 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} 0 \\ 2 \\ 1 \ end { bmatrix} [/ латекс].
Упражнение 3 : Используйте проверку, чтобы решить, является ли набор векторов линейно независимым. Изложите рассуждение.
(a) [латекс] \ begin {bmatrix} 2 \\ 1 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} -4 \\ — 2 \ end {bmatrix} [/ latex], [латекс] \ begin {bmatrix} 4 \\ 3 \ end {bmatrix} [/ latex].
(b) [латекс] \ begin {bmatrix} 2 \\ 1 \\ 0 \\ — 1 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} 3 \\ 2 \\ 1 \\ 5 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} 0 \\ 0 \\ 0 \\ 0 \ end {bmatrix} [/ latex], [latex] \ begin {bmatrix} 2 \\ 1 \\ — 1 \\ 3 \ end {bmatrix} [/ латекс]. n [/ latex], то любой линейно независимый набор ровно элементы [latex] p [/ latex] в [latex] H [/ latex] автоматически являются основой для [latex] H [/ latex].n [/ латекс]:
n [/ latex], то любой линейно независимый набор ровно элементы [latex] p [/ latex] в [latex] H [/ latex] автоматически являются основой для [latex] H [/ latex].n [/ латекс]:
[латекс] U = \ left \ {\ begin {bmatrix} a \\ a + b \\ a-2c \\ c \ end {bmatrix} | a, b, c \ text {in} \ mathbb {R} \ right \} [/ латекс],
[латекс] V = \ left \ {\ begin {bmatrix} a \\ b \\ c \\ d \ end {bmatrix} | a — 2b + c + d = 0 \ text {in} \ mathbb {R} \ right \} [/ латекс].
GroupWork 1: Отметьте каждое утверждение как истинное или ложное. Обоснуйте каждый ответ.
а. Если [latex] B [/ latex] является эшелонированной формой матрицы [latex] A [/ latex], то опорные столбцы [latex] B [/ latex] образуют основу для Col [latex] A [/ latex ].
г. Операции со строками не влияют на отношения линейной зависимости между
столбцами матрицы.
г. Столбцы матрицы [latex] A [/ latex] линейно независимы, если уравнение [latex] A \ vec {x} = \ vec {0} [/ latex] имеет только тривиальное решение.
г. Столбцы любой матрицы [latex] 4 \ times 5 [/ latex] линейно зависимы.
e. Если [латекс] \ vec {u} [/ latex] и [latex] \ vec {v} [/ latex] линейно независимы и если [latex] \ vec {w} [/ latex] находится в Span [латексе] \ left \ {\ vec {u}, \ vec {v} \ right \} [/ latex], затем [latex] \ left \ {\ vec {u}, \ vec {v}, \ vec {w} \ right \ } [/ latex] линейно зависим.n [/ latex] является линейно зависимым, тогда он содержит более [latex] n [/ latex] векторов.
GroupWork 2: Опишите возможную эшелонированную форму матрицы.
(a) [latex] A [/ latex] — это матрица [latex] 2 \ times 2 [/ latex] с линейно независимыми столбцами.
(b) [латекс] A [/ latex] представляет собой матрицу [латекс] 4 \ times 2 [/ latex], так что первый столбец кратен второму столбцу.
GroupWork 3: В каждом случае покажите, что утверждение истинно, или приведите пример, показывающий, что оно ложно.
а. Если [латекс] \ left \ {\ vec {u}, \ vec {v} \ right \} [/ latex] независим, тогда [латекс] \ left \ {\ vec {u}, \ vec {v}, \ vec {u} + \ vec {v} \ right \} [/ latex] не зависит.
г. Если [латекс] \ left \ {\ vec {u}, \ vec {v}, \ vec {w} \ right \} [/ latex] независим, то [latex] \ left \ {\ vec {u}, \ vec {v} \ right \} [/ latex] не зависит.
г. Если [латекс] \ left \ {\ vec {u}, \ vec {v} \ right \} [/ latex] зависит, то [латекс] \ left \ {\ vec {u}, \ vec {v}, \ vec {w} \ right \} [/ latex] зависит от любого [латекса] \ vec {w} [/ latex].4 [/ латекс]? Почему?
Умножение матрицУмножение матриц
Рассмотрим произведение матрицы 2 × 3 и матрицы 3 × 4. Умножение определяется, потому что внутренние размеры (3) одинаковы. Продукт будет — матрица 2 × 4, внешние размеры.
Так как в первой матрице три столбца и три строки во второй матрица (внутренние размеры должны быть одинаковыми), каждый элемент в продукте будет сумма трех продукты.
Ряд 1, Столб 1
Чтобы найти элемент в строке 1, столбце 1 продукта, мы возьмем строку 1 из первой матрицы и столбец 1 из второй матрицы. Мы объединяем эти значения в пары, умножаем пары значений, а затем добавляем к прибыть на 25.
R 1 : 1-2 3
× С 1 : 1-3 6
---------------
1 +6 +18 = 25 Ряд 2, столбец 3
Чтобы найти элемент в строке 2, столбце 3 продукта, возьмем строку 2 из первой матрицы и столбец 3 из второй матрицы.Мы объединяем эти значения вместе, умножьте пары значений, а затем добавьте к прибыть на 53.
R 2 : 4 5 -2
× C 3 : 4 7-1
---------------
16 +35 +2 = 53 Понимание происхождения каждого числа в продукте полезно, когда
вам нужно только конкретное значение. Вам не нужно полностью размножаться, если вы
нужны только определенные элементы. Просто возьмите строку из первой матрицы и
столбец из второй матрицы.
Процесс может быть завершен для остальных элементов в матрице.
| Колонка 1 | Колонка 2 | Колонка 3 | Колонка 4 | ||
|---|---|---|---|---|---|
| значений | [1, -3, 6] | [-8, 6, 5] | [4, 7, -1] | [-3, 2, 4] | |
| Ряд 1 | [1, -2, 3] | 1 (1) — 2 (-3) + 3 (6) = 1 + 6 + 18 = 25 | 1 (-8) -2 (6) + 3 (5) = -8 — 12 + 15 = -5 | 1 (4) -2 (7) +3 (-1) = 4-14-3 = -13 | 1 (-3) -2 (2) + 3 (4) = -3-4 + 12 = 5 |
| Ряд 2 | [4, 5, -2] | 4 (1) + 5 (-3) -2 (6) = 4-15-12 = -23 | 4 (-8) + 5 (6) — 2 (5) = -32 + 30-10 = -12 | 4 (4) + 5 (7) -2 (-1) = 16 + 35 + 2 = 53 | 4 (-3) + 5 (2) -2 (4) = -12 + 10-8 = -10 |
Итак, конечный продукт —
| 25 | -5 | -13 | 5 | ||
| -23 | -12 | 53 | -10 |
Умножение матриц не коммутативно
Обратите внимание, что умножение не определяется другим способом.Нельзя размножаться 3×4 и матрица 2×3 вместе, потому что внутренние размеры не совпадают.
Этот товар не определен.
Матрицы— Операции и инверсии
Как умножить с помощью матриц?
Есть два вида умножения с матрицами: скалярное
умножение и умножение
матрицы .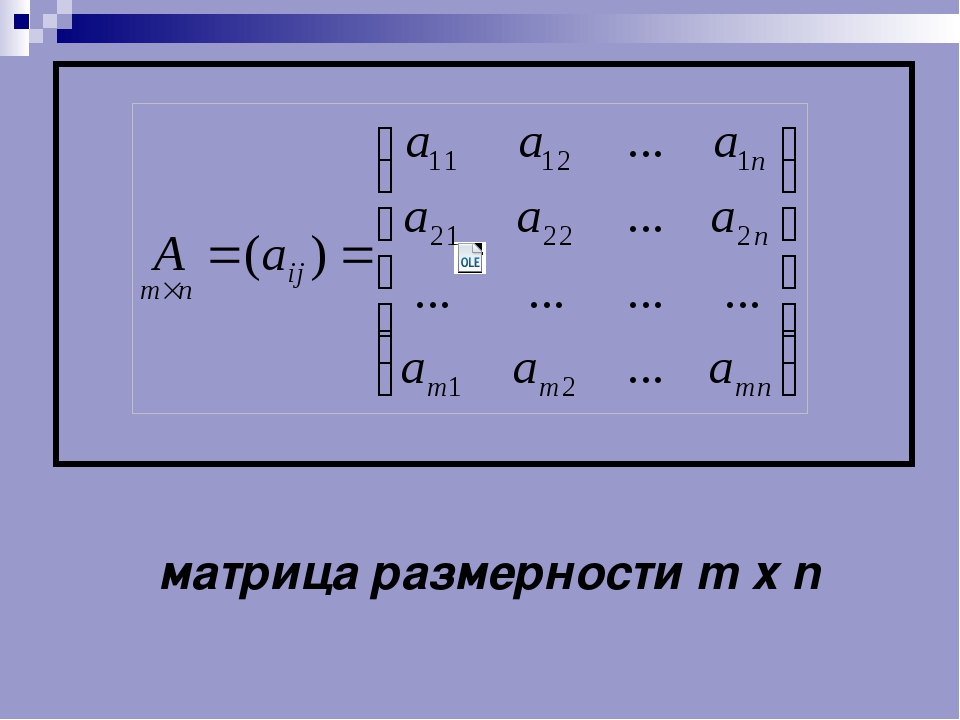
 77841574, 0.39654203, 0.38188665, 0.26704305],
[ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
[ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])
77841574, 0.39654203, 0.38188665, 0.26704305],
[ 0.27519705, 0.78115866, 0.96019214, 0.59328414],
[ 0.52008642, 0.10862692, 0.41894881, 0.73581471]])