Золотое сечение и числа Фибоначчи
Законы природы и законы Жизни до сих пор не разгаданы. И каждый новый взгляд на обычные вещи отображается новым открытием или новыми изобретениями. Жизнь интересная штука! И каждый раз узнаешь о чем-то новом.
Для меня было большим открытием узнать о золотом сечение и числах Фибоначчи. Я до сих пор под впечатлением. И спешу рассказать Вам об этом обычном (для мира) и уникальном (для человечества) явлении.
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи).
Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами.
В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 … и т.д.
Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 … и т.д.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … и т.д.
Набор этих чисел известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф.
Последовательность Фибоначчи — это числовой ряд, в котором каждый последующий член представляет собой сумму двух предыдущих:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д.
- каждое последующее число в числовом ряду приблизительно в 1.618 раз больше предыдущего, а каждое предыдущее составляет приблизительно 0.618 от следующего.
- Отношение через одно число составляет 0.382, а обратное ему число = 2.618. За исключением нескольких первых чисел последовательности.
Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.
Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.
Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы.
Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.
Понравилась статья? Расскажи о ней своим друзьям в социальных сетях, жми соответствующую кнопку ниже!
Tags: Законы Успеха, Золотое сечение, Колесо Жизненного Баланса, Правила Жизни, ряд Фибоначчи
Числа Фибоначчи и золотое сечение. А при чем здесь стоматология? |
Эстетическое направление в стоматологии развивается стремительно.
Но, как и в любой другой сфере, так или иначе связанной с красотой, здесь тоже есть принципы, над которыми не властно время. Одним из таких принципов является принцип золотого сечения, описанный в XIII веке средневековым математиком Леонардо Фибоначчи. Хотя поначалу этот концепт окружал некий ореол мистицизма, сейчас ни у кого не возникает сомнений по поводу релевантности золотого сечения.
Задолго до Фибоначчи древние греки пользовались этим принципом, чтобы создавать произведения искусства. Сам Леонардо Да Винчи прибегал к золотой пропорции практически во всех своих творениях. Этим же принципом руководствуются и современные автомобильные дизайнеры.
Ряд ФибоначчиПоследовательность Фибоначчи встречается в природе практически на каждом шагу – в количестве лепестков розы или кроликов, родившихся за год. Кстати, последний пример особенно волновал Фибоначчи в 1202 году.
Ряд Фибоначчи представляет собой числовую последовательность, первые значения которого равны 0 или 1, а каждое последующее равно сумме двух предыдущих.
Выглядит это следующим образом: 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 и т.д.. В конечном счете получается последовательность: 1, 1, 2, 3, 5, 8, 13 …
Золотое сечениеЕсли поделить одно число из последовательности на предшествующее ему, то получится значение, близкое к 1,618. С развитием последовательности частное, которое еще называют числом Фи, становится все более точным. А его инверсия – 0,618 или число фи – как раз считается золотым сечением.
Числа Фибоначчи лежат в основе золотого сечения (1:1,618) и, как следствие, золотой спирали и золотого прямоугольника. Кредитная карта представляет собой идеальный пример золотого прямоугольника. Ее измерения равны 53 мм и 86 мм. Умножив 53 на число Фи или 1,618, получаем 86.
Лучше всего представить себе золотую спираль на примере раковины моллюска наутилуса. Золотая спираль основывается на квадратах из числа последовательности Фибоначчи, начиная с 1×1.
Золотое сечение используется при определении размера зуба.
Средняя ширина центрального резца составляет примерно 8 мм. Ширина двух центральных резцов будет равняться 16 мм. Если мы хотим определить идеальную эстетическую длину этих самых резцов, мы можем поделить 16 на 1,618 и получится 9,89 мм. Такие расчеты помогают при восстановлении зубов.
Приведем еще один пример. Ширина центральных резцов является хорошей отправной точкой в расчетах. Поэтому допустим, что 8,5 мм является идеальной шириной для конкретного пациента. Ширина обоих центральных резцов составляет 17, а идеальная эстетическая длина — 10,5 мм (17 / 1,618 = 10,5). Если мы разделим ширину этого центрального резца на число Фи, у нас получится результат, с помощью которого можно вернуть идеальную эстетическую визуальную ширину зуба позади него (боковой резец). Следовательно, 8,5 мм / 1,618 = 5,3 мм, и в этом случае это идеальная визуальная ширина бокового резца.
Стоит учитывать, что речь идет именно о визуальной, а не фактической ширине бокового резца. Можно посчитать все еще раз, определяя идеальную ширину клыка: 5,3 мм / 1,618 = 3,3 мм, первого премоляра позади него: 3,3 мм / 1,618 = 2,0 мм, второго премоляра: 2,0 мм / 1,618 = 1,2 мм и т.д..
Таким образом у нас вырисовывается вполне конкретный план реставрации.
Использование золотого сечения — это всего лишь инструмент для создания идеальной эстетической улыбки. Оно может предоставить стоматологу информацию, которая поможет начать разработку новой улыбки пациента. Золотое сечение не является единственным залогом успеха, поскольку есть много других факторов, которые необходимо учитывать.
Поделиться ссылкой:
The following two tabs change content below.Автор и редактор блога Стомдевайс.
Специализируется на стоматологии, медицине и маркетинге.
В 2018 году стажировалась в отделе локализации Google.
В 2017 и 2018 году стала призером Международной научной конференции молодых ученых в МГУ.
С 2015 года профессионально занимается переводами с английского языка.
Что такое числа Фибоначчи, золотое сечение? ⋆ FutureNow
Последовательность Фибоначчи – одна из самых известных формул математики. Так, что такое числа Фибоначчи, золотое сечение и какая их интересная стория?
Каждое число в последовательности Фибоначчи – это сумма двух чисел, предшествующих ему.
Итак, последовательность выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т. Математическое уравнение, описывающее число Фибоначчи: Xn + 2 = Xn + 1 + Xn
Фибоначчи числа иногда называют “секретным кодом природы” и “общем правилом природы”. Говорят, что данная последовательность руководит размерами всего сущего, в том числе обьясняет Великую пирамиду в Гизе, так и многие вещи, с которыми мы сталкиваемся каждый день.
Числа Фибоначчи: богатая историяМногие источники утверждают, что ее впервые обнаружил или “изобрел” Леонардо Фибоначчи.
Итальянский математик, родился около 1170 года нашей эры и первоначально был известен как Леонардо из Пизы. Лишь в 19 веке историки придумали прозвище Фибоначчи, чтобы отличить математика от другого известного Пизарського Леонардо.
Но Леонардо из Пизы на самом деле не изобрел последовательность. Ее впервые упоминают древние санскритские тексты, в которых использовалась индуистско-арабская система числения, еще много веков до Леонардо Пизы.
Однако в 1202 Леонардо из Пизы опубликовал большой том “Liber Abaci,” книгу по математике “о том, как производить вычисления”. “Liber Abaci”, написанная для торговцев, где изложена индуистско-арабский арифметика, которая является полезной для отслеживания прибыли, убытков, остатков по кредитам и тому подобное.
ЧТО ТАКОЕ ШАРОВАЯ МОЛНИЯ: СУЩЕСТВУЕТ ЛИ ОНА?
В книге Леонардо из Пизы вводит последовательность с задачей о кроликах.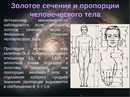
Проблема заключается в следующем: начнем с самца и самки кролика. Через месяц они созревают и дают помет в результате которого мы имеем еще самца и самку кролика. Через месяц эти кролики размножаются и получается – вы догадались – еще один самец и самка, которые также могут спариваться через месяц. Через год сколько бы у вас было кроликов? Ответ, 144, спрятан в формуле, которая сейчас известна как последовательность Фибоначчи.
“Liber Abaci” впервые представила эту последовательность западному миру. Но после нескольких скудных абзацев о разведении кроликов Леонардо из Пизы больше никогда не вспоминал ее.
На самом деле эти числа Фибоначчи были забыты до 19 века, когда математики подробнее изучили математические свойства последовательности. В 1877 году французский математик Эдуард Лукас официально назвал задачу о кроликах “последовательностью Фибоначчи”.
Числа Фибоначчи и золотое сечениеМы узнали что такое числа Фибоначчи, но какое же значение имеет последовательность Фибоначчи?
Кроме как учебный инструмент, она проявляется во многих случаях в природе. Однако, это не какой-то секретный код, который руководит архитектурой Вселенной.
Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как “золотое сечение”. Проще говоря, отношение чисел в последовательности, поскольку последовательность идет к бесконечности, приближается к золотому сечению, который составляет +1,6180339887498948482 … Оттуда математики могут вычислить то, что называется золотой спиралью, или логарифмической спирали, коэффициент роста которой равен золотому сечению.
Золотое сечение объясняет рост некоторых растений. Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Но есть также растения, которые не соблюдают этого правила.
Мистификации и выдумкиКогда люди начинают связывать человеческое тело, искусство и архитектуру, много вымышленных теорий и мистификаций ссылаются на последовательность Фибоначчи.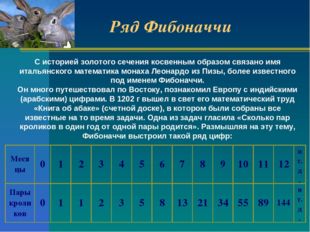
“Понадобится большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, многие из которой – это просто повторение одних и тех же фантазий разных авторов”, – написал Джордж Марковский, математик из университета Мэн в 1992 году.
Значительная часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Зейзинга. Он утверждал, что пропорции человеческого тела основана на золотом сечении.
Золотое соотношение проросло в “золотые прямоугольники”, “золотые треугольники” и всевозможные теории об этих знаковых размерах.
С тех пор люди говорят, что золотое соотношение или золотое сечение можно найти в размерах Пирамиды в Гизе, Парфеноне, “Витрувийським человеке” Леонардо да Винчи и ренессансных сооружениях.
Под сомнение можно поставить и беспрекословное утверждение о том, что золотое сечение является “однозначно приятным” для человеческого глаза – на чем часто настаивают фотографы.
Часто все эти утверждения, когда их проверяют, являются ошибочными. Люди часто выдают желаемое за действительное.
Источник: www.livescience.com/
Фибоначчи повсюду!. Числа Фибоначчи названы в честь… | by Сергей Базанов | Paradox Review
Числа Фибоначчи и золотое сечение
Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».
Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.
Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.
Числа Фибоначчи и золотое сечение окружают нас повсюду. Вот примеры | Хакнем Школа
Дэн Браун «Код да Винчи»#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Недавно, читая роман Дэна Брауна «Код да Винчи», я по-новому посмотрела на известные со школы: последовательность чисел Фибоначчи, «золотое сечение» и число Фи. Герой романа использует в качестве кода несколько чисел этого ряда.
Своими новыми для себя открытиями я решила поделиться с нашими читателями.
Удивительную последовательность чисел открыл итальянский математик Леонардо Пизанский, более известный под именем Фибоначчи (родился около 1170 — умер после 1228).
Числа, образующие последовательность:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … называются «числами Фибоначчи», а сама последовательность — последовательностью Фибоначчи. Что же в них такого удивительного?
Числовая последовательность Фибоначчи в задачке с размножением кроликов1) В этой последовательности первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число получается из суммы двух предыдущих чисел: 1 = 0 +1, 2 = 1 + 1, 3 = 1 +2, 5 = 2 + 3, 8 = 3 +5, и т. д.
2) Ещё одна особенность в том, что при делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то — превосходящая, то — не достигающая его. После 13-ого числа этот результат деления становится постоянным до бесконечности ряда.
Именно это постоянное число деления в средние века было названо Божественной пропорцией, а в наши дни именуется, как золотое сечение. В алгебре это число обозначается греческой буквой фи (φ).
Итак, Золотая пропорция = 1 : 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618 и т.д., можете проверить сами…
Но самое интересное, что меня поразило, это то, что золотая пропорция есть как в нашем теле, так и в природе.
Тело человека и золотое сечение«Витрувиа́нский человек» — изображение, созданное Леонардо да ВинчиОказывается, художники, учёные, модельеры и дизайнеры делают свои расчёты, чертежи или наброски, исходя из соотношения золотого сечения, так как пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению.
Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенным.
Несколько основных золотых пропорций нашего тела:
· расстояние от кончиков пальцев до запястья равно 1:1,618;
· расстояние от уровня плеча до макушки головы и размера головы равно 1:1,618;
· расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1,618;
· расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1,618 и др.
Формулу золотого сечения можно найти в других частях тела человека: и в руках человека, и ушах, и в строении лёгких и даже в строении молекулы ДНК (если интересно, можно найти информацию самостоятельно).
Золотой прямоугольникЗолотой прямоугольникВ геометрии есть такой прямоугольник, который называют золотым прямоугольником, его длинные стороны соотносятся с короткими сторонами в соотношении 1,168:1.
Он обладает удивительными свойствами — отрезав от золотого прямоугольника квадрат, строна которого равна меньшей стороны прямоугольника, мы снова получим золотой прямоугольник, но меньшего размера. Продолжая отрезать квадраты, мы будем получать всё меньшие и меньшие золотые прямоугольники.
Причём, располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, раковинах улиток).
ПРИРОДАИдеальную пропорцию создала сама природаВ природе, лежащее в основе строения спирали, правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях:
- числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи;
- расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи;
- семена в центре подсолнуха организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки;
- у большинства улиток, которые обладают раковинами, раковина растёт в форме логарифмической спирали.
Оказывается, числа Фибоначчи повсюду вокруг нас!
#хакнем_математика 👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳
Автор: #ирина_чудневцева 41 год, город Ярославль, мама 16-летнего подростка.
Золотое сечение. Числа Фибоначчи в техническом анализе Текст научной статьи по специальности «Математика»
УДК 81:72.
013 К.Ю. Баклина
Омский государственный технический университет, г. Омск
ЗОЛОТОЕ СЕЧЕНИЕ.
ЧИСЛА ФИБОНАЧЧИ В ТЕХНИЧЕСКОМ АНАЛИЗЕ
Предмет общей теории терминологии составляет изучение формирования и употребления специальных слов, с помощью которых передаются накопленные человечеством знания, а так же отражаются взаимоотношения человека и общества. Термины отрасли, будь то наука или производство, формируют свои системы, которые определяются понятийными связями профессионального знания при стремлении выразить эти связи языковыми средствами. Тем самым, язык оказывается структурным элементом научного знания. Чем наука «научнее», тем больше вес языка в ее структуре. Язык входит в науку прежде всего терминами. Обратимся к терминам «Золотое сечение» и «Числа Фибоначчи».
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление), термин относящийся к древней проблеме, решенной пифагорейцами, о делении отрезка на части в таком соотношении, при котором большая часть относится к меньшей, как сумма к большей. Принцип золотого сечения — высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Золотым сечением интересовались по разным причинам. Исходя из золотого сечения, Платон пришел к представлению об основах знания; Аристотель извлек из золотого сечения этические аналогии, а некоторые средневековые мыслители называли его божественной пропорцией.
Ныне золотое сечение привлекает внимание главным образом в связи с определением гармонических пропорций в архитектуре и других видах искусств.
Термин «золотое сечение» был введен Леонардо да Винчи, который использовал золотое сечение как пропорции «идеального человеческого тела». Американский математик Марк Барр, предложил называть отношение двух отрезков, образующих золотое сечение,
числом . Буква (фи) — первая буква в имени великого Фидия, который, по преданию, часто использовал золотое сечение в своих скульптурах.
Чему же равно ? PHI — число, по всеобщему мнению, признано самым красивым во вселенной. Пирамида Хеопса, самая известная из египетских пирамид, знаменитый греческий храм Парфенон, большинство греческих скульптурных памятников, «Джоконда» Леонардо да Винчи, картины Рафаэля, Шишкина, этюды Шопена, музыка Бетховена, Чайковского, стихи Пушкина и Шота Руставели — вот далеко не полный перечень выдающихся произведений искусства, наполненных чудесной гармонией, основанной на Золотом Сечении. Число PHI, равное 1.618, получено из последовательности Фибоначчи. Сам ряд последовательности выглядит как вид: 1-1-2-3-5-8-13-21-34-55-89-144-…. Здесь каждый следующий элемент является сложенной суммой двух предыдущих чисел. Отношение любого числа из последовательности к предыдущему, стремится всегда к значению 1.618. Существует еще одна закономерность — любое число ряда соотносится к следующему примерно как 0.618. Это и есть всем известное «золотое сечение» или «божественная пропорция».
Многие математики, жившие в средние века и в эпоху Возрождения, были настолько
увлечены исследованием необычайных свойств числа , что это походило на легкое помешательство.
В 1855 г.
немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. Адольф Цейзинг доказывает, что из всех пропорций именно золотое сечение дает наибольший художественный эф-
фект и доставляет наибольшее удовольствие при восприятии.
Так же пример использования золотого сечения для получения гармоничного фотоснимка. Он основан на подмеченном психологами и искусствоведами правиле — расположении основных компонентов кадра в особых точках — зрительных центрах. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.
7
8
Человек всегда акцентирует свое внимание на этих точках, независимо от формата кадра или картины.
В настоящее время числа Фибоначчи усиленно изучаются бизнесменами и экономистами. Разбираясь с числами Фибоначчи и волнами Эллиота, вы можете разбогатеть, играя на бирже ценных бумаг.
Ральф Нельсон Эллиотт (американский финансист) еще в 30-е годы высказал свою мысль использования последовательности Фибоначчи при прогнозировании цены, то есть техническом анализе. С тех пор конкретная польза применения этой идеи практически во всех методах технического анализа не вызывает сомнения.
Этот шанс предсказать движения цен побуждает аналитиков трудиться денно и ношно. Эллиоттписал: «любой человеческой деятельности присущи три отличительных особенности: форма, время и отношение, — и все они подчиняются суммационной последовательности Фибоначчи».
Один из простейших способов применения чисел Фибоначчи на практике — определение отрезков времени, через которое произойдет то или иное событие, например, изменение тренда.
Аналитик отсчитывает определенное количество фибоначчиевских дней или недель (13, 21, 34, 55 и т.д.) от предыдущего сходного события.
Числа Фибоначчи имеют широкое применение при определении длительности периода в Теории Циклов. За основу каждого доминантного цикла берется определенное количество дней, недель, месяцев, связанное с числами Фибоначчи.
К сожалению, волны Эллиота очень хорошо просматриваются на «старом» рынке и туманно видны для будущего. В связи с этим практическое использование волновой теории Эллиота зачастую проблематично и требует специальных знаний. Если вы не обладаете последними, то можете воспользоваться прогнозами аналитических фирм, которые опираются исключительно на теории Эллиота.
Необходимо отметить также тот факт, что свою теорию Эллиот вывел на основе анализа фондового рынка. Для валютного рынка волны Эллиота могут, очевидно, иметь как прямое их сопоставление, так и обратное. Это будет выражаться в том, что 8 волн (5 бычьих и 3 медвежьих), характерных для анализа фондового рынка, на валютном рынке могут иметь свою противоположность — 5 медвежьих и 3 бычьих волны. Связано это с тем, что любая из котировок валют имеет как прямое свое обозначение, так и обратное.
Библиографический список
1. Дональд Кнут, Рональд Грэхем, ОренПаташник- Конкретнаяматематика. Основание-информатики = Concrete Mathematics. A Foundationfor Computer Science. — М.:Мир; Бином. Лабораториязнаний, 2006.- 303с.
2. Knuth, D. E., Fibonacci multiplication, Appl. Math. Lett.1, Zeckendorf, E., 1988.- 57-60с.
3. Рудаков, А. Н. Числа Фибоначчи и простота числа 2127/ А. Н. Рудаков // Математическое просвещение, третья серия.
— 2000. — Т. 4.
4 Фишер, Р.Новые методы торговли по Фибоначчи / Р. Фишер.- М.:»ИК «Аналитика», 2002.- 384 с.
Число Фибоначчи. Почему оно так популярно в природе?
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Последовательность Фибоначчи
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Читайте также: Найдено самое длинное простое число Мерсенна, состоящее из 22 миллионов цифр
Где используется число Фибоначчи
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.
Проявление золотого сечения в природе
Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.
Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому.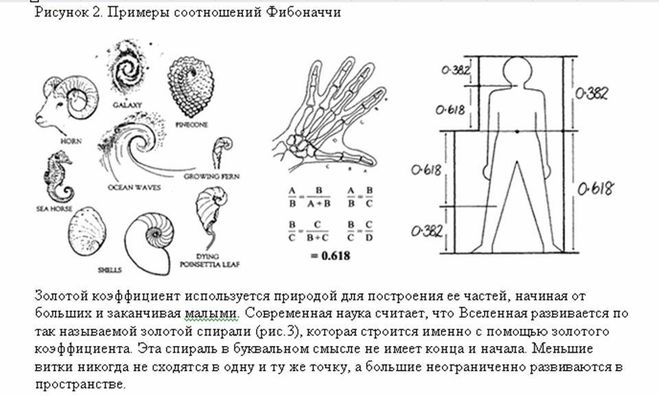
Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.
Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением
Что такое золотое сечение
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.
Так выглядит «золотое сечение»
Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты
Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.
Фибоначчи и золотое сечение
Существует уникальное соотношение, которое можно использовать для описания пропорций всего, от мельчайших строительных блоков природы, таких как атомы, до самых сложных структур во Вселенной, таких как невообразимо большие небесные тела. Природа полагается на эту врожденную пропорцию для поддержания баланса, но финансовые рынки, похоже, также соответствуют этому «золотому сечению». Здесь мы рассмотрим некоторые инструменты технического анализа, которые были разработаны для использования этого паттерна.
Математика
Математики, ученые и естествоиспытатели знали о золотом сечении на протяжении веков. Оно получено из последовательности Фибоначчи, названной в честь ее итальянского основателя Леонардо Фибоначчи (чье рождение предполагается примерно в 1175 году нашей эры, а смерть — примерно в 1250 году нашей эры).
В этой последовательности каждое число представляет собой просто сумму двух предыдущих чисел ( 1, 1, 2, 3, 5, 8, 13 и т. Д.).
Ключевые выводы
- Золотое сечение описывает предсказуемые узоры на всем, от атомов до огромных звезд на небе.
- Соотношение получено из так называемой последовательности Фибоначчи, названной в честь ее итальянского основателя Леонардо Фибоначчи.
- Природа использует это соотношение для поддержания баланса, и финансовые рынки, похоже, тоже.
- Последовательность Фибоначчи может применяться к финансам с использованием четырех основных методов: ретрейсментов, дуг, вееров и часовых поясов.
Но эта последовательность не так уж и важна; скорее, существенная часть — это частное соседнего числа, которое имеет удивительную пропорцию, примерно 1.618 или его обратное 0,618. Эта пропорция известна под многими именами: золотое сечение, золотая середина, PHI и божественная пропорция, среди прочих. Итак, почему это число так важно? Что ж, почти все имеет размерные свойства, которые соответствуют соотношению 1,618, так что кажется, что оно имеет фундаментальную функцию для строительных блоков природы.
Докажи это
Не верите? Возьмем, к примеру, пчел. Если вы разделите пчел-самок на пчел-самцов в любом конкретном улье, вы получите 1.618. У подсолнухов, у которых есть противоположные спирали семян, соотношение диаметров каждого вращения составляет 1,618. Это же соотношение можно увидеть во взаимоотношениях между различными компонентами в природе.
Вы все еще не можете в это поверить? Вам нужно что-то, что легко измерить? Попробуйте измерить расстояние от плеча до кончиков пальцев, а затем разделите это число на длину от локтя до кончиков пальцев. Или попробуйте измерить расстояние от головы до ног и разделить его на длину от пупка до ступней.Результаты такие же? Где-то в районе 1.618? Казалось бы, золотое сечение неизбежно.
Но означает ли это, что это работает в сфере финансов? На самом деле, финансовые рынки имеют ту же математическую основу, что и эти природные явления.
Ниже мы рассмотрим некоторые способы применения золотого сечения к финансам и покажем несколько диаграмм в качестве доказательства.
Исследования Фибоначчи и финансы
При использовании в техническом анализе золотое сечение обычно переводится в три процента: 38.2%, 50% и 61,8%. Однако при необходимости можно использовать больше кратных, например 23,6%, 161,8%, 423% и т. Д. Между тем, есть четыре способа применения последовательности Фибоначчи к графикам: ретрейсменты, дуги, вееры и часовые пояса. Однако не все могут быть доступны в зависимости от используемого графического приложения.
1. Уровни коррекции Фибоначчи
При коррекции Фибоначчи горизонтальные линии используются для обозначения областей поддержки или сопротивления. Уровни рассчитываются с использованием точек максимума и минимума графика.Затем рисуются пять линий: первая — 100% (максимум на графике), вторая — 61,8%, третья — 50%, четвертая — 38,2% и последняя — 0% (минимум на графике). ). После значительного движения цены вверх или вниз новые уровни поддержки и сопротивления часто оказываются на этих линиях или около них.
Изображение Сабрины Цзян © Investopedia 20202. Дуги Фибоначчи
Поиск максимума и минимума графика — это первый шаг к составлению дуг Фибоначчи. Затем движением, похожим на компас, рисуем три изогнутые линии в точке 38.2%, 50% и 61,8% от желаемой точки. Эти линии предполагают уровни поддержки и сопротивления, а также торговые диапазоны.
Изображение Сабрины Цзян © Investopedia 20203. Веера Фибоначчи
Веера Фибоначчи состоят из диагональных линий. После определения максимума и минимума графика через крайнюю правую точку проводится невидимая горизонтальная линия. Затем эта невидимая линия делится на 38,2%, 50% и 61,8%, и линии проводятся от крайней левой точки через каждую из этих точек.Эти линии указывают на области поддержки и сопротивления.
Изображение Сабрины Цзян © Investopedia 20204.
Часовые пояса ФибоначчиВ отличие от других методов Фибоначчи, часовые пояса представляют собой серию вертикальных линий. Они состоят из разделения диаграммы на сегменты с вертикальными линиями, разнесенными друг от друга с шагом, соответствующим последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13 и т. Д.). Каждая линия указывает время, в которое можно ожидать значительного движения цены.
Изображение Сабрины Цзян © Investopedia 2020Золотое сечение можно применить ко всему: от природы до анатомии человека и финансов.
Итог
Исследования Фибоначчи не предназначены для предоставления основных указаний для определения времени входа и выхода из позиции; однако числа полезны для оценки областей поддержки и сопротивления. Многие люди используют комбинации исследований Фибоначчи для получения более точного прогноза. Например, трейдер может наблюдать точки пересечения в сочетании дуг Фибоначчи и сопротивлений.
Исследования Фибоначчи часто используются в сочетании с другими формами технического анализа.Например, исследования Фибоначчи в сочетании с волнами Эллиотта могут использоваться для прогнозирования степени восстановления после различных волн. Надеюсь, вы сможете найти свою нишу для исследований Фибоначчи и добавить ее в свой набор инвестиционных инструментов.
7.2: Золотое сечение и последовательность Фибоначчи
В этом разделе мы обсудим очень особое число, называемое золотым сечением. Это иррациональное число, немного больше 1,6, и оно (что несколько удивительно) имело огромное значение в мире науки, искусства и музыки.Также было обнаружено, что это число имеет удивительную связь с так называемой последовательностью Фибоначчи, первоначально изученной в контексте биологии много веков назад. Эта неожиданная связь между алгеброй, биологией и искусством предполагает математическое единство мира и иногда также обсуждается в философии.
Золотое сечение
Для одного числа \ (a \) и другого меньшего числа \ (b \) соотношение этих двух чисел находится путем их деления.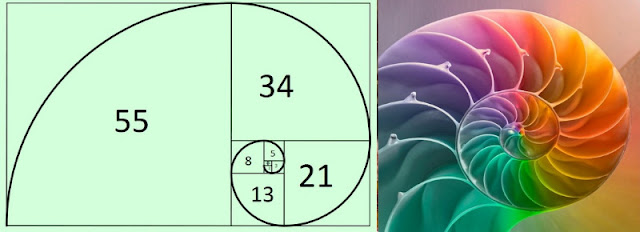
Их соотношение равно \ (a / b \).Другое соотношение получается сложением двух чисел \ (a + b \) и делением на большее число \ (a \). Новое соотношение — \ ((a + b) / a \). Если эти два соотношения равны одному и тому же числу, то это число называется золотым соотношением. Греческая буква \ (\ varphi \) (фи) обычно используется для обозначения золотого сечения.
Например, если \ (b = 1 \) и \ (a / b = \ varphi \), то \ (a = \ varphi \). Второе соотношение \ ((a + b) / a \) тогда будет \ ((\ varphi + 1) / \ varphi \). Поскольку эти два соотношения равны, это правда:
\ [\ varphi = \ dfrac {\ varphi + 1} {\ varphi} \ nonumber \]
(У этого уравнения есть два решения, но только положительное решение называется золотым сечением \ (\ varphi \)).
Один из способов написать это число —
\ [\ varphi = \ dfrac {1+ \ sqrt {5}} {2} \ nonumber \]
\ (\ sqrt {5} \) — положительное число, которое при умножении на само себя дает \ (5: \ sqrt {5} \ times \ sqrt {5} = 5 \).
Золотое сечение — иррациональное число. Если человек попытается записать его десятичное представление, оно никогда не остановится и никогда не создаст шаблон, но начнется так: 1.6180339887 … Интересная особенность этого числа заключается в том, что вы можете вычесть из него 1 или разделить 1 по нему, и результат будет таким же.
\ [\ varphi-1 = 1,6180339887 \ ldots-1 = 0,6180339887 \ nonumber \]
\ [1 / \ varphi = \ frac {1} {1.6180339887} = 0,6180339887 \ nonumber \]
Золотой прямоугольник
Если длина прямоугольника, деленная на его ширину, равна золотому сечению, то прямоугольник называется «золотым прямоугольником». Если квадрат отрезан от одного конца золотого прямоугольника, то другой конец будет новым золотым прямоугольником. На картинке большой прямоугольник (синий и розовый вместе) представляет собой золотой прямоугольник, потому что \ (a / b = \ varphi \).{2} \). Тогда мы получим \ (\ dfrac {a} {b} = \ dfrac {b} {a-b} \).
Обе стороны — \ (\ varphi \) .
Последовательность Фибоначчи
Последовательность Фибоначчи — это список чисел. Начните с 1, 1, а затем вы сможете найти следующее число в списке, сложив два последних числа вместе. Результирующая (бесконечная) последовательность называется последовательностью Фибоначчи. Поскольку мы начинаем с 1, 1, следующее число будет 1 + 1 = 2. Теперь у нас есть 1, 1, 2. Следующее число 1 + 2 = 3. Теперь у нас есть 1, 1, 2, 3. Следующее число 2 + 3 = 5.Следующее — 3 + 5 = 8 и так далее. Каждое из этих чисел называется числом Фибоначчи. Первоначально Фибоначчи (Леонардо Пизанский, живший около 800 лет назад) придумал эту последовательность для изучения популяций кроликов! Он, вероятно, понятия не имел, что произойдет, если вы разделите каждое число Фибоначчи на предыдущее, как показано ниже.
Число Фибоначчи | делится на число до | соотношение |
|---|---|---|
1 | ||
1 | 1/1 | = 1.0000 |
2 | 1/2 | = 2,0000 |
3 | 3/2 | = 1,5000 |
5 | 5/3 | = 1. |
8 | 8/5 | = 1,6000 |
13 | 13/8 | = 1,6250 |
21 | 21/13 | = 1.6154 … |
34 | 34/21 | = 1,6190 … |
55 | 55/34 | = 1,6177 … |
89 | 89/55 | = 1.6182 … |
… | … | … |
= 1,6180 … |
6667Вот очень удивительный факт:
Примечание
Отношение двух последовательных чисел Фибоначчи приближается к золотому сечению.
Оказывается, числа Фибоначчи довольно часто встречаются в природе. Некоторые примеры — узор листьев на стебле, части ананаса, цветение артишока, распускание папоротника и расположение сосновой шишки. Числа Фибоначчи также встречаются в генеалогическом древе пчел.
Между тем, многие художники и исследователи музыки изучали художественные произведения, в которых золотое сечение играет важную роль. К ним относятся работы Микеланджело, Да Винчи и Моцарта.Заинтересованные читатели могут найти в Интернете множество ресурсов и видео. Возможно, неудивительно, что числа вроде 3, 5, 8 и 13 очень важны в теории музыки; просто взгляните на клавиши пианино!
Номер ссылки
- Список литературы (17)
Авторы и авторство
φ Золотое сечение ★ Фибоначчи
Это отрывок из книги «Мастер Фибоначчи: человек, изменивший математику». Все цитаты занесены в каталог на странице «Цитаты».
ЗОЛОТОЕ СООТНОШЕНИЕ
(Предыдущий раздел: Phi )
Купить сейчас на AmazonДревнее соотношение Евклида на протяжении веков описывалось многими именами, но впервые было названо «золотым сечением» в девятнадцатом веке. Не очевидно, что Фибоначчи установил какую-либо связь между этим соотношением и последовательностью чисел, которую он нашел в задаче о кролике («Евклид»). Только в конце семнадцатого века связь между числами Фибоначчи и золотым сечением была доказана (и даже тогда не полностью) шотландским математиком Робертом Симсоном (1687-1768) (Livio 101).
Греческая буква тау (Ττ) на протяжении сотен лет представляла золотое сечение в математике, но недавно (в начале 20-го века) американскому математику Марку Барру, который выбрал первое соотношение, был присвоен символ фи ( Φ ) Греческая буква в имени великого скульптора Фидия (ок. 490–430 до н. Э.), Потому что считалось, что он использовал золотое сечение в своих скульптурах и в дизайне Парфенона (Доннеган; Ливио 5). [Правдивость этих и других утверждений (например, о том, что золотое сечение встречается в картинах, пирамидах Египта и измерениях пропорций человеческого тела) рассматривается в книге «Фибоначчи в искусстве и музыке.»] Немецкий математик Мартин Ом (брат физика Георга Симона Ома, в честь которого назван закон Ома) впервые использовал термин« золотое сечение »для описания этого отношения во втором издании своей книги Die Reine Elementar-Mathematik (The Pure Элементарная математика) (1835). Он писал: «Это разделение произвольной линии на две такие части обычно называют« золотым сечением »». Однако он не изобретал этот термин, поскольку сказал «обычно называет», указывая на то, что этот термин является общепринятым. принял тот, который использовал сам (Livio 6).
Купить сейчас на AmazonЧисло золотого сечения для phi (φ) составляет 0,61803 39887…, что коррелирует с соотношением, вычисляемым при делении числа в ряду Фибоначчи на его последующее число, например 34/55, а также число, полученное при делении крайней части строки на целое. Это число является обратной величиной 1,61803 39887… или Phi (Φ), что является соотношением, вычисляемым при делении числа в ряду Фибоначчи на предшествующее ему число, например, при делении 55/34 и при делении всей линии. по самому большому разделу.n) / (x — (1-x)), где x = (1 + sqrt 5) / 2 ~ 1,618.
Другой способ написать уравнение:
Следовательно, phi = 0,618 и 1 / Phi. Сила фи — это отрицательная сила фи. Одна из причин, по которой последовательность Фибоначчи очаровывала людей на протяжении веков, заключается в тенденции к тому, что отношения чисел в рядах падают либо на фи, либо на фи [после F (8)]. Другие обсуждали, может ли существовать сверхъестественное объяснение того, что кажется невероятным математическим совпадением.
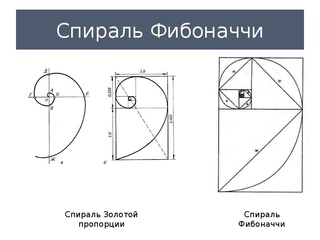
Спираль Фибоначчи
Границы квадратов последовательных чисел Фибоначчи создают спираль, известную как спираль Фибоначчи; он следует за поворотами под постоянным углом, который очень близок к золотому сечению. В результате ее часто называют золотой спиралью (Леви 121).
Золотая спиральНастоящая золотая спираль образована серией золотых прямоугольников с одинаковыми пропорциями, поэтому она не совсем такая же, как спираль Фибоначчи, но очень похожа.По мере того, как спираль Фибоначчи увеличивается в размере, она приближается к углу золотой спирали, потому что отношение каждого числа в ряду Фибоначчи к числу до того, как оно сходится к Phi , 1,618 по мере развития ряда (Meisner, «Spirals »).
Купить сейчас на AmazonМногие природные явления (например, вращение ураганов и спиральные рукава галактик) и объекты в природе, кажется, существуют в форме золотых спиралей; например, раковина наутилуса с камерами (Nautilus pompilius) и расположение семян в головке подсолнечника, очевидно, расположены по спирали, как и чешуйки шишек сосновых шишек (Knott, Brief; Livio 8).Спирали Фибоначчи, золотые спирали и спирали, основанные на золотом сечении, часто появляются в живых организмах. Однако не каждая спираль в природе связана с числами Фибоначчи или Фи; некоторые из этих спиралей являются равноугольными спиралями, а не спиралями Фибоначчи или золотыми спиралями. Равноугольная спираль обладает уникальными математическими свойствами, в соответствии с которыми размер спирали увеличивается, но объект сохраняет форму кривой при каждом последующем повороте. Числа Фибоначчи чаще всего встречаются в природе в количестве и расположении листьев вокруг стеблей растений, а также в расположении листьев, частей и семян цветов и других растений (Мейснер, «Спирали»).
Многие наблюдатели находят модели спиралей Фибоначчи и золотых спиралей эстетически более привлекательными, чем другие модели. Поэтому некоторые историки и изучающие математику придают исключительную ценность тем объектам и видам деятельности в природе, которые, кажется, следуют паттернам Фибоначчи.
Фибоначчи
ФибоначчиЭнди Нортон
Отделение Математическое образование
Университет Джорджии
* см. Другие примеры
Фибоначчи и золотое сечение
Связь между последовательностью Фибоначчи и золотое сечение удивительно.У нас есть два, казалось бы, не связанных между собой темы, производящие такое же точное количество. Учитывая, что это число (или золотое сечение) нерационально, возникновение выходит за рамки совпадение. Это требует дальнейшего изучения …Золотое сечение = (sqrt (5) + 1) / 2 или около 1,618 Золотое сечение, пожалуй, лучше всего отображается визуально. в золотом прямоугольнике. Этот прямоугольник обладает тем свойством, что его длина находится в соотношении Голена с шириной. Как следствие, мы можем разделить этот прямоугольник на квадрат и прямоугольник меньшего размера что похоже на первое.Пусть следующий набросок GSP проиллюстрирует:
Последовательность Фибоначчи — это последовательность, в которой определяется каждый член. как сумма двух предыдущих условий: Мы можем легко создать эту последовательность в электронной таблице, используя формулу выше. Это было сделано в центральной колонке. таблицы ниже:
| 1 | 1 | |
| 2 | 1 | 1 |
| 3 | 2 | 2 |
| 4 | 3 | 1.5 |
| 5 | 5 | 1.66666666666667 |
| 6 | 8 | 1,6 |
| 7 | 13 | 1,625 |
| 8 | 21 | 1,61538461538462 |
| 9 | 34 | 1,61 |
| 10 | 55 | 1.61764705882353 |
| 11 | 89 | 1,61818181818182 |
| 12 | 144 | 1,61797752808989 |
| 13 | 233 | 1.61805555555556 |
| 14 | 377 | 1.61802575107296 |
| 15 | 610 | 1.61803713527851 |
| 16 | 987 | 1.61803278688525 |
| 17 | 1597 | 1.61803444782168 |
| 18 | 2584 | 1.61803381340013 |
| 19 | 4181 | 1.61803405572755 |
| 20 | 6765 | 1.61803396316671 |
| 21 | 10946 | 1.6180339985218 |
| 22 | 17711 | 1.61803398501736 |
| 23 | 28657 | 1.61803396 |
| 24 | 46368 | 1.61803398820533 |
| 25 | 75025 | 1.6180339889579 |
| 26 | 121393 | 1.61803398867044 |
| 27 | 196418 | 1.61803398878024 |
| 28 | 317811 | 1.6180339887383 |
| 29 | 514229 | 1.61803398875432 |
| 30 | 832040 | 1.6180339887482 |
| 31 | 1346269 | 1.61803398875054 |
| 32 | 2178309 | 1.61803398874965 |
| 33 | 3524578 | 1.61803398874999 |
| 34 | 5702887 | 1.61803398874986 |
| 35 | 9227465 | 1.61803398874991 |
| 36 | 14930352 | 1.61803398874989 |
| 37 | 24157817 | 1.6180339887499 |
| 38 | 369 | 1.61803398874989 |
| 39 | 63245986 | 1.6180339887499 |
| 40 | 102334155 | 1.61803398874989 |
| 41 | 165580141 | 1.6180339887499 |
| 42 | 267914296 | 1.6180339887499 |
| 43 | 433494437 | 1.6180339887499 |
| 44 | 701408733 | 1.6180339887499 |
| 45 | 11340 | 1.6180339887499 |
| 46 | 1836311903 | 1.6180339887499 |
| 47 | 2971215073 | 1.6180339887499 |
| 48 | 4807526976 | 1.6180339887499 |
| 49 | 7778742049 | 1.6180339887499 |
| 50 | 12586269025 | 1.6180339887499 |
Понимание отношений Помните, теперь золотой прямоугольник можно разделить в квадрат и еще один золотой прямоугольник. Фактически, мы можем повторить этот процесс снова и снова. Предположим, мы начинаем с прямоугольника длиной Y и шириной X. Когда мы разделим этот прямоугольник на квадрат и новый золотой прямоугольник, получаем длину X и ширину Y-X для нового прямоугольника. Поскольку стороны прямоугольников равны в той же пропорции (а именно 1.618 …), получаем: Теперь вернемся к последовательности Фибоначчи. 0.5 * 0,5 + 0,5
Это пять в половинной степени, умноженная на половину плюс половина.
Связанный: 11 самых красивых математических уравнений
Phi тесно связан с последовательностью Фибоначчи , в которой каждое последующее число в последовательности находится путем сложения двух предыдущих чисел. Эта последовательность идет 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Это также связано со многими заблуждениями.
Взяв отношение последовательных чисел Фибоначчи, вы можете приближаться к фи. Интересно, что если вы расширите последовательность Фибоначчи назад — то есть до нуля и на отрицательные числа — соотношение этих чисел будет приближать вас к отрицательному решению, маленький фи -0,6180339887…
Существует ли золотое сечение в природа?
Хотя люди знали о фи уже давно, большую известность он приобрел только в последние столетия.По словам Нотта, итальянский математик эпохи Возрождения Лука Пачоли написал книгу под названием «De Divina Proportione» («Божественная пропорция») в 1509 году, в которой обсуждалась и популяризовалась фи.
Пачоли использовал рисунки, сделанные Леонардо да Винчи , которые включали фи, и возможно, что да Винчи был первым, кто назвал это «sectio aurea» (латинское «золотое сечение»). Только в 1800-х годах американский математик Марк Барр использовал греческую букву Φ (фи) для обозначения этого числа.
Как свидетельствуют другие названия числа, такие как божественная пропорция и золотое сечение, фи приписывают множество чудесных свойств. Писатель Дэн Браун включил длинный отрывок в свой бестселлер «Код да Винчи» (Doubleday, 2000), в котором главный герой обсуждает, как фи представляет собой идеал красоты и встречается на протяжении всей истории. Более трезвые ученые обычно опровергают подобные утверждения.
Например, энтузиасты фи часто упоминают, что некоторые измерения Великой пирамиды в Гизе , такие как длина ее основания и / или высота, находятся в золотом сечении.Другие утверждают, что греки использовали фи при проектировании Парфенона или в своих прекрасных скульптурах.
Энтузиасты Фи любят указывать на то, что пирамиды Гизы, построенные между 2589 и 2504 годами до нашей эры, были построены в золотом сечении. Но измерения по своей природе неточны и произвольны, поэтому пирамиды не являются точными примерами золотого сечения. (Изображение предоставлено Дэном Брекволдтом Shutterstock)Но, как Марковский указал в своей статье 1992 года в журнале College Mathematics Journal под названием «Заблуждения о золотом сечении»: «измерения реальных объектов могут быть только приблизительными.Поверхности реальных объектов никогда не бывают идеально плоскими ». Далее он написал, что неточности в точности измерений приводят к еще большим неточностям, когда эти измерения выражаются в соотношениях, поэтому заявления о древних зданиях или искусстве, соответствующих фи, должны приниматься с большой долей вероятности. крупица скепсиса
Часто говорят, что размеры архитектурных шедевров близки к фи, но, как отмечал Марковский, иногда это означает, что люди просто ищут отношение, которое дает 1,6, и называют это фи.Найти два отрезка с коэффициентом 1,6 не составляет особого труда. Выбор места для измерения может быть произвольным и при необходимости скорректирован, чтобы приблизить значения к фи.
Попытки найти фи в человеческом теле также поддаются подобным заблуждениям. В недавнем исследовании утверждалось, что золотое сечение обнаруживается в разных пропорциях человеческого черепа. Но, как сказал в интервью Live Science :
ведущий преподаватель анатомии человека в Медицинской школе Альперта (AMS) при Университете Брауна в Род-Айленде Дейл Риттер, ) наука… с таким количеством костей и таким количеством интересных точек на этих костях, я мог бы предположить, что где-то еще в человеческой скелетной системе будет хотя бы несколько «золотых соотношений».
Связано: Фотографии: большие числа, определяющие Вселенную
И хотя фи считается обычным явлением в природе, его значение преувеличено. Лепестки цветов часто имеют числа Фибоначчи, такие как пять или восемь, а сосновые шишки растут свои семена наружу по спирали чисел Фибоначчи. Но есть столько же растений, которые не следуют этому правилу, так и те, которые соблюдают, — сказал Live Science математик из Стэнфордского университета Кейт Девлин.
Люди утверждали, что морские ракушки, такие как ракушки наутилуса, обладают свойствами, присущими фи.Но, как указывает Девлин на своем веб-сайте , «наутилус действительно наращивает свою раковину по логарифмической спирали, то есть спирали, которая поворачивается на постоянный угол по всей своей длине, что делает его везде самоподобным. постоянный угол — это не золотое сечение. Жалко, я знаю, но вот оно. »
Хотя фи, безусловно, представляет собой интересную математическую идею, именно мы, люди, придаем значение тому, что мы находим во Вселенной. Защитник, смотрящий через очки цвета фи, может повсюду видеть золотое сечение.Но всегда полезно выйти за рамки конкретной точки зрения и спросить, действительно ли мир соответствует нашему ограниченному пониманию его.
Дополнительные ресурсы:
золотое сечение | Примеры, определение и факты
Золотое сечение , также известное как золотое сечение , золотая середина или божественная пропорция , в математике иррациональное число (1 + квадратный корень из √5) / 2 , часто обозначается греческой буквой ϕ или τ, что приблизительно равно 1.618. Это отношение отрезка линии, разрезанного на две части разной длины, при котором отношение всего сегмента к таковому более длинного сегмента равно отношению более длинного сегмента к более короткому. Происхождение этого числа можно проследить до Евклида, который упоминает его как «крайнее и среднее соотношение» в элементах . С точки зрения современной алгебры, если длина более короткого сегмента равна одной единице, а длина более длинного сегмента — x единиц, возникает уравнение ( x + 1) / x = x / 1; это может быть преобразовано в квадратное уравнение x 2 — x — 1 = 0, для которого положительное решение равно x = (1 + квадратный корень из √5) / 2, золотое сечение.
Древние греки признавали это свойство «разделения» или «разделения на части», фраза, которая в конечном итоге была сокращена до просто «раздел». Прошло более 2000 лет, когда и «сечение», и «сечение» были названы «золотыми» немецким математиком Мартином Омом в 1835 году. Греки также заметили, что золотое сечение обеспечивает наиболее эстетичную пропорцию сторон прямоугольника. , понятие, которое было расширено в эпоху Возрождения, например, благодаря работе итальянского эрудита Леонардо да Винчи и публикации De divina пропорционально (1509; Божественная пропорция ), написанной итальянским математиком Лукой Пачоли и проиллюстрированной Леонардо.
Витрувианский человек, рисунок Леонардо да Винчи ( ок. 1509), иллюстрирующий пропорциональный канон, установленный классическим римским архитектором Витрувием; в Академии изящных искусств Венеции.
Foto Marburg / Art Resource, New YorkЗолотое сечение встречается во многих математических контекстах. Его геометрически можно построить с помощью линейки и циркуля, и это происходит при исследовании архимедовых и платоновых тел. Это предел отношений последовательных членов последовательности чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13,…, в котором каждый член после второго является суммой двух предыдущих, а также значение самой основной из непрерывных дробей, а именно 1 + 1 / (1 + 1 / (1 + 1 / (1 + ⋯.
В современной математике золотое сечение встречается при описании фракталов, фигур, которые проявляют самоподобие и играют важную роль в изучении хаоса и динамических систем.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишись сейчасКомпульсивное содержание — Золотое сечение и последовательность Фибоначчи в искусстве
Итальянскому математику конца XI века Фибоначчи приписывают распространение арабской числовой системы в Европу и очень быстро его одноименную последовательность, комбинацию чисел, которая образовывалась из суммы двух предыдущих номеров (например, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т.