ТЕСТ №2 «Диаграммы и графики в электронных таблицах» — Тесты по информатике и ИКТ — Архив тестов — Каталог статей
ТЕСТ №2 «Диаграммы и графики в электронных таблицах»
1. Деловая графика представляет собой:
1. совокупность графиков функций;
2. графические иллюстрации;
3. график совещания;
4. совокупность программных средств, позволяющих представить в графическом виде закономерности изменения числовых данных.
- График функции можно создать в Excel при помощи:
1. Строки формул;
2. Мастера Функций;
3. Мастера Шаблонов;
4. Мастера Диаграмм.
- Гистограмма наиболее пригодна для:
1. отображения распределений;
2. отображения динамики изменения данных;
3. сравнения различных членов группы;
4. отображения удельных соотношений различных признаков.
- Диаграмма это:
1. карта местности;
2. форма графического представления числовых значений, которая позволяет облегчить интерпретацию числовых данных;
3. красиво оформленная таблица;
4. обычный график.
- Диаграмма в электронных таблицах – это:
1. качественно оформленная числовая таблица;
2. график, отображающий зависимость между всеми числами таблицы;
3. средство наглядного графического изображения информации, предназначенное для сравнения нескольких величин или нескольких значений одной величины, слежения за изменением их значений и т. п.
4. зависимость между числовыми значениями.
- Круговая диаграмма – это диаграмма:
- представленная в виде круга, разбитого на секторы, в которой допускается только один ряд данных;
- в которой отдельные ряды данных представлены в виде закрашенных разными цветами областей;
- в которой используется система координат с тремя координатными осями, что позволяет получить эффект пространственного представления рядов данных;
- в
которой отдельные значения представлены точками в декартовой состеме
координат.

- В каком разделе меню табличного процессора Excel находится Мастер Диаграмм:
1. Правка;
2. Вставка;
3. Сервис;
4. Данные.
- Форма графического представления числовых значений, позволяющая облегчить восприятие и интерпретацию числовых данных, называется:
1. чертежом;
2. картой;
3. блок-схемой;
4. диаграммой.
9. Гистограмма – это диаграмма, в которой:
1. отдельные значения представлены полосами различной длины, расположенными горизонтально вдоль оси ОХ
3. используется система координат с тремя координатными осями, что позволяет получить эффект пространственного представления рядов данных;
4. для представления отдельных значений используются параллелепипеды, размещенные вдоль оси ОХ.
10. Диаграмма, в которой отдельные значения представлены точками в декартовой системе координат, называется:
1. линейчатой;
2. точечной;
3. круговой;
4. гистограммой.
11. Линейчатая диаграмма – это диаграмма:
1. в которой отдельные значения представлены вертикальными столбиками различной высоты;
2. в которой отдельные значения представлены точками в декартовой системе координат;
3. в которой отдельные значения представлены полосами различной длины, расположенными горизонтально вдоль оси ОХ
4. представленная в виде круга, разбитого на секторы, и в которой допускается только один ряд данных.
12. Чтобы отформатировать какой-либо элемент диаграммы, необходимо:
1. дважды щелкнуть по нему курсором мыши;
2. выполнить команды Диаграмма, Исходные данные;
3. выполнить команды Диаграмма, Добавить данные;
4. все вышеперечисленные ответы верны.
все вышеперечисленные ответы верны.
13. На основе чего строится любая диаграмма?
а. книги Excel
б. графического файла
в. текстового файла
г. данных таблицы
14. Для сравнения нескольких величин в одной точке обычно используется:
1. линейчатая диаграмма;
2. гистограмма;
3. точечная диаграмма;
4. круговая диаграмма.
Панель Преобразование в Разработчике модели пригодности—ArcGIS Pro
Доступно с лицензией Spatial Analyst.
Используйте панель Преобразование в Разработчике модели пригодности, чтобы преобразовать значения каждого критерия к единой шкале пригодности. После того, как все критерии будут соответствующим образом преобразованы, их можно объединить для получения итоговой карты пригодности.
Компоненты панели Преобразование
На следующем изображении показана панель Преобразование.
Панель Преобразование и ее компоненты.
Панель Преобразование состоит из трех основных разделов. Центральная часть используется для указания метода преобразования. На панели слева отображается гистограмма пригодности. На панели справа отображается диаграмма преобразования. Обе панели предоставляют информацию, которая поможет вам выбрать наиболее подходящее преобразование.
Методы преобразования
В центральной части панели Преобразование перечислены три метода, которые можно использовать для преобразования критериев:
- Уникальные категории — это преобразование в шкалу пригодности методом один-к-одному. Подходит для категориальных данных, таких как землепользование.
- Диапазон классов — группирует диапазоны значений в классы и присваивает каждому классу значение пригодности. Подходит для непрерывных значений, когда одна и та же пригодность может быть назначена диапазону значений.
- Непрерывные функции — применяет линейные и нелинейные функции для преобразования входных значений.
 Подходит для непрерывных данных, таких как уклон, расстояние от водотоков и высота над уровнем моря.
Подходит для непрерывных данных, таких как уклон, расстояние от водотоков и высота над уровнем моря.
Гистограмма пригодности
Гистограмма пригодности дает представление о распределении значений пригодности в итоговой карте пригодности. Гистограмма и карта пригодности обновляются при каждом изменении модели. Гистограмма итоговой карты пригодности обеспечивает обратную связь, давая представление о том, как изменения в преобразовании повлияют на итоговый результат.
Диаграмма преобразования
Диаграмма преобразования обеспечивает обратную связь при определении преобразования. Она показывает, как входные значения критерия будут преобразованы в шкалу пригодности.
На диаграмме ось x содержит входные значения базового критерия, а ось y отображает шкалу пригодности. Отображается гистограмма значений базового критерия. Если вы выберете метод Непрерывных функций из центральной части, применяемая функция будет наложена на гистограмму. Диаграмма обновляется всякий раз, когда меняется метод преобразования в центральной части или меняются какие-либо настройки.
Запуск преобразования
При выборе каждого преобразования создается цепочка растровых функций. Для динамического создания итоговых слоев преобразования и пригодности цепочка растровых функций запускается с использованием разрешения экрана и для текущего экстента отображения.
Чтобы запустить модель в полном разрешении, нажмите кнопку Запустить во вкладке Пригодность. Преобразования в цепочке функций растра вычисляются в полном разрешении, что дает более точные результаты.
Преобразованные данные не сохраняются до тех пор, пока слой преобразования не будет сохранен в полном разрешении. На панели Преобразование отметьте опцию Сохранить преобразованный набор данных при запуске модели. Нажмите кнопку , затем перейдите к папке, в которой вы хотите сохранить слой преобразования, и выберите ее. Укажите имя набора данных и нажмите кнопку Сохранить.
Связанные разделы
Отзыв по этому разделу?
Освоение среды табличного процессора Microsoft Excel
Электронная таблица – это прикладная программа, предназначенная для обработки структурированных в виде таблицы данных
Электронная таблица предназначена для обработки преимущественно числовых данных, структурированных с помощью таблиц
А) именуются пользователями произвольным образом;
Б) обозначаются буквами русского алфавита;
В) обозначаются буквами латинского алфавита;
Г) нумеруются.
Для пользователя ячейка электронной таблицы идентифицируются путем последовательного указания имени столбца и номера строки, на пересечении которых располагается ячейка
Вычислительные формулы в ячейках электронной таблицы записываются специальным образом с использование встроенных функций и по правилам, принятым
А) 5(A2+C3)/3(2B2-3D3) ;
Б) 5*(A2+C3)/3*(2*B2-3*D3) ;
В) 5*(A2+C3)/(3*(2*B2-3*D3)) ;
Г) 5(A2+C3)/(3(2B2-3D3)) .
А) C3+4*D4
Б) C3=C1+2*C2
В) A5B5+23
Г) =A2*A3-A4
А) не изменяются;
Б) преобразуются вне зависимости от нового положения формулы;
В) преобразуются в зависимости от нового положения формулы;
Д) преобразуются в зависимости от правил указанных в формуле.
А) преобразуются вне зависимости от нового положения формулы;
Б) преобразуются в зависимости от длины формулы;
В) не изменяются;
Г) преобразуются в зависимости от нового положения формулы.
Тест по теме «Графики и диаграммы в среде табличного процессора»
Деловая графика представляет собой совокупность программных средств, позволяющих представить в графическом виде закономерности изменения числовых данных.
Диаграмма — это
Какой тип диаграммы, как правило, используется для построения обычных графиков функций:
а) гистограмма;
б) линейчатая диаграмма;
в) точечная диаграмма;
г) круговая
диаграмма.
Линейчатая диаграмма — это диаграмма, в которой отдельные значения представлены полосами различной длины, расположенными горизонтально вдоль оси Х
Гистограмма — это диаграмма, в которой отдельные значения представлены вертикальными столбцами различной высоты
Круговая диаграмма — это диаграмма, представленная в виде круга разбитого на секторы, и в которой допускается только один ряд данных
Как и почему вы используете гистограмму изображения?
Хотя на этот вопрос не может быть «правильного» ответа, есть «правильные» ответы. Гистограмма — это мощный инструмент, и когда вы поймете, как его эффективно использовать, он может значительно помочь вашей фотографии.
Как вы упомянули, гистограмма — это представление тонального диапазона и распределения на фотографии. Основная механика как таковая:
- Гистограмма представляет тональный диапазон слева направо, с черными и оттенками слева, прогрессирующими через средние тона в середине, до светлых участков справа.
- «Громкость» любого данного тона представлена высотой вертикальной линии, которая представляет этот тон.
- Вертикальная линия на самом левом конце указывает на объем общих черных тонов
- Вертикальная линия в самом правом конце указывает на объем полных светлых тонов
- Вертикальная линия в самом центре указывает на объем 18% серых тонов
- Тоны для изображения берутся из интенсивности каждого пикселя (цветность или оттенок игнорируется, и измеряется только яркость / яркость / яркость)
- Общее количество тонов в изображении зависит от битовой глубины изображения
- 8-битное (24-битное) изображение имеет 256 различных тонов
- Изображение RAW в 12 бит / с (36 бит) имеет в общей сложности 4096 различных тонов
- RAW-изображение с 14 битами на дюйм (42 бита) имеет в общей сложности 16 384 различных тона
- 16-битное (48-битное) изображение RAW имеет в общей сложности 65 536 различных тонов
- 32-битное (96-битное) HDR-изображение эффективно отображает бесконечный тональный диапазон.
 38. В более реальных числах тональный диапазон варьируется от черного до очень тусклого звездного света (0,00001 ), через внутреннее освещение (1-10), через освещенную солнцем улицу (1 000 000), до яркости самого солнца (100 000 000) и далеко за ее пределами. Все эти значения могут быть представлены в одном HDR-изображении.)
38. В более реальных числах тональный диапазон варьируется от черного до очень тусклого звездного света (0,00001 ), через внутреннее освещение (1-10), через освещенную солнцем улицу (1 000 000), до яркости самого солнца (100 000 000) и далеко за ее пределами. Все эти значения могут быть представлены в одном HDR-изображении.)Учитывая эти факты о гистограмме, существует множество информации, которую вы можете получить из одной:
Контрастность — это мера различия между самыми яркими и самыми темными тонами. Чем больше диапазон охватывает гистограмма между левым и правым краями, тем больше контраст изображения:
Клавиша — это грубая мера яркости изображения, при этом верхняя клавиша становится ярче, а нижняя — темнее.
Если гистограмма сгруппирована в основных моментах, у вас есть изображение светлого тона:
Если гистограмма сгруппирована в тени и тени, у вас есть сдержанное изображение:
Очевидно, что если гистограмма распределяется равномерно, вы получаете сбалансированную экспозицию:
(Гистограмма, проходящая вверх по правой стороне гистограммы, вероятно, указывает на передержку — обрезанные блики. Гистограмма, проходящая вверх по левой стороне гистограммы, вероятно, указывает на недодержку — заблокированные тени.)
При использовании цветной гистограммы конвергенция красного, зеленого и синего пиков является показателем баланса белого. В частности, смещение основных голубых пиков может быть сильным индикатором теплоты или прохлады фотографии:
- Синие пики, смещенные вправо, указывают на более холодный тон изображения
- Синие пики, смещенные влево, указывают на более теплые тона изображения
- Синие пики в непосредственной близости от красных и желтых пиков указывают на слегка теплое изображение
На правильно сбалансированном белом изображении синий цвет обычно немного правее красных и желтых пиков.

Баланс и высота пиков на гистограмме являются показателем тонального диапазона и тонального баланса. Части гистограммы, которые являются очень низкими (долины), указывают на очень низкую громкость для этих тонов. Части гистограммы, которые являются очень высокими (пики), указывают на очень высокую громкость для этих тонов.
Базовая цветная гистограмма часто показывает серый, красный, синий и зеленый. Более продвинутая цветная гистограмма может также показывать желтый, пурпурный, голубой.
Цветные пики являются показателем объема тех заданных основных цветов, горизонтальное положение цветного пика является показателем тона цветов этого конкретного основного или основного цвета.
Серый цвет указывает на баланс основных цветов в этих тонах. Пики неосновного цвета (или линии частичной высоты), такие как желтый, пурпурный и голубой, указывают на смешение двух основных цветов в этих тонах.
РЕДАКТИРОВАТЬ
Как упомянул Джордан Х., есть хитрость, называемая « выставить направо » (или ETTR ), которая может быть полезна для получения оптимальных данных RAW. При съемке сцены, особенно тех, которые имеют широкий диапазон контраста, который может находиться на границе или, возможно, немного выше, динамического диапазона 5-6 ступеней цифровой камеры, захват достаточного тонального диапазона в тенях может быть затруднен.
Это связано с ограничениями большинства современных цифровых датчиков и тем, что они более чувствительны к бликам, чем к теням. «Экспозиция вправо» — это метод, при котором вы слегка переэкспонируете свои снимки на 1/3 — 1/2 шага (что, в свою очередь, смещает вашу гистограмму вправо … в сторону бликов), может помочь смягчить эти ограничения.
Экспозиция вправо также может помочь устранить проблемы с шумом в более темных частях ваших изображений. Следует отметить, что для правильного изображения необходимо использовать формат RAW, так как только в режиме raw вы сохраняете достаточно информации, чтобы исправить переэкспонирование во время постобработки, чтобы вернуть изображение в нормальный диапазон.
 Преимущество этого метода заключается в том, что он позволяет фиксировать детали, которые в противном случае были бы потеряны, без необходимости прибегать к фильтрам градуировки ND или другим более экстремальным мерам.
Преимущество этого метода заключается в том, что он позволяет фиксировать детали, которые в противном случае были бы потеряны, без необходимости прибегать к фильтрам градуировки ND или другим более экстремальным мерам.Это руководство, это просто руководство. Благодаря новым датчикам камеры динамический диапазон улучшается, а захват большего диапазона контраста в сцене одним кадром становится проще. Однако, даже когда динамический диапазон цифрового датчика улучшается, всегда будут моменты, когда нам нужно стрелять «на грани» или что это возможно, и такие приемы, как стрельба вправо, всегда будут полезны.
Тест по теме «Графики и диаграммы в среде табличного процессора»
Тест по теме «Графики и диаграммы в среде табличного процессора» 1. Деловая графика представляет собой: а) график совещания; б) графические иллюстрации; в) совокупность графиков функций; г) совокупность программных средств, позволяющих представить в графическом виде закономерности изменения числовых данных. 2. Диаграмма — это: а) форма графического представления числовых значений, которая позволяет облегчить интерпретацию числовых данных; б) график; в) красиво оформленная таблица; г) карта местности. 3. Какой тип диаграммы, как правило, используется для построения обычных графиков функций: а) гистограмма; б) линейчатая диаграмма; в) точечная диаграмма; г) круговая диаграмма. 4. Линейчатая диаграмма — это: а) диаграмма, в которой отдельные значения представлены полосами различной длины, расположенными горизонтально вдоль оси Х; б) диаграмма, отдельные значения которой представлены точками в декартовой системе координат; в) диаграмма, в которой отдельные значения представлены вертикальными столбиками различной высоты; г) диаграмма, представленная в виде круга разбитого на секторы, и в которой допускается только один ряд данных. 5. Гистограмма — это: а) диаграмма, в которой отдельные значения представлены вертикальными столбцами различной высоты; б) диаграмма, для представления отдельных значений которой используются параллелепипеды, размещенные вдоль оси Х; в) диаграмма, в которой используется система координат с тремя координатными осями, что позволяет получить эффект пространственного представления рядов данных.
 ;
г) диаграмма, в которой отдельные значения представлены
полосами различной длины, расположенными горизонтально вдоль
оси Х.
6. Круговая диаграмма — это:
а) диаграмма, представленная в виде круга разбитого на секторы,
и в которой допускается только один ряд данных;
б) диаграмма, отдельные значения которой представлены точками
в декартовой системе координат;
в) диаграмма, в которой отдельные ряды данных представлены в
виде закрашенных разными цветами областей;
г) диаграмма, в которой используется система координат с тремя
координатными осями, что позволяет получить эффект
пространственного представления рядов данных.
7. Диаграмма, отдельные значения которой представлены точками в
декартовой системе координат, называется:
а) линейчатой;
б) точечной;
в) круговой;
г) гистограммой.
8. Гистограмма наиболее пригодна для: а) для отображения распределений;
б) сравнения различных членов группы;
в) для отображения динамики изменения данных;
3
;
г) диаграмма, в которой отдельные значения представлены
полосами различной длины, расположенными горизонтально вдоль
оси Х.
6. Круговая диаграмма — это:
а) диаграмма, представленная в виде круга разбитого на секторы,
и в которой допускается только один ряд данных;
б) диаграмма, отдельные значения которой представлены точками
в декартовой системе координат;
в) диаграмма, в которой отдельные ряды данных представлены в
виде закрашенных разными цветами областей;
г) диаграмма, в которой используется система координат с тремя
координатными осями, что позволяет получить эффект
пространственного представления рядов данных.
7. Диаграмма, отдельные значения которой представлены точками в
декартовой системе координат, называется:
а) линейчатой;
б) точечной;
в) круговой;
г) гистограммой.
8. Гистограмма наиболее пригодна для: а) для отображения распределений;
б) сравнения различных членов группы;
в) для отображения динамики изменения данных;
3Контрольная работа по «Информатике»
· в которой используется система координат с тремя координатными
осями, что позволяет получить эффект пространственного
представления рядов данных;
26 Диаграмма, в которой отдельные значения представлены точками в
декартовой системе координат, называется:
· Линейчатой;
· Точечной;
· Круговой;
· Гистограммой;
27 Гистограмма наиболее пригодна для:
· отображения распределений;
· сравнения различных членов группы;
· отображения динамики изменения данных;
· отображения удельных соотношений различных признаков;
28. В ячейку электронной таблицы нельзя
внести: · Текст;
· Формулу;
· Иллюстрацию;
29. Операндами формулы в электронных
таблицах могут быть: · математические функции;
· константы;
· все перечисленное
30. Пользователь может сортировать в
электронной таблице: · все перечисленное;
· ячейки столбца;
· ячейки строки;
31.
 Excel-это:
Excel-это:· графический редактор;
· СУБД;
· электронные таблицы;
· операционная система;
32 Сколько максимально в рабочей книге может
размещаться рабочих листов:
· 1000;
· 255;
· 10;
33 Сколько строк в рабочем листе:
· 20000;
· 16384;
· 500;
34. В какую категорию входит функция СУММ:
· Математическую;
· Статистическую;
· Финансовую
35. Какое расширение имеет файл Excel:
· Txt;
· Xls;
· Doc;
36. Что делает функция СРЗНАЧ
· Закрашивает;
· Складывает;
· находит среднее значение;
37. Табличный процессор Excel написан для среды:
· Windows;
· Dos;
· Unix;
38 Назначение Excel –
· проведение расчетов;
· проведение расчетов, решение оптимизационных задач;
· проведение расчетов, решение оптимизационных задач,
построение диаграмм;
· проведение расчетов, решение оптимизационных задач,
построение диаграмм, создание web-документов;
39. Каждый документ представляет собой
· рабочие листы;
· рабочую книгу;
· набор таблиц;
40 Электронная таблица состоит из
· Таблиц;
· Столбцов;
· столбцов и строк;
· строк;
41 Укажите допустимые номера ячеек
· A1;
· В2;
· 23FD;
· C31Z;
42. В ячейке могут храниться данные
следующих типов · текстовые, графические, числовые и формулы;
· числовые и формулы;
· тестовые и формулы;
· числовые, текстовые и формулы;
43. Формула в электронных таблицах может включать
· имена ячеек;
· числа;
· текст;
· знаки арифметических операций;
· картинки;
44.
 В электронных
таблицах со знака «=» начинается
ввод
В электронных
таблицах со знака «=» начинается
ввод· Числа;
· Текста;
· Строки;
· Формулы;
45 В электронной таблице выделены ячейки A1:B3. Сколько ячеек
выделено?
· 3;
· 4;
· 5;
· 6;
46 В электронных таблицах выделена группа
ячеек A2:C4. Сколько ячеек входит в эту группу?
· 6;
· 7;
· 8;
· 9;
47. Для работы с областью в электронных
таблицах ее необходимо · Выделить;
· Удалить;
· Переместить;
· Передвинуть;
48. Адрес ячейки электронной таблицы – это
· любая последовательность символов;
· номер байта оперативной памяти, отведенного под ячейку;
· имя, состоящее из имени столбца и номера строки;
· адрес байта оперативной памяти, отведенного под ячейку;
· адрес машинного слова оперативной памяти, отведенного под
ячейку;
49 Можно ли на одном листе создавать
несколько диаграмм? · Да, любое количество;
· Да, любое количество только для таблиц, расположенных на этом
листе;
· Да, любое количество только для таблиц, расположенных в этой
книге;
· Нет;
50 При нажатии клавиши Delete по выделенной ячейке
выполнятся операция:
· полная очистка ячейки;
· редактирование ячейки;
· удаление ячейки;
· очистка содержимого ячейки;
51 В Excel записана формула =СУММ(A1;C3). Данные из какого
количества ячеек суммируются по этой формуле?
· 9 ;
· 2;
· 3;
· 6;
52 Ссылка с адресом $B$5 называется
· Относительной;
· Абсолютной;
· Смешанной;
Список использованной литературы
Методы построения динамических диаграмм в Excel Текст научной статьи по специальности «Компьютерные и информационные науки»
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
№ 1(4), 2015
Scientific journal
PHYSICAL AND MATHEMATICAL EDUCATION
Has been issued since 2013.

Науковий журнал
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА
Видається з 2013.
http://fmo-journal.fizmatsspu.sumy.ua/
Шамшина Н. Методы построения динамических диаграмм в Excel // Фізико-математична освіта. Науковий журнал. — Суми : СумДПУ ім. А.С.Макаренка, 2015. -№ 1 (4). — С. 39-46.
УДК 372.8+004.9
Наталья Шамшина
Сумский государственный педагогический университет имени А.С. Макаренко,
Украина
МЕТОДЫ ПОСТРОЕНИЯ ДИНАМИЧЕСКИХ ДИАГРАММ В EXCEL
Табличный процессор Excel из пакета Microsoft Office является наиболее популярной программой общего пользования для обработки и анализа числовых данных. Использование Excel для расчетов, математического моделирования, подготовки документов или в качестве базы данных общеизвестно. Однако, в это приложение заложен большой потенциал, позволяющий эффективно использовать его для графического анализа данных с помощью всевозможных диаграмм и графиков разного типа и различной сложности. В последнее время возросла популярность использования построенных в Excel динамических диаграмм для графического анализа большого объема статистических данных.
Анализ литературных источников, статей, заметок на Интернет-форумах показывает, что интерес к построению динамических диаграмм неизменно высок на протяжении длительного периода времени и не убывает. Более того, в последние годы задачи на построение динамических диаграмм встречаются среди олимпиадных заданий по информационным технологиям для школьников.
 Это говорит о том, что прогресс в области информационных технологий приводит к расширению сферы их применения и, соответственно, к востребованности специалистов, владеющих современными технологиями обработки и анализа данных. Таким образом возникает необходимость подготовки учителей, владеющих знаниями и методикой обучения построения динамических диаграмм и, соответственно, корректировки и обновления содержания курса информатики в высшей школе.
Это говорит о том, что прогресс в области информационных технологий приводит к расширению сферы их применения и, соответственно, к востребованности специалистов, владеющих современными технологиями обработки и анализа данных. Таким образом возникает необходимость подготовки учителей, владеющих знаниями и методикой обучения построения динамических диаграмм и, соответственно, корректировки и обновления содержания курса информатики в высшей школе.В сети Интернет можно найти достаточно много электронных публикаций, которые посвящены построению динамических диаграмм. Это, например, уроки дистанционных курсов «MS Excel для бизнеса» [2], страницы сайта «Путь воина. Менеджерами не рождаются, менеджерами становятся» [1], статьи в электронном журнале «Финансовый директор» [3], а также большое количество материалов на
39
PHYSICAL & MATHEMATICAL EDUCATION
№ 1(4), 2015
сайтах, предназначенных не только для экономистов, но и для самых разных пользователей, желающих профессионально работать в Excel [4].
В результате анализа публикаций можно утверждать, что обучение построению динамических диаграмм осуществляется методом детального рассмотрения практических примеров, реализующих те или иные стандартные экономические задачи. Для мотивированного менеджера-экономиста высшего или среднего звена, который сталкивается с аналогичными задачами в повседневной работе, этого вполне достаточно. Однако, несмотря на педагогическое мастерство авторов, проявляющееся в четкости и ясности изложения, для подготовки студентов первых курсов или старших школьников такой подход малоэффективен.
Таким образом, проблема анализа, систематизации, описания основных принципов и методов построения динамических диаграмм в Excel требует своего решения.
 Методические разработки по изучению данной темы в курсе информатики в сети не представлены.
Методические разработки по изучению данной темы в курсе информатики в сети не представлены.Цель данной статьи — рассмотреть понятие динамических диаграмм, их свойства и преимущества, описать общие принципы и методы построения динамических диаграмм в Excel. А также представить несколько примеров динамических диаграмм, изучаемых студентами в рамках лабораторной работы при изучении табличного процессора Excel в курсе информатики.
Диаграмма — графическое отображение числовых рядов данных. Ряд данных -непрерывная последовательность чисел в пределах одной строки или столбца таблицы. На диаграмме присутствуют необходимые пояснения, а именно — названия рядов данных, легенда, подписи категорий. Категории — названия точек ряда. Легенда — условные обозначения рядов данных, которые необходимы при отображении нескольких рядов данных. Термин «динамическая диаграмма» получил распространение, в первую очередь, в среде специалистов, занимающихся решением стандартных экономических задач нетривиальными методами.
Графические способы отображения числовых данных находят большое применение в экономическом анализе и статистике. Они используются в целях наглядного отображения экономических явлений, выявления взаимосвязей между обобщающими показателями и влияющими на них факторами и т.д. Графические изображения имеют большое иллюстративное значение, являются доходчивыми и понятными. В отличие от аналитических таблиц графики и диаграммы наглядно представляют основополагающие тенденции развития изучаемого экономического явления, дают возможность в образной форме показать закономерности развития этого явления.
Преимущество диаграмм перед другими типами информации заключается в том, что они позволяют быстро сделать логический вывод из большого количества данных. Сами по себе цифры в аналитических таблицах не являются достаточно наглядными, а если их много, они не производят должного впечатления.
 Кроме того, графическое изображение позволяет осуществить контроль достоверности полученных данных, так как на графике достаточно ярко проявляются возможные неточности, которые могут быть связаны с ошибками на каком-либо этапе проведения исследования.
Кроме того, графическое изображение позволяет осуществить контроль достоверности полученных данных, так как на графике достаточно ярко проявляются возможные неточности, которые могут быть связаны с ошибками на каком-либо этапе проведения исследования.Качественная визуализация большого объема информации — это почти всегда нетривиальная задача, т.к. отображение всех данных часто приводит к перегруженности диаграммы, ее запутанности и, в итоге, к неправильному восприятию и выводам. Идея отображения части данных в зависимости от выбора пользователя привела к появлению интерактивных «живых» диаграмм, управляемых пользователем.
40
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
№ 1(4), 2015
В некоторых случаях стандартных свойств обычных неподвижных диаграмм и графиков бывает недостаточно. С целью повышения информативности, возникла еще одна идея: к обычным свойствам статичных диаграмм добавить свойство подвижности и изменения, то есть, представить диаграммы в виде интерактивной анимации.
Управление отображением отдельных данных на диаграмме частично реализовано в так называемых сводных диаграммах Excel, где отображение рядов данных и точек ряда осуществляется с помощью управляющих кнопок на диаграмме. Особенность сводных диаграмм в том, что они служат исключительно для отображения подведенных итогов, так как строятся на основании сводных таблиц, являющихся результатом итогового анализа — суммы чисел по столбцу таблицы, среднего, максимума, минимума и т.д. Для наглядного отображения рядов данных, которое дает возможность оценить поведение анализируемых величин, тенденции их изменения, взаимозависимость, сводные диаграммы не пригодны.
Возникла необходимость найти другие методы, которые обеспечивают интерактивность, подвижность, изменяемость обычных диаграмм.
 Спрос вызывает предложение. В сети появились описания креативных решений задач по визуализации больших массивов данных экономической статистики с помощью обычных диаграмм Excel, которые обладают свойством подвижности, изменяемости. Возникло и общее название для них — динамические диаграммы. Динамическая — означает меняющаяся, движущаяся, отображающая разные диапазоны большого массива данных в зависимости от настроек пользователя. Динамическая диаграмма интерактивна, содержит элементы управления для выбора и уточнения диапазонов отображения данных.
Спрос вызывает предложение. В сети появились описания креативных решений задач по визуализации больших массивов данных экономической статистики с помощью обычных диаграмм Excel, которые обладают свойством подвижности, изменяемости. Возникло и общее название для них — динамические диаграммы. Динамическая — означает меняющаяся, движущаяся, отображающая разные диапазоны большого массива данных в зависимости от настроек пользователя. Динамическая диаграмма интерактивна, содержит элементы управления для выбора и уточнения диапазонов отображения данных.Динамические диаграммы характеризуют динамику, то есть изменения количественной оценки величины в течение известных периодов времени. С этой целью могут применяться любые из представленных в Excel типов диаграмм -гистограммы, линейчатые, графики, с областями, круговые, лепестковые и их подтипы. Чаще всего используются диаграммы-графики, именно они больше всего подходят для отображения большого количества точек ряда. Диаграммы-графики могут отображать несколько рядов данных. Данный тип диаграммы служит для отображения трендов по времени: по годам, по месяцам, по дням или по категориям. На таких диаграммах изменение количественной оценки изображается определенной линией-графиком, которая выражает непрерывность происходящего процесса. На оси абсцисс графика изображаются определенные периоды времени, а на оси ординат — соответствующие величины за рассматриваемые периоды времени в соответствии с принятым числовым масштабом.
Принципиальный подход к выбору методов построения динамической диаграммы зависит от конкретной ситуации, то есть, от количества данных, которые необходимо визуализировать, и от целей анализа. Целью может быть сравнение графиков нескольких величин на определенном промежутке времени, или анализ поведения графика на разных промежутках времени, или то и другое вместе. Часто для качественного анализа бывает необходимо увидеть общие тенденции как бы издалека, на большом промежутке времени, и тут же рассмотреть участок графика более детально, на маленьком промежутке времени, то есть применить масштабирование.

Рассмотрим основные принципы построения динамических диаграмм и методы их реализации для достижения указанных целей.
Для того, чтобы сравнивать ряды данных необходимо их отображать на диаграмме одновременно. При этом большое количество рядов данных загромождает
41
PHYSICAL & MATHEMATICAL EDUCATION
№ 1(4), 2015
диаграмму, мешая правильному восприятию. В этом случае нужно дать возможность пользователю выбирать ряды данных для отображения, например, по одному, по два или по три ряда.
Методы построения применяют элементы управления с ленты «Разработчик» и встроенные функции для выбора данных в диапазоне. В случае большого количества рядов данных, для выбора конкретных рядов используют следующие элементы управления — флажок, список. Для реализации интерактивности диаграмма строится по отдельной, специально созданной таблице с формулами, которая отображает только нужные данные. В эту дополнительную таблицу переносятся те исходные данные, которые пользователь выбрал с помощью элементов управления. Для переноса данных используют функции — ВПР(), ГПР(), ЕСЛИ().
Чтобы наблюдать график на равных промежутках времени последовательно слева-направо или наоборот, необходимо использовать равные смещающиеся диапазоны точек на оси абсцисс графика. При этом использовать как бы движущийся диапазон для построения графика.
Чтобы масштабировать график, необходимо использовать разные по величине диапазоны точек на оси абсцисс графика. При этом большое количество точек ряда соответствует меньшему масштабу, как бы взгляду издалека, а маленькое количество точек ряда соответствует большему масштабу, для более детального рассмотрения.
 ;К) задают диапазоны данных и подписей для выделенного ряда диаграммы: X — адрес ячейки с именем
;К) задают диапазоны данных и подписей для выделенного ряда диаграммы: X — адрес ячейки с именемY
— диапазон подписей категорий; Z — диапазон значений; K — порядковый номер ряда на диаграмме. Именно из-за особенностей функции РЯД() приходится создавать отдельные динамические диапазоны для значений и подписей категорий.
Комбинирование нескольких элементов управления или разных типов диаграмм (например, гистограммы и круговой диаграммы) позволяют удобно и наглядно отобразить для графического анализа любые статистические данные большого объема. Таким образом строится полностью интерактивная диаграмма, где можно отобразить именно тот фрагмент данных, который нужен для анализа.
Рассмотрим пример интерактивной динамической диаграммы для выбора конкретных рядов данных (рис.1а, 1б). Диаграмма показывает распределение расходов по разным категориям (продукты, лекарства, транспорт, ком-усл, другое) за
42
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
№ 1(4), 2015
месяц. Исходная таблица содержит данные за 12 месяцев. Выбор ряда — конкретного месяца осуществляется с помощью списка.
Рис. 1а. Динамическая диаграмма при выбранном месяце «січень»
січень
лютий
березень
квітень
травень
червень
липень
серпень
вересень
жовтень
листопад
грудень
Рис.
 1б. Динамическая диаграмма при выбранном месяце «вересень»
1б. Динамическая диаграмма при выбранном месяце «вересень»Следующий пример демонстрирует интерактивную динамическую диаграмму для движущегося диапазона построения графика, который можно масштабировать (рис.2а, 2б). Диаграмма показывает ежедневные изменения курсов валют. Исходная таблица содержит данные за 12 месяцев, от 1.01.14 до 31.12.14, то есть 356 значений. Выбор ряда — конкретной валюты осуществляется с помощью флажков. Изменение масштаба и перемещение по оси времени осуществляется с помощью ползунков.
Рамки статьи не позволяют рассмотреть все примеры динамических диаграмм, которые используются в лабораторной работе. Однако, данные примеры дают представление об уровне сложности заданий и их адаптации к процессу обучения студентов физико-математических специальностей педагогических ВУЗов.
В результате проведенного исследования скорректировано содержание курса по изучению табличного процессора для студентов педагогического университета физикоматематического факультета. Добавлена лабораторная работа на тему «Построение динамических диаграмм в Excel». В инструкции к работе объясняется назначение и преимущества динамических диаграмм, на примерах рассматриваются способы построения основных типов динамических диаграмм от простого к сложному. Задания лабораторной работы направлены на закрепление полученных знаний и выработку навыков работы в Excel, необходимых для построения динамических диаграмм: создание элементов управления и именованных диапазонов, использование формул выборки и анализа данных, редактирование и форматирование диаграмм разных типов.
43
PHYSICAL & MATHEMATICAL EDUCATION
№ 1(4), 2015
Рис.
 2а. Динамическая диаграмма изменения двух валют в диапазоне
2а. Динамическая диаграмма изменения двух валют в диапазонеот 10.08.14 до 26.10.14
Рис.2б. Динамическая диаграмма изменения одной валюты в диапазоне
от 1.04.14 до 27.04.14
Изучение динамических диаграмм требует от студентов определенных навыков работы с формулами, функциями, диаграммами, предварительного знакомства с элементами управления. Поэтому, лабораторную работу на построение динамических диаграмм в Excel целесообразно проводить в конце курса обучения с целью повторения пройденного материала и изучения нового.
Выводы. Польза и привлекательность интерактивных динамических диаграмм состоит в качественной визуализации большого объема информации, которая позволяет, не загромождая диаграмму, подстраиваться под желания пользователя. А именно:
— включать-выключать отображение отдельных рядов данных на выбор
— двигаться по оси категорий вперед-назад, отображая выбранный диапазон данных
44
ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)
№ 1(4), 2015
— масштабировать, то есть, приближать-удалять область построения диаграммы для изучения графика подробно в деталях или в целом
— комбинировать разные типы диаграмм для одновременного отображения детальных и итоговых данных.
Освоение методов построения динамических диаграмм при изучении табличного процессора Excel не только готовит студентов к дальнейшей профессиональной деятельности и повышает их уровень компетентности, а также развивает творческое воображение и активизируют познавательную деятельность.
 Динамические диаграммы, которые являются результатом выполнения заданий, сами по себе настолько привлекательны и удивительны, что неизменно вызывают положительную мотивацию студентов в дальнейшем освоении современных информационных технологий. Результат обучения при этом объединяет в себе интеллектуальную и практическую составляющую образования.
Динамические диаграммы, которые являются результатом выполнения заданий, сами по себе настолько привлекательны и удивительны, что неизменно вызывают положительную мотивацию студентов в дальнейшем освоении современных информационных технологий. Результат обучения при этом объединяет в себе интеллектуальную и практическую составляющую образования.Список использованных источников
1. Багузин С. В. Сайт «Путь воина. Менеджерами не рождаются, менеджерами становятся» [Электронный ресурс]: Режим доступа: http://baguzin.ru/wp/
2. Стыгарь А. Дистанционный курс на тему: «MS Excel для бизнеса» [Электронный ресурс]: Режим доступа: http://rutube.ru/video/a5f7f1ae8e36ec4fef0a4d94326e3c4d/.
3. Павлов Н. Нестандартные решения в Excel для повседневных задач финансиста [Электронный ресурс]: Электрон. Науч. Жур. «Финансовый директор» №3 — Режим доступа: http://fd.ru/articles/37557
4. Планета Excel. [Электронный ресурс]: Режим доступа: http://www.planetaexcel.ru/
5. Шамшина Н. Использование табличного процессора MS Excel при решении задач на рекурсию // Фізико-математична освіта. Науковий журнал. — Суми : Вид-во СумДПУ ім.А.С.Макаренка, 2013. — № 1 (1). — С. 57-64.
Анотація. Шамшина Н. Методи побудови динамічних діаграм в Excel.
У статті розглянуто методику вивчення динамічних діаграм в табличному процесорі Excel для студентів фізико-математичних спеціальностей педагогічних університетів. Навчання будувати динамічні діаграми пропонується здійснювати за методом детального розгляду практичних прикладів.
Розглянуто питання, які торкаються понять «динамічна діаграма», характерні властивості такого типу візуалізації даних, їх переваги над іншими видами діаграм.
 Описано загальні принципи і методи їх побудови у Excel. Запропоновано приклади для вивчення динамічних діаграм студентами фізико-математичного факультету на лабораторних заняттях з інформатики при вивчення табличного процесора Excel.
Описано загальні принципи і методи їх побудови у Excel. Запропоновано приклади для вивчення динамічних діаграм студентами фізико-математичного факультету на лабораторних заняттях з інформатики при вивчення табличного процесора Excel.Показано, що освоєння методів побудови динамічних діаграм при вивченні табличного процесора не лише готує студентів до майбутньої професійної діяльності, але й підвищує рівень їх інформатичної компетентності, а також сприяє розвитку творчої уяви і активізує пізнавальну діяльність.
Ключові слова: динамічні діаграми, Excel, методика вивчення діаграм.
Аннотация. Шамшина Н. Методы построения динамических диаграмм в
Excel.
В статье рассматривается методика изучения динамических диаграмм в Excel для студентов физико-математических специальностей педагогических
45
PHYSICAL & MATHEMATICAL EDUCATION
№ 1(4), 2015
университетов. Обучение построению динамических диаграмм предлагается осуществлять методом детального рассмотрения практических примеров.
Рассмотрены вопросы, касающиеся понятия «динамическая диаграмма», свойства такого типа визуализации данных, их преимущества, описаны общие принципы и методы их построения в Excel. Предложены примеры для изучения динамических диаграмм студентами физико-математического факультета на лабораторных занятиях по информатике при изучении табличного процессора Excel. Показано, что освоение методов построения динамических диаграмм при изучении табличного процессора Excel не только готовит студентов к профессиональной деятельности, но и повышает уровень их информационной компетентности, а также развивает творческое воображение и активизирует познавательную деятельность.

Ключевые слова: динамические диаграммы, Excel, методика изучения диаграмм.
Abstract. Shamshina N. Methods of construction of dynamic charts in Excel.
The article touches upon method of studying dynamic charts in Excel. It is studies of students of pedagogical universities — future teachers of physics and mathematics. In this Learning to construct of dynamic charts propose to perform a detailed review of the method of practical examples and the issues that concern the concepts of «dynamic chart», the characteristics of this type of visualization, their advantages over other types of diagrams. In article described the general principles and methods of construction charts in Excel.
It is shown that the analiz and development of methods for building dynamic charts in the study of spreadsheet not only prepares students for future careers, but also increases their information competence and promotes of creative imagination and cognitive activity.
Keywords: dynamic charts, Excel, the technique of studying.
46
Статистика: Сила из данных! Типы графиков: гистограммы и гистограммы
Архивный контент
Информация, помеченная как архивная, предназначена для справочных, исследовательских или учетных целей. Он не регулируется веб-стандартами правительства Канады и не изменялся и не обновлялся с момента его архивирования. Свяжитесь с нами, чтобы запросить формат, отличный от доступных.
Гистограмма — популярный инструмент построения графиков. Он используется для суммирования дискретных или непрерывных данных, измеренных в интервальной шкале.Его часто используют для иллюстрации основных особенностей распределения данных в удобной форме.
 Гистограмма делит диапазон возможных значений в наборе данных на классы или группы. Для каждой группы создается прямоугольник с базовой длиной, равной диапазону значений в этой конкретной группе, и площадью, пропорциональной количеству наблюдений, попадающих в эту группу. Это означает, что прямоугольники будут нарисованы неодинаковой высоты. Гистограмма выглядит как вертикальная гистограмма, но когда переменные непрерывны, между столбцами нет промежутков.Однако, когда переменные дискретны, между полосами следует оставлять промежутки. Рисунок 1 — хороший пример гистограммы.
Гистограмма делит диапазон возможных значений в наборе данных на классы или группы. Для каждой группы создается прямоугольник с базовой длиной, равной диапазону значений в этой конкретной группе, и площадью, пропорциональной количеству наблюдений, попадающих в эту группу. Это означает, что прямоугольники будут нарисованы неодинаковой высоты. Гистограмма выглядит как вертикальная гистограмма, но когда переменные непрерывны, между столбцами нет промежутков.Однако, когда переменные дискретны, между полосами следует оставлять промежутки. Рисунок 1 — хороший пример гистограммы.Вертикальная гистограмма и гистограмма различаются следующим образом:
- На гистограмме частота измеряется областью столбца.
- На вертикальной гистограмме частота измеряется высотой полосы.
Характеристики гистограммы
Обычно гистограмма имеет столбцы одинаковой ширины, хотя это не тот случай, когда интервалы классов различаются по размеру.Выбор подходящей ширины полосок для гистограммы очень важен. Как вы можете видеть в приведенном выше примере, гистограмма состоит просто из набора вертикальных полос. Значения изучаемой переменной измеряются в арифметической шкале по горизонтальной оси абсцисс. Полосы имеют одинаковую ширину и соответствуют равным интервалам классов, а высота каждой полоски соответствует частоте класса, который она представляет.
Гистограмма используется для переменных, значения которых являются числовыми и измеряются в интервальной шкале.Обычно он используется при работе с большими наборами данных (более 100 наблюдений). Гистограмма также может помочь обнаружить любые необычные наблюдения (выбросы) или любые пробелы в данных.
Гистограммы
Гистограмма или многоугольник частот — это граф, образованный соединением средних точек вершин столбцов гистограммы. Эти графики используются только при отображении данных из непрерывных переменных, показанных на гистограмме.

Гистограмма сглаживает резкие изменения, которые могут появиться на гистограмме, и полезна для демонстрации непрерывности изучаемой переменной.Рисунки 2 и 3 являются хорошими примерами гистограмм.
В отличие от рисунка 2, на этой гистограмме есть промежутки между полосами. Просто взглянув на эту иллюстрацию, читатель может сразу сказать, что пробелы означают, что переменные дискретны. Таким образом, гистограммы помогают читателям определить, какой тип переменных использовался.
примеров, типов и способов построения гистограмм
Что такое гистограмма?
Гистограмма используется для суммирования дискретных или непрерывных данных.Другими словами, он обеспечивает визуальную интерпретацию данных. Представление данных Аналитики передают результаты финансового анализа руководству, инвесторам и деловым партнерам. Это требует сосредоточения внимания на основных моментах, фактах числовых данных, показывая количество точек данных, которые попадают в указанный диапазон значений (называемый «ячейками»). Он похож на вертикальную гистограмму. Однако гистограмма, в отличие от вертикальной гистограммы, не показывает промежутков между столбцами.
Части гистограммы
- Заголовок: Заголовок описывает информацию, содержащуюся в гистограмме.
- Ось X: Ось X — это интервалы, показывающие шкалу значений, под которую попадают измерения.
- Ось Y: Ось Y показывает, сколько раз значения встречались в пределах интервалов, установленных осью X.
- Полосы: Высота полосы показывает, сколько раз значения встречались в пределах интервала, а ширина полосы показывает покрытый интервал. Для гистограммы с одинаковыми ячейками ширина должна быть одинаковой для всех столбцов.
Важность гистограммы
Создание гистограммы обеспечивает визуальное представление распределения данных.
 Гистограммы могут отображать большой объем данных и функцию частоты. Функция частоты. Функция частоты относится к категории статистических функций Excel. Функция рассчитает и вернет частотное распределение. Мы можем использовать его, чтобы получить частоту значений в наборе данных. значений данных. Функция medianMEDIAN Функция MEDIAN относится к категории Статистических функций Excel.Функция вычислит среднее значение заданного набора чисел. Медиана может быть определена как среднее число группы чисел. То есть половина чисел возвращает значения, которые больше медианы, и распределение данных можно определить с помощью гистограммы. Кроме того, он может отображать любые выбросы или пробелы в данных.
Гистограммы могут отображать большой объем данных и функцию частоты. Функция частоты. Функция частоты относится к категории статистических функций Excel. Функция рассчитает и вернет частотное распределение. Мы можем использовать его, чтобы получить частоту значений в наборе данных. значений данных. Функция medianMEDIAN Функция MEDIAN относится к категории Статистических функций Excel.Функция вычислит среднее значение заданного набора чисел. Медиана может быть определена как среднее число группы чисел. То есть половина чисел возвращает значения, которые больше медианы, и распределение данных можно определить с помощью гистограммы. Кроме того, он может отображать любые выбросы или пробелы в данных.Распределения гистограммы
Нормальное распределение: В нормальном распределении точки на одной стороне от среднего Функция AVERAGE Расчет среднего значения в Excel.Функция СРЕДНИЙ относится к Статистическим функциям. Он вернет среднее значение аргументов. Он используется для вычисления среднего арифметического заданного набора аргументов. Финансовому аналитику эта функция полезна для определения среднего числа. с такой же вероятностью, как и на другой стороне среднего.
Бимодальное распределение: В бимодальном распределении есть два пика. При бимодальном распределении данные следует разделять и анализировать как отдельные нормальные распределения.
Распределение со смещением вправо: Распределение со смещением вправо также называется положительно наклонным распределением. В распределении со смещением вправо большое количество значений данных находится в левой части с меньшим количеством значений данных в правой части. Распределение с перекосом вправо обычно возникает, когда данные имеют границу диапазона в левой части гистограммы. Например, граница 0.
Скошенное влево распределение: Скошенное влево распределение также называется отрицательно скошенным распределением.
 В распределении со смещением влево большое количество значений данных находится в правой части, а меньшее количество значений данных — в левой. Распределение с перекосом вправо обычно возникает, когда данные имеют границу диапазона в правой части гистограммы. Например, граница, такая как 100.
В распределении со смещением влево большое количество значений данных находится в правой части, а меньшее количество значений данных — в левой. Распределение с перекосом вправо обычно возникает, когда данные имеют границу диапазона в правой части гистограммы. Например, граница, такая как 100.Случайное распределение: Случайное распределение не имеет очевидной закономерности и имеет несколько пиков. В гистограмме случайного распределения может быть случай, когда были объединены разные свойства данных.Поэтому данные следует разделять и анализировать отдельно.
Пример гистограммы
Джефф — менеджер филиала в местном банке. Недавно Джефф получил отзывы клиентов, в которых говорилось, что время ожидания обслуживания клиента представителем службы поддержки слишком велико. Джефф решает наблюдать и записывать время, потраченное каждым клиентом на ожидание. Вот его результаты наблюдения и записи времени ожидания, потраченного 20 клиентами:
Соответствующая гистограмма с 5-секундными ячейками (5-секундные интервалы) будет выглядеть следующим образом:
Мы видим, что:
- Есть 3 клиента ожидают между 1 и 35 секунд
- Есть 5 клиентов ожидают между 1 и 40 секундами
- Есть 5 клиентов ожидают между 1 и 45 секунд
- Есть 5 клиентов ожидают между 1 и 50 секундами
- Есть 2 клиента ожидают между 1 и 55 секундами
Джефф может сделать вывод, что большинство клиентов ждут между 35.1 и 50 секунд.
Как создать гистограмму
Давайте создадим нашу собственную гистограмму. Загрузите соответствующий файл шаблона Excel для этого примера.

Шаг 1: Откройте окно анализа данных. Это можно найти на вкладке Данные как Анализ данных :
Шаг 2: Выберите Гистограмма :
Шаг 3: Введите соответствующий диапазон ввода и диапазон бункера.В этом примере диапазоны должны быть:
- Диапазон ввода: $ C $ 10: $ D $ 19
- Диапазон ячеек: $ F $ 9: $ F $ 24
Убедитесь, что «Вывод диаграммы» отмечен и нажмите «ОК».
Загрузите пример шаблона, чтобы создать его самостоятельно!
Ссылки по теме
CFI является официальным поставщиком глобальной сертификации финансового моделирования и оценки (FMVA) ™ FMVA® Certification Присоединяйтесь к более 850 000 студентов, которые работают в таких компаниях, как Amazon, J.П. Морган и программа сертификации Ferrari, призванная помочь любому стать финансовым аналитиком мирового уровня. Чтобы продолжить продвижение по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI:
- Типы графиков в Excel Типы графиков 10 типов графиков для представления данных, которые вы должны использовать — примеры, советы, форматирование, как использовать эти различные графики для эффективного общение и в презентациях. Загрузите шаблон Excel с линейчатой диаграммой, линейной диаграммой, круговой диаграммой, гистограммой, водопадом, диаграммой рассеяния, комбинированной диаграммой (столбик и линия), измерительной диаграммой,
- Создание информационной панели в Excel Создание информационной панели в ExcelЭто руководство по созданию приборной панели в Excel научит вас, как построить красивую дашборд в Excel, используя приемы визуализации данных от профессионалов.В
- Ярлыки Excel Ярлыки ПК и MacExcel Ярлыки MacExcel для ПК — список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета.
 Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения.
Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения. - Список функций Excel ФункцииСписок наиболее важных функций Excel для финансовых аналитиков.Эта шпаргалка охватывает 100 функций, которые критически важно знать аналитику Excel.
Гистограмма — краткое введение
сообщить об этом объявлении Рубен Герт ван ден Берг в разделе «Диаграммы и статистика» от А до ЯГистограмма — это диаграмма, показывающая частоты для
интервалов значений метрической переменной. Такие интервалы называются «ячейками», и все они имеют одинаковую ширину. В приведенном выше примере ширина корзины составляет 25 долларов. Таким образом, он показывает, сколько людей зарабатывают от 800 до 825 долларов, от 825 до 850 долларов и так далее.
Обратите внимание, что режим этого частотного распределения составляет от 900 до 925 долларов, что встречается примерно 150 раз.Гистограмма — пример
Компания хочет знать, как ежемесячная заработная плата распределяется между 1110 сотрудниками, имеющими рабочие места на уровне оперативного, среднего или высшего руководства. На скриншоте ниже показано, как выглядят их необработанные данные.
Поскольку эти зарплаты частично основаны на комиссионных, в основном у каждого сотрудника немного разная зарплата. Теперь, как мы можем получить представление о распределении заработной платы?
Гистограммаи столбчатая диаграмма
Сначала мы пробуем построить гистограмму месячных зарплат.Результат показан ниже.
Наша гистограмма бесполезна. Единственное, что мы извлекаем из этого, это то, что большинство зарплат выплачиваются только один раз, а некоторые — дважды. Основная проблема здесь в том, что гистограмма показывает частоту , с которой каждое отдельное значение встречается в данных .

Важно отметить, что первый интервал имеет ширину (832 доллара — 802 доллара =) 30 долларов. Последний интервал представляет (1206 — 1119 долларов =) 87 долларов. Но оба имеют одинаковую ширину в миллиметрах на вашем экране. Это говорит нам о том, что ось x не имеет линейного масштаба что делает эту диаграмму непригодной для такой метрической переменной, как ежемесячная зарплата.Гистограмма — базовый пример
Поскольку наша гистограмма не очень хороша, мы теперь пытаемся запустить гистограмму на наших данных. Результат показан ниже.
Эта диаграмма выглядит намного полезнее, но как она была создана? Итак, мы распределили зарплату каждого сотрудника с интервалом в 25 долларов (800-825 долларов, 825-850 долларов и так далее). Затем мы посмотрели количество сотрудников, попадающих в каждый такой интервал. Мы визуализируем эти частоты в виде столбцов на графике.
Важно отметить, что ось нашей диаграммы имеет линейный масштаб : каждый интервал в 25 долларов соответствует той же ширине в миллиметрах, даже если он не содержит сотрудников.График, который мы получили, известен как гистограмма, и, как мы увидим через минуту, она очень полезна.Гистограмма — ширина ячейки
Ширина бина — это ширина интервалов
, частоты которых мы визуализируем на гистограмме. В нашем первом примере использовалась корзина шириной 25 долларов; первая полоса представляет собой количество зарплат от 800 до 825 долларов и так далее. Эта ширина ячейки в 25 долларов — это скорее , произвольный выбор . На рисунке ниже показаны гистограммы для одних и тех же данных с использованием разной ширины бинов.Хотя разная ширина бинов кажется разумной, мы считаем, что 10 долларов — это довольно мало, а 100 долларов — довольно много для имеющихся данных. Кажется, больше подходят 25 или 50 долларов.
Гистограммы — почему они так полезны?
Почему гистограммы так полезны? Во-первых, диаграммы намного нагляднее, чем таблицы; посмотрев на диаграмму в течение 10 секунд, вы сможете узнать о своих данных гораздо больше, чем после 10 секунд просмотра соответствующей таблицы.
 Как правило, диаграммы передают информацию о наших данных быстрее, чем таблицы , хотя и менее точно.
Как правило, диаграммы передают информацию о наших данных быстрее, чем таблицы , хотя и менее точно.
Вдобавок к этому гистограммы также дают нам более более полную информацию о наших данных. Помните, что вы можете разумно оценить среднее значение переменной, стандартное отклонение, асимметрию и эксцесс по гистограмме. Однако вы не можете оценить гистограмму переменной на основе вышеупомянутой статистики. Проиллюстрируем это на примере.Гистограмма и описательная статистика
Допустим, мы находим в наших данных две возрастные переменные и не уверены, какую из них следует использовать.Мы сравниваем базовую описательную статистику для обеих переменных, и они выглядят почти одинаково.
Итак, можем ли мы сделать вывод, что обе возрастные переменные имеют примерно одинаковое распределение? Если вы так думаете, взгляните на их гистограммы, показанные ниже.
Разделенная гистограмма — частоты
Каждый из 1110 сотрудников в наших данных имеет уровень должности: операционный, средний менеджмент или высшее руководство. Если мы хотим сравнить распределение заработной платы между этими тремя группами, мы можем проверить разделенную гистограмму: мы создаем отдельную гистограмму для каждого уровня должности, и эти три гистограммы имеют идентичных осей .Результат показан ниже.
Наша разделенная гистограмма — отстой. Проблема в том, что размеры групп очень неравны, и они линейно связаны с площадями поверхности наших гистограмм. В результате площадь для высшего руководства (n = 10) составляет только 1% от площади для «оперативного» (n = 1000). Гистограмма для высшего руководства настолько мала, что ее больше не видно.
Разделенная гистограмма — проценты
Мы только что видели, что разделенная гистограмма с частотами бесполезна для имеющихся данных.Означает ли это, что мы не можем сравнивать распределение заработной платы по уровням должностей? Неа.
 Если мы выберем процентное соотношение внутри групп уровня должностей, то каждая гистограмма будет иметь одинаковую площадь поверхности 100%. Результат показан ниже.
Если мы выберем процентное соотношение внутри групп уровня должностей, то каждая гистограмма будет иметь одинаковую площадь поверхности 100%. Результат показан ниже.Гистограмма — Заключительные примечания
Этот учебник был направлен на объяснение того, что такое гистограммы и чем они отличаются от гистограмм. На наш взгляд, гистограммы — одни из самых полезных диаграмм для метрических переменных. С помощью подходящего программного обеспечения (такого как SPSS) вы можете очень быстро создавать и проверять гистограммы, и это отличный способ познакомиться с вашими данными.
Гистограмма и их использование
Гистограмма очень похожа на гистограммы. Эта диаграмма представляет собой комбинацию линейной диаграммы и вертикальной гистограммы. Данные здесь отображаются с помощью прямоугольников одинакового размера. Гистограмма используется для отображения распределения информации или данных за непрерывный период времени. Площадь прямоугольных полос пропорциональна частоте переменной.
Гистограммы могут иметь внешний вид, похожий на гистограммы, но, в отличие от них, используются для отображения частоты появления переменных в непрерывных данных.Эти непрерывные данные разделены на классы, называемые корзинами. С помощью этих ящиков можно легко определить точки большинства и меньшинства. Кроме того, при рисовании гистограммы следует убедиться, что ячейки не будут слишком тонкими, что может повлиять на поток частотного распределения, или слишком толстыми, что затруднит просмотр изменений в данных.
Давайте возьмем пример с клиентами, ожидающими в банке.
Источник изображения: гистограмма
Приведенная выше таблица дает нам данные опроса клиентов, проведенного банком, об их соответствующем времени ожидания.Этот лист данных построен в виде гистограммы с 5-секундными интервалами. Полученный график проиллюстрирован ниже.
Источник изображения: Гистограмма исследования
Мы можем очень хорошо сказать из этого графика, что клиенты ждали от 35 до 50 секунд.
 Как видите, гистограммы непрерывны и не имеют пропусков, однако, если для определенной точки нет значения частоты, могут возникать пропуски. Эти пробелы можно легко обнаружить и они служат еще одним преимуществом гистограммы.
Как видите, гистограммы непрерывны и не имеют пропусков, однако, если для определенной точки нет значения частоты, могут возникать пропуски. Эти пробелы можно легко обнаружить и они служат еще одним преимуществом гистограммы.В базовом типе гистограммы независимая переменная отображается по оси x, а зависимая переменная отображается по оси y. Прямоугольные полосы окрашены или заштрихованы для обозначения различных категорий. Давайте посмотрим на то же самое. Предположим, учитель анализирует итоговые экзаменационные оценки своих учеников. Каждый диапазон отметок обозначен другим цветом.
Источник изображения: гистограмма
С помощью этой гистограммы можно получить несколько результатов, касающихся обучающих способностей учителя и интеллекта ученика.
Гистограммы полезны не только для определения минимальной точки данных, максимальной точки данных и медианы. Но он также используется для определения стандартной медианы данных. Диапазон диаграммы слева направо, который также называется шириной класса диаграммы, можно определить с помощью гистограммы.
Распределение гистограмм
Существует множество способов распределения гистограммы. Вот несколько типов дистрибутивов, которые мы рассмотрим.
- Нормальное распределение
- Бимодальное распределение
- Распределение скошенное вправо
- Распределение с перекосом влево
- Равномерное распределение
- Случайное распределение
В этом типе распределения данных гистограмма образует перевернутую V-образную фигуру.Точки данных, встречающиеся на одной стороне, аналогичны тем, которые встречаются на другой стороне. Иллюстрация этой колоколообразной или ступенчатой конструкции с одним пиком приводится ниже.
Источник изображения: нормальное распределение гистограммы
Бимодальное распределение гистограммыЭтот тип распределения гистограмм состоит из двух нормальных типов распределения.
 Это указывает на то, что данные собираются из двух разных систем. В случае возникновения такого распределения данные должны быть проанализированы отдельно для обоих пиков.
Это указывает на то, что данные собираются из двух разных систем. В случае возникновения такого распределения данные должны быть проанализированы отдельно для обоих пиков.Источник изображения: бимодальное распределение гистограммы
Распределение гистограммы, скошенное вправоВ этом типе распределения гистограмм большие значения встречаются слева, чем справа, что делает график наклонным вправо. Этот тип графа также называется положительно скошенным распределением.
Источник: правостороннее распределение гистограммы
Распределение гистограммы с перекосом влевоГистограмма этого типа наклонена влево.В отличие от распределения со смещением вправо, здесь большие значения данных встречаются с правой стороны, чем с левой стороны. Этот тип распределения гистограммы также называется распределением с отрицательным перекосом.
Источник изображения: скошенное влево распределение гистограммы
Случайное распределение гистограммыКак следует из названия, распределение этой гистограммы случайное, и здесь видно множество пиков. Учитывая форму графика, можно сказать, что данные были собраны из разных источников или разных групп.Этот тип графа обычно встречается при наличии нескольких систем.
Источник изображения: случайное распределение гистограммы
Равномерное распределение гистограммыВ этом типе распределения гистограмм все пики оказываются почти одинакового размера, что дает мало информации об источнике. Если такой узор сформирован, это может быть связано с меньшим количеством систем.
Источник изображения: Равномерное распределение гистограммы
Плюсы гистограммы- Гистограммы помогают графически отображать большие объемы данных, которые трудно преобразовать в табличную форму.
- Это упрощает отображение данных различных типов и частот.

- Это полезно для визуализации распределения данных.
- С помощью гистограммы можно определить медианное значение, распределение и вариации данных.
- Гистограмма сообщает нам об асимметрии нанесенных данных.
- Эти диаграммы также помогают прогнозировать будущую производительность процесса.
- Это упрощает расчет возможностей процесса.
- Гистограммы очень согласованы, так как интервалы равномерно распределены,
- Таблицы данных можно легко преобразовать в гистограммы.
- Гистограммы полезны при вычислении стандартного отклонения данных.
- Диапазон диаграммы можно найти с помощью этого графика.
- Гистограммы относятся к числу удобных для чтения диаграмм. Легко читать и понимать.
- Гистограммы часто строятся для помощи в принятии решений.
- Эти графики подходят для использования, когда доступные данные находятся в очень большом диапазоне.Например, при опросе студентов колледжа, припарковывающих автомобили за пределами кампуса.
- При построении гистограммы можно использовать только непрерывные данные.
- Эта форма диаграммы не очень подходит для сравнения двух типов данных.
- Точное значение данных не используется для построения графика, так как данные всегда группируются или классифицируются.
- Если не нанесено частотное распределение, точные данные гистограммы не могут быть извлечены из графика.
- Гистограммы — это диаграммы, которыми можно легко управлять для достижения желаемого результата.
- Иногда при построении гистограммы разницей во времени данных пренебрегают.
- Они очень неудобны при сравнении множества разных категорий данных вместе.
Это были некоторые факты о гистограммах и их функциях. Надеюсь, это помогло вам понять, какие данные подходят для построения гистограммы.
Полное руководство по гистограммам
Что такое гистограмма?
Гистограмма — это диаграмма, на которой показано распределение значений числовой переменной в виде серии столбцов.
 Каждая полоса обычно охватывает диапазон числовых значений, называемых ячейкой или классом; высота столбца указывает частоту точек данных со значением в соответствующем интервале.
Каждая полоса обычно охватывает диапазон числовых значений, называемых ячейкой или классом; высота столбца указывает частоту точек данных со значением в соответствующем интервале.Гистограмма выше показывает частотное распределение времени до ответа на билеты, отправленные в вымышленную систему поддержки. Каждая полоса охватывает один час времени, а высота указывает количество билетов в каждом временном диапазоне. Мы можем видеть, что наибольшая частота ответов была в диапазоне 2-3 часов, с более длинным хвостом справа, чем слева.Есть также холм поменьше, пик (режим) которого находится в диапазоне 13-14 часов. Если бы мы смотрели только на числовую статистику, такую как среднее значение и стандартное отклонение, мы могли бы упустить тот факт, что эти два пика способствовали общей статистике.
Когда следует использовать гистограмму
Гистограммы хороши для демонстрации общих особенностей распределения переменных набора данных. Вы можете примерно увидеть, где находятся пики распределения, является ли распределение асимметричным или асимметричным, и есть ли какие-либо выбросы.
Чтобы использовать гистограмму, нам просто нужна переменная, которая принимает непрерывные числовые значения. Это означает, что различия между значениями постоянны независимо от их абсолютных значений. Например, даже если оценка за тест может принимать только целые числа от 0 до 100, пробел одинакового размера имеет одинаковое значение независимо от того, где мы находимся на шкале: разница между 60 и 65 — это те же 5 баллов. размер как разница между 90 и 95.
Информация о количестве бинов и их границах для подсчета точек данных не присуща самим данным.Вместо этого настройка интервалов — это отдельное решение, которое мы должны принять при построении гистограммы. Способ, которым мы указываем интервалы, будет иметь большое влияние на то, как можно интерпретировать гистограмму, как будет показано ниже.
Когда значение находится на границе ячейки, оно будет последовательно назначаться ячейке справа или слева (или конечным ячейкам, если оно находится в конечных точках).
 Какая сторона будет выбрана, зависит от инструмента визуализации; у некоторых инструментов есть возможность переопределить их настройки по умолчанию.В этой статье предполагается, что значения на границе ячейки будут присвоены ячейке справа.
Какая сторона будет выбрана, зависит от инструмента визуализации; у некоторых инструментов есть возможность переопределить их настройки по умолчанию.В этой статье предполагается, что значения на границе ячейки будут присвоены ячейке справа.Пример структуры данных
Один из способов работы инструментов визуализации с данными, которые должны быть визуализированы в виде гистограммы, — это использование обобщенной формы, подобной приведенной выше. Здесь первый столбец указывает границы интервала, а второй — количество наблюдений в каждом интервале. В качестве альтернативы некоторые инструменты могут просто работать с исходным неагрегированным столбцом данных, а затем применять к данным указанные параметры разделения при создании гистограммы.
Рекомендации по использованию гистограммы
Используйте нулевой базовый показатель
Важным аспектом гистограмм является то, что они должны быть построены с нулевым значением базовой линии. Поскольку частота данных в каждой ячейке подразумевается высотой каждой полосы, изменение базовой линии или введение разрыва в шкале исказит восприятие распределения данных.
Если отсечь 80 баллов от вертикальной оси, распределение оценок производительности будет выглядеть намного лучше, чем есть на самом деле.Выберите подходящее количество ящиков
Хотя инструменты, которые могут генерировать гистограммы, обычно имеют некоторые алгоритмы по умолчанию для выбора границ интервалов, вы, вероятно, захотите поиграть с параметрами интервалов, чтобы выбрать что-то, что является репрезентативным для ваших данных. В Википедии есть обширный раздел, посвященный практическим правилам выбора подходящего количества ящиков и их размеров, но в конечном итоге стоит использовать знания предметной области, а также изрядно поиграть с различными вариантами, чтобы узнать, что лучше всего подойдет для ваших целей.
Выбор размера ящика имеет обратную зависимость от количества ячеек.
Бункеры на левой панели слишком малы, что подразумевает множество ложных пиков и впадин. Бункеры на правой панели слишком велики, что скрывает любые признаки второго пика. Чем больше размер ячеек, тем меньше ячеек будет для охвата всего диапазона данных. Чем меньше размер бункера, тем больше должно быть бункеров. Стоит потратить некоторое время на то, чтобы протестировать различные размеры бункеров, чтобы увидеть, как распределение выглядит в каждом из них, а затем выбрать график, который лучше всего представляет данные. Если у вас слишком много бинов, тогда распределение данных будет выглядеть грубым, и будет сложно отличить сигнал от шума.С другой стороны, при слишком малом количестве интервалов гистограмме будет не хватать деталей, необходимых для различения любого полезного паттерна из данных.
Чем больше размер ячеек, тем меньше ячеек будет для охвата всего диапазона данных. Чем меньше размер бункера, тем больше должно быть бункеров. Стоит потратить некоторое время на то, чтобы протестировать различные размеры бункеров, чтобы увидеть, как распределение выглядит в каждом из них, а затем выбрать график, который лучше всего представляет данные. Если у вас слишком много бинов, тогда распределение данных будет выглядеть грубым, и будет сложно отличить сигнал от шума.С другой стороны, при слишком малом количестве интервалов гистограмме будет не хватать деталей, необходимых для различения любого полезного паттерна из данных.Выберите интерпретируемые границы ячеек
Деления и метки обычно должны попадать на границы ячейки, чтобы лучше информировать, где находятся пределы каждой полосы. Ярлыки не нужно устанавливать для каждой полосы, но их размещение между каждыми несколькими полосами помогает читателю отслеживать ценность.Кроме того, полезно, если метки представляют собой значения с небольшим количеством значащих цифр, чтобы их было удобно читать.
Это говорит о том, что ячейки размером 1, 2, 2,5, 4 или 5 (которые делят 5, 10 и 20 поровну) или их степень десяти являются хорошими размерами ячеек для начала в качестве практического правила. Это также означает, что ячейки размером 3, 7 или 9, вероятно, будет труднее читать, и их не следует использовать, если контекст не имеет для них смысла.
Вверху: небрежное разделение данных на десять ячеек от минимального до максимального может закончиться очень странным разделением ячеек.Внизу: требуется меньше делений, если размер корзины легко проследить.Небольшое предостережение: убедитесь, что вы учитываете типы значений, которые принимает интересующая вас переменная. В случае дробного размера ячейки, например 2,5, это может быть проблемой, если ваша переменная принимает только целые значения.
На рисунке выше показано распределение результатов при суммировании результатов пяти бросков кубика, повторенных 20 000 раз. Ожидаемая форма колокольчика выглядит остроконечной или однобокой, когда выбираются размеры бункера, которые отражают разное количество целочисленных результатов. Бин от 0 до 2,5 имеет возможность собирать три разных значения (0, 1, 2), но следующий интервал от 2,5 до 5 может собирать только два разных значения (3, 4-5 попадут в следующий интервал).Это означает, что ваша гистограмма может выглядеть неестественно «неровной» просто из-за количества значений, которые может принимать каждая ячейка.
Бин от 0 до 2,5 имеет возможность собирать три разных значения (0, 1, 2), но следующий интервал от 2,5 до 5 может собирать только два разных значения (3, 4-5 попадут в следующий интервал).Это означает, что ваша гистограмма может выглядеть неестественно «неровной» просто из-за количества значений, которые может принимать каждая ячейка.Распространенные ошибки
Измеряемая переменная не является непрерывной числовой
Как отмечалось в начальных разделах, гистограмма предназначена для изображения частотного распределения непрерывной числовой переменной.Когда интересующая нас переменная не соответствует этому свойству, нам нужно вместо этого использовать другой тип диаграммы: гистограмму. Переменные, которые принимают категориальные значения, такие как тип пользователя (например, гость, пользователь) или местоположение, явно не являются числовыми, поэтому должны использовать гистограмму. Однако есть определенные типы переменных, которые может быть сложнее классифицировать: те, которые принимают дискретные числовые значения, и те, которые принимают значения, основанные на времени.
Переменные, которые принимают дискретные числовые значения (например, целые числа 1, 2, 3 и т. Д.) можно построить с помощью гистограммы или гистограммы, в зависимости от контекста. Использование гистограммы будет более вероятно, когда есть много разных значений для построения. Когда диапазон числовых значений велик, тот факт, что значения являются дискретными, обычно не имеет значения, и непрерывное группирование будет хорошей идеей.
Одна важная вещь, о которой следует помнить, — это то, что числа представляют фактическую ценность. Если числа на самом деле являются кодами категориальной или слабо упорядоченной переменной, то это признак того, что следует использовать гистограмму.
 Например, если у вас есть ответы на опрос по шкале от 1 до 5, значения кодирования от «категорически не согласен» до «полностью согласен», то частотное распределение должно быть визуализировано в виде гистограммы. Причина в том, что различия между отдельными ценностями могут быть непоследовательными: мы действительно не знаем, что значимая разница между 1 и 2 («категорически не согласен» — «не согласен») такая же, как разница между 2 и 3. («Не согласен» — «ни согласен, ни не согласен»).
Например, если у вас есть ответы на опрос по шкале от 1 до 5, значения кодирования от «категорически не согласен» до «полностью согласен», то частотное распределение должно быть визуализировано в виде гистограммы. Причина в том, что различия между отдельными ценностями могут быть непоследовательными: мы действительно не знаем, что значимая разница между 1 и 2 («категорически не согласен» — «не согласен») такая же, как разница между 2 и 3. («Не согласен» — «ни согласен, ни не согласен»).Более сложный случай — это когда интересующая нас переменная зависит от времени.Когда значения соответствуют относительным периодам времени (например, 30 секунд, 20 минут), тогда имеет смысл разбиение по периодам времени для гистограммы. Однако, когда значения соответствуют абсолютному времени (например, 10 января, 12:15), различие становится размытым. Когда записываются новые точки данных, значения обычно попадают во вновь созданные ячейки, а не в существующий диапазон ячеек. Кроме того, некоторые варианты естественной группировки, например по месяцам или кварталам, приводят к несколько неравным размерам ячеек. По этим причинам нет ничего необычного в использовании другого типа диаграммы, например гистограммы или линейной диаграммы.
Использование бункеров разного размера
Хотя до сих пор во всех примерах гистограммы были показаны с использованием интервалов одинакового размера, на самом деле это не является техническим требованием. Когда данных мало, например, когда есть длинный хвост данных, может прийти в голову идея использовать бункеры большей ширины, чтобы покрыть это пространство. Однако создание гистограммы с ячейками неравного размера не является строго ошибкой, но для этого требуются некоторые серьезные изменения в том, как создается гистограмма, и это может вызвать множество трудностей при интерпретации.
Техническая особенность гистограмм заключается в том, что общая площадь полосок представляет собой целое, а площадь, занимаемая каждой полосой, представляет собой долю целого, содержащегося в каждой ячейке.
Слева: гистограмма с ячейками одинакового размера; В центре: гистограмма с неравными интервалами, но неправильными единицами измерения по вертикальной оси; Справа: гистограмма с неравными ячейками с высотой плотности Когда размеры бункера совпадают, это делает измерение площади стержня и высоты эквивалентным. Однако в гистограмме с переменными размерами ячеек высота больше не может соответствовать общей частоте появления. Это исказит представление о том, сколько точек находится в каждой ячейке, поскольку увеличение размера ячейки только увеличивает ее размер.На центральном графике рисунка ниже интервалы 5-6, 6-7 и 7-10 выглядят так, как будто они содержат больше точек, чем на самом деле.
Когда размеры бункера совпадают, это делает измерение площади стержня и высоты эквивалентным. Однако в гистограмме с переменными размерами ячеек высота больше не может соответствовать общей частоте появления. Это исказит представление о том, сколько точек находится в каждой ячейке, поскольку увеличение размера ячейки только увеличивает ее размер.На центральном графике рисунка ниже интервалы 5-6, 6-7 и 7-10 выглядят так, как будто они содержат больше точек, чем на самом деле.Вместо этого по вертикальной оси необходимо кодировать частоту , плотность на единицу размера ячейки. Например, на правой панели приведенного выше рисунка корзина от 2 до 2,5 имеет высоту около 0.32. Умножьте на ширину бина 0,5, и мы сможем оценить около 16% данных в этом бункере. Высота более широких интервалов была уменьшена по сравнению с центральной панелью: обратите внимание, как общая форма выглядит похожей на исходную гистограмму с одинаковыми размерами интервалов. Плотность — нелегкая концепция для понимания, и такой сюжет, представленный другим, незнакомым с концепцией, будет трудно интерпретировать его.
Из-за всего этого лучший совет — попробовать и просто придерживаться полностью одинаковых размеров бункеров.Наличие пустых интервалов и некоторого повышенного шума в диапазонах с разреженными данными обычно стоит повышения интерпретируемости вашей гистограммы. С другой стороны, если есть неотъемлемые аспекты переменной, которые должны быть нанесены на график, которые предполагают неравные размеры ячеек, то вместо использования гистограммы с неравномерными ячейками вам может быть лучше использовать гистограмму.
Общие параметры гистограммы
Абсолютная частота в зависимости от относительной частоты
В зависимости от целей вашей визуализации вы можете захотеть изменить единицы на вертикальной оси графика как абсолютную частоту или относительную частоту.
Преобразуя первый пример в относительную частоту, гораздо проще сложить первые пять полосок и обнаружить, что примерно на половину заявок отвечает в течение пяти часов. Абсолютная частота — это просто естественное количество появлений в каждом интервале, а относительная частота — это пропорция появлений в каждом интервале. Выбор единиц оси будет зависеть от того, какие виды сравнений вы хотите выделить при распределении данных.
Абсолютная частота — это просто естественное количество появлений в каждом интервале, а относительная частота — это пропорция появлений в каждом интервале. Выбор единиц оси будет зависеть от того, какие виды сравнений вы хотите выделить при распределении данных.Отображение неизвестных или отсутствующих данных
На самом деле это , а не , особенно распространенный вариант, но его стоит рассмотреть, когда дело доходит до настройки ваших графиков.Если в строке данных отсутствует значение интересующей переменной, оно часто пропускается в подсчете для каждой ячейки. Если важно показать количество пропущенных или неизвестных значений, вы можете объединить гистограмму с дополнительной полосой, которая отображает частоту этих неизвестных. При построении этого столбца рекомендуется поместить его на параллельную ось от основной гистограммы и другим нейтральным цветом, чтобы точки, собранные на этом столбце, не были перепутаны с числовым значением.
Смежные участки
Гистограмма
Как отмечалось выше, если интересующая нас переменная не является непрерывной и числовой, а дискретна или категориальна, то вместо этого нам понадобится гистограмма. В отличие от гистограммы, столбцы на гистограмме обычно имеют небольшой промежуток между собой: это подчеркивает дискретный характер отображаемой переменной.
Линейный график
Если вы сгруппировали числовые данные, но хотите, чтобы вертикальная ось вашего графика передавала что-то, кроме частотной информации, вам следует обратить внимание на использование линейной диаграммы.Вертикальное положение точек на линейной диаграмме может отображать значения или статистические сводки второй переменной. Когда линейная диаграмма используется для изображения частотных распределений, таких как гистограмма, это называется многоугольником частот .

Кривая плотности
Кривая плотности или оценка плотности ядра (KDE) — это альтернатива гистограмме, которая дает каждой точке данных непрерывный вклад в распределение. На гистограмме вы можете представить себе каждую точку данных как переливание жидкости из ее значения в ряд цилиндров ниже (бункеры).В KDE каждая точка данных добавляет небольшой кусок объема вокруг своего истинного значения, который складывается по точкам данных для создания окончательной кривой. Форма объема — это «ядро», и существует безграничный выбор. Из-за огромного количества опций при выборе ядра и его параметров кривые плотности обычно являются областью программных средств визуализации.
Толстыми черными штрихами обозначены точки данных, которые влияют на гистограмму (слева) и кривую плотности (справа).Обратите внимание, как каждая точка вносит небольшую колоколообразную кривую в общую форму.Коробчатый сюжет и скрипичный сюжет
Гистограммы хорошо показывают распределение одной переменной, но довольно сложно провести сравнение между гистограммами, если мы хотим сравнить эту переменную между разными группами. Одним из возможных решений для двух групп является построение гистограмм двух групп подряд. Специфической для домена версией этого типа графика является пирамида численности населения , которая отображает возрастное распределение страны или другого региона для мужчин и женщин в виде последовательных вертикальных гистограмм.
Однако, если у нас есть три или более групп, последовательное решение не сработает. Одним из решений может быть создание фасетных гистограмм, построение по одной для каждой группы в строке или столбце. Другой альтернативой является использование другого типа сюжета, такого как коробчатый сюжет или сюжет для скрипки. Оба этих типа графиков обычно используются, когда мы хотим сравнить распределение числовой переменной по уровням категориальной переменной. По сравнению с фасетными гистограммами эти графики торгуют точным отображением абсолютной частоты для более компактного относительного сравнения распределений.

Как довольно распространенный тип визуализации, большинство инструментов, способных создавать визуализации, имеют гистограмму в качестве опции. Если гистограмма недоступна, гистограмма должна быть доступна в качестве близкого заменителя. Создание гистограммы может потребовать немного больше работы, чем другие базовые типы диаграмм, из-за необходимости тестирования различных вариантов разбиения, чтобы найти лучший вариант. Однако эти усилия часто того стоят, поскольку хорошая гистограмма может быть очень быстрым способом точной передачи общей формы и распределения переменной данных.
Гистограмма — это один из множества различных типов диаграмм, которые можно использовать для визуализации данных. Узнайте больше из наших статей о основных типах диаграмм, о том, как выбрать тип визуализации данных, или просмотрев полную коллекцию статей в категории диаграмм.
Что такое гистограмма и как ее использовать?
Гистограмма — это тип графика, который имеет широкое применение в статистике. Гистограммы обеспечивают визуальную интерпретацию числовых данных, указывая количество точек данных, лежащих в пределах диапазона значений.Эти диапазоны значений называются классами или ячейками. Частота данных, попадающих в каждый класс, отображается с помощью столбца. Чем выше полоса, тем выше частота значений данных в этой ячейке.
Гистограммы и гистограммы
На первый взгляд гистограммы очень похожи на гистограммы. Оба графика используют вертикальные полосы для представления данных. Высота полосы соответствует относительной частоте количества данных в классе. Чем выше полоса, тем выше частота данных.Чем ниже полоса, тем ниже частота данных. Но внешность обманчива. На этом сходство между двумя видами графов заканчивается.
Причина того, что эти виды графиков различаются, связана с уровнем измерения данных. С одной стороны, гистограммы используются для данных на номинальном уровне измерения. Гистограммы измеряют частоту категориальных данных, и классы для гистограммы являются этими категориями.
 С другой стороны, гистограммы используются для данных, которые находятся, по крайней мере, на порядковом уровне измерения.Классы гистограммы — это диапазоны значений.
С другой стороны, гистограммы используются для данных, которые находятся, по крайней мере, на порядковом уровне измерения.Классы гистограммы — это диапазоны значений.Еще одно ключевое различие между гистограммами и гистограммами связано с порядком столбцов. На гистограмме принято менять расположение полос в порядке убывания высоты. Однако столбцы на гистограмме не могут быть переставлены. Они должны отображаться в том порядке, в котором происходят классы.
Пример гистограммы
Диаграмма выше показывает нам гистограмму. Предположим, что четыре монеты подброшены и результаты записаны.Использование соответствующей таблицы биномиального распределения или простых вычислений с помощью биномиальной формулы показывает, что вероятность того, что ни одна голова не отображается, равна 1/16, вероятность того, что одна голова отображается, равна 4/16. Вероятность выпадения двух орлов — 6/16. Вероятность выпадения трех решек — 4/16. Вероятность выпадения четырех решек — 1/16.
Всего мы построим пять классов шириной один. Эти классы соответствуют количеству возможных голов: ноль, один, два, три или четыре. Над каждым классом рисуем вертикальную полосу или прямоугольник.Высота этих столбцов соответствует вероятностям, упомянутым в нашем вероятностном эксперименте подбрасывания четырех монет и подсчета орлов.
Гистограммы и вероятности
Приведенный выше пример не только демонстрирует построение гистограммы, но также показывает, что дискретные распределения вероятностей могут быть представлены с помощью гистограммы. Действительно, и дискретное распределение вероятностей можно представить гистограммой.
Чтобы построить гистограмму, представляющую распределение вероятностей, мы начинаем с выбора классов.Это должны быть результаты вероятностного эксперимента. Ширина каждого из этих классов должна составлять одну единицу. Высота столбцов гистограммы — это вероятности для каждого из результатов. Если гистограмма построена таким образом, площади столбцов также являются вероятностями.

Поскольку такая гистограмма дает нам вероятности, она зависит от нескольких условий. Одно из условий состоит в том, что только неотрицательные числа могут использоваться для шкалы, которая дает нам высоту данного столбца гистограммы.Второе условие состоит в том, что, поскольку вероятность равна площади, сумма всех площадей столбцов должна составлять единицу, что эквивалентно 100%.
Гистограммы и другие приложения
Столбцы на гистограмме не обязательно должны быть вероятностями. Гистограммы полезны не только в вероятностных областях, но и в других областях. Каждый раз, когда мы хотим сравнить частоту появления количественных данных, можно использовать гистограмму для отображения нашего набора данных.
гистограмм — обзор | Темы ScienceDirect
2.3.1 Нечеткая логика в низкоуровневом слиянии функций
Методы нечеткой гистограммы для IR не сильно отличаются от методов простых гистограмм. Единственное отличие состоит в том, что нечеткие гистограммы учитывают неопределенность рассматриваемых признаков (цвет, текстура, форма).
Самый простой подход к созданию нечеткой гистограммы — это нормализовать гистограмму по значению ее наибольшего интервала таким образом, чтобы наиболее вероятный цвет имел степень принадлежности 1 в нечетком множестве «изображения». Следовательно, наиболее вероятный цвет будет иметь степень принадлежности 1 в нечетком множестве «изображение». преобладающий цвет можно считать наиболее типичным для данного изображения, а типичность цвета в изображении измеряется построенной нечеткой гистограммой следующим образом:
(16) h2 (c) = h (c) maxc∈℘ h (c), ∀c∈℘,
где ℘ — набор цветов.
Подход нечеткой гистограммы основан на том принципе, что любой заданный цвет является неопределенным, поскольку фактически он может быть недопустимой версией другого цвета. Таким образом, пиксель заданного цвета будет вносить вклад не только в свой конкретный интервал, но также и в количество интервалов соседних интервалов на гистограмме.

Тико и др. . (2000) предложили метод создания цветовой гистограммы, основанный исключительно на компоненте оттенка в области хроматического изображения и на компоненте интенсивности в ахроматической области, которые взвешиваются в соответствии с их релевантностью в каждом пикселе изображения.Актуальность определяется с помощью нечеткого набора, который определяется SD тристимулов RGB. Формально это выражается двумя субунитарными весовыми значениями, связанными с каждым пикселем из компонентов оттенка и интенсивности из цветового пространства цветового тона-насыщенности-интенсивности (HSI). Значения веса определяются на основе значения SD в этом пикселе с помощью функции принадлежности и затем используются для создания взвешенных гистограмм компонентов оттенка и интенсивности.
ИК-система под названием FIRST (Fuzzy Image Retrieval SysTem) была представлена Кришнапурамом и др. .(2004). FIRST использует нечеткие реляционные графы с атрибутами (FARG) для представления изображений, где каждый узел в графе представляет область изображения, а каждое ребро представляет связь между двумя областями. Данный запрос преобразуется в FARG, и алгоритм сопоставления нечетких графов низкой сложности используется для сравнения графа запроса с FARG в базе данных. Использование схемы индексации, основанной на алгоритме кластеризации лидеров, позволяет избежать исчерпывающего поиска в базе данных FARG.
Классический метод создания цветовой гистограммы приводит к очень большим гистограммам с большими вариациями между соседними интервалами.Таким образом, небольшие изменения в изображении могут привести к большим изменениям гистограммы. Более того, тот факт, что каждое цветовое пространство состоит из трех компонентов, приводит к трехмерным гистограммам. Обработка и сравнение трехмерных гистограмм — сложная и дорогостоящая процедура. Следовательно, необходимость свести три измерения к одному может привести к эффективным подходам. Эта процедура проецирования трехмерной гистограммы на одну одномерную гистограмму называется гистограммой , связывающей .
 В качестве расширения этого понятия Konstantinidis et al .(2005) представили новый метод нечеткой связи для создания цветовой гистограммы на основе цветового пространства L * a * b *, который обеспечивает гистограмму, содержащую только 10 интервалов. Три компонента L * a * b * рассматривались как нечеткие множества, и предлагаемая гистограмма была получена путем связывания этих нечетких множеств и их дефаззификации с использованием соответствующих правил «если-то» в 10 основных цветов. Наличие в качестве дескриптора гистограммы с 10 ячейками может иметь множество применений. Одна такая гистограмма была предложена Котуласом и др. . (2006) в новом одноранговом приложении IR, в котором компактная нечеткая гистограмма использовалась для быстрой маршрутизации запроса к соответствующему одноранговому узлу.
В качестве расширения этого понятия Konstantinidis et al .(2005) представили новый метод нечеткой связи для создания цветовой гистограммы на основе цветового пространства L * a * b *, который обеспечивает гистограмму, содержащую только 10 интервалов. Три компонента L * a * b * рассматривались как нечеткие множества, и предлагаемая гистограмма была получена путем связывания этих нечетких множеств и их дефаззификации с использованием соответствующих правил «если-то» в 10 основных цветов. Наличие в качестве дескриптора гистограммы с 10 ячейками может иметь множество применений. Одна такая гистограмма была предложена Котуласом и др. . (2006) в новом одноранговом приложении IR, в котором компактная нечеткая гистограмма использовалась для быстрой маршрутизации запроса к соответствующему одноранговому узлу.В Nachtegael et al , 2007. предложено расширение метода нечеткой связи, в котором использовалось цветовое пространство HSI. Они разделили компоненты оттенка и интенсивности на нечеткие наборы и создали гистограмму из каждого набора. Во-первых, они вычислили степени принадлежности всех пикселей в каждом изображении по отношению к основным цветам, представленным нечеткими наборами. Таким образом они получили восемь новых «изображений», из которых они извлекли соответствующую нормализованную гистограмму, представляющую частотное распределение степеней принадлежности по отношению к восьми основным цветам.Затем они вычислили сходство каждой гистограммы из изображения запроса с изображениями в базе данных, объединив результаты в одно общее значение сходства для компонента оттенка, используя стандартное среднее значение в качестве оператора агрегирования. Как можно понять, этот процесс требует значительных затрат времени и вычислительных ресурсов, поскольку он включает в себя 16 различных гистограмм для каждого изображения в базе данных, и все они должны быть соответственно сравнены с изображением запроса.
Банерджи и Кунду (2006) предложили региональный подход для IR.
 Они разработали алгоритм, который может сегментировать изображение на нечеткие области на основе коэффициентов многомасштабного преобразования вейвлет-пакета. Функции на основе вейвлетов группируются с использованием алгоритма нечетких C-средних. Конечные центроиды кластера, которые являются репрезентативными точками, обозначают свойства цвета и текстуры заранее заданного количества классов. Нечеткие топологические отношения вычисляются из окончательной нечеткой матрицы разбиения. Свойства цвета и текстуры, обозначенные центроидами и пространственными отношениями между сегментированными областями, используются вместе, чтобы обеспечить окончательный дескриптор изображения.
Они разработали алгоритм, который может сегментировать изображение на нечеткие области на основе коэффициентов многомасштабного преобразования вейвлет-пакета. Функции на основе вейвлетов группируются с использованием алгоритма нечетких C-средних. Конечные центроиды кластера, которые являются репрезентативными точками, обозначают свойства цвета и текстуры заранее заданного количества классов. Нечеткие топологические отношения вычисляются из окончательной нечеткой матрицы разбиения. Свойства цвета и текстуры, обозначенные центроидами и пространственными отношениями между сегментированными областями, используются вместе, чтобы обеспечить окончательный дескриптор изображения.В подходе, в котором нечеткость вводится после извлечения дескрипторов, Simou et al . (2008) предлагают методологию семантического индексирования и поиска изображений, основанную на методах сегментации и классификации изображений в сочетании с нечеткими рассуждениями. В этой архитектуре анализа, основанного на знаниях, алгоритм сегментации сначала генерирует набор сверхсегментированных регионов. После этого используется процесс классификации регионов для присвоения семантических меток с использованием степени достоверности и одновременного объединения регионов на основе их семантического сходства.Эта информация представляет собой предполагаемый компонент нечеткой базы знаний, которая используется для уточнения ошибочно классифицированных регионов, а также для извлечения обширных неявных знаний, используемых для глобальной классификации изображений. Эти знания об изображениях хранятся в семантическом репозитории, разрешающем IR и ранжирование.
В работе Chatzichristofis and Boutalis (2008) был предложен новый дескриптор низкого уровня, который включал информацию о цвете и текстуре в одну нечетко квантованную гистограмму. Дескриптор является результатом комбинации трех нечетких единиц.Первоначально изображение сегментируется на заданное количество блоков, и каждый блок последовательно проходит через все нечеткие блоки.
 В первом блоке набор нечетких правил выполняет извлечение нечеткой гистограммы связывания (Konstantinidis et al ., 2005) из цветового пространства HSV, где каждая ячейка соответствует заданному цвету. В качестве второго модуля они предлагают нечеткую систему с двумя входами для расширения гистограммы с 10 ячейками в гистограмму с 24 ячейками, таким образом импортируя информацию, относящуюся к оттенку каждого представленного цвета.Затем, в третьем модуле, каждый блок изображения преобразуется с помощью вейвлет-преобразования Хаара и экспортируется набор элементов текстуры. Эти элементы используются в качестве входных данных в третьем нечетком блоке, который преобразует гистограмму с 24 ячейками в гистограмму с 192 ячейками, импортируя информацию о текстуре в предлагаемую функцию.
В первом блоке набор нечетких правил выполняет извлечение нечеткой гистограммы связывания (Konstantinidis et al ., 2005) из цветового пространства HSV, где каждая ячейка соответствует заданному цвету. В качестве второго модуля они предлагают нечеткую систему с двумя входами для расширения гистограммы с 10 ячейками в гистограмму с 24 ячейками, таким образом импортируя информацию, относящуюся к оттенку каждого представленного цвета.Затем, в третьем модуле, каждый блок изображения преобразуется с помощью вейвлет-преобразования Хаара и экспортируется набор элементов текстуры. Эти элементы используются в качестве входных данных в третьем нечетком блоке, который преобразует гистограмму с 24 ячейками в гистограмму с 192 ячейками, импортируя информацию о текстуре в предлагаемую функцию.Абулмагд и др. . (2009) также используют FARG для представления изображений, но в этом случае они внесли изменения в представление признаков изображения, так что оно использует концепции нечеткого множества и нечеткой логики для выражения среднего уровня содержания изображения.В своем исследовании они пытаются проверить, как нечеткая логика помогает сократить разрыв между низкоуровневыми функциями и концепциями высокого уровня и можно ли использовать ее для моделирования объектов изображения, их атрибутов и пространственных отношений. Они также предлагают алгоритм сопоставления графов, который имитирует образ мышления людей при сравнении изображений.
Расширение понятия реляционных графов, Филипп-Фолиге и др. . (2009) предложили алгоритм нечеткой сегментации, который выполняет рост области на изображении с помощью градиентных норм и строит функцию принадлежности, равную длине кратчайшего пути вдоль градиентного изображения к сердцевине области.Он объединяет преимущества как области, так и подхода к краю сегментации изображения, таким образом обеспечивая закрытые области и выполняя полную сегментацию изображения, которая ограничена большими значениями градиента.

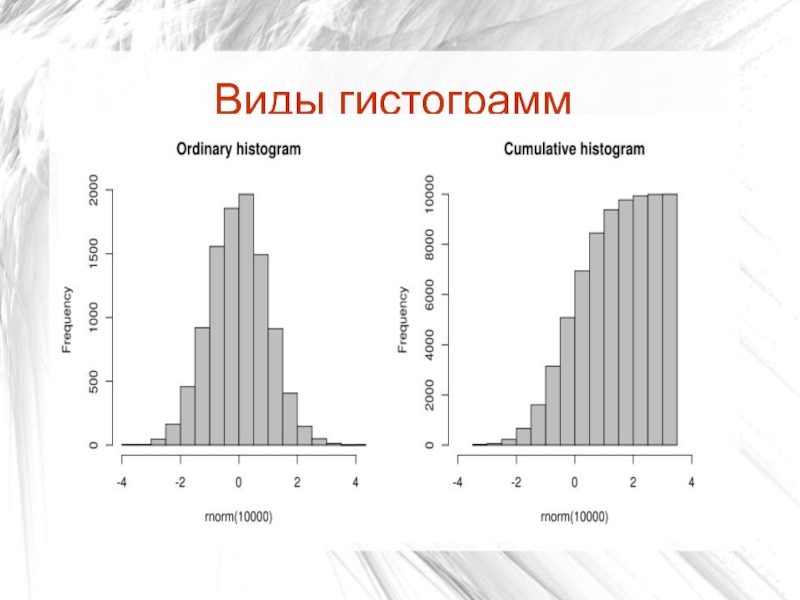
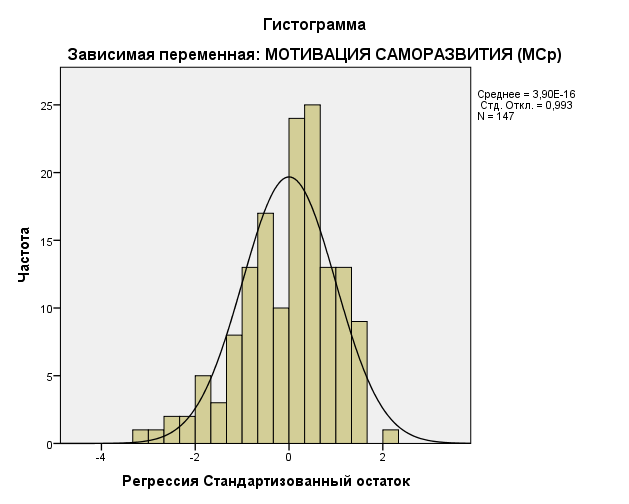 Подходит для непрерывных данных, таких как уклон, расстояние от водотоков и высота над уровнем моря.
Подходит для непрерывных данных, таких как уклон, расстояние от водотоков и высота над уровнем моря.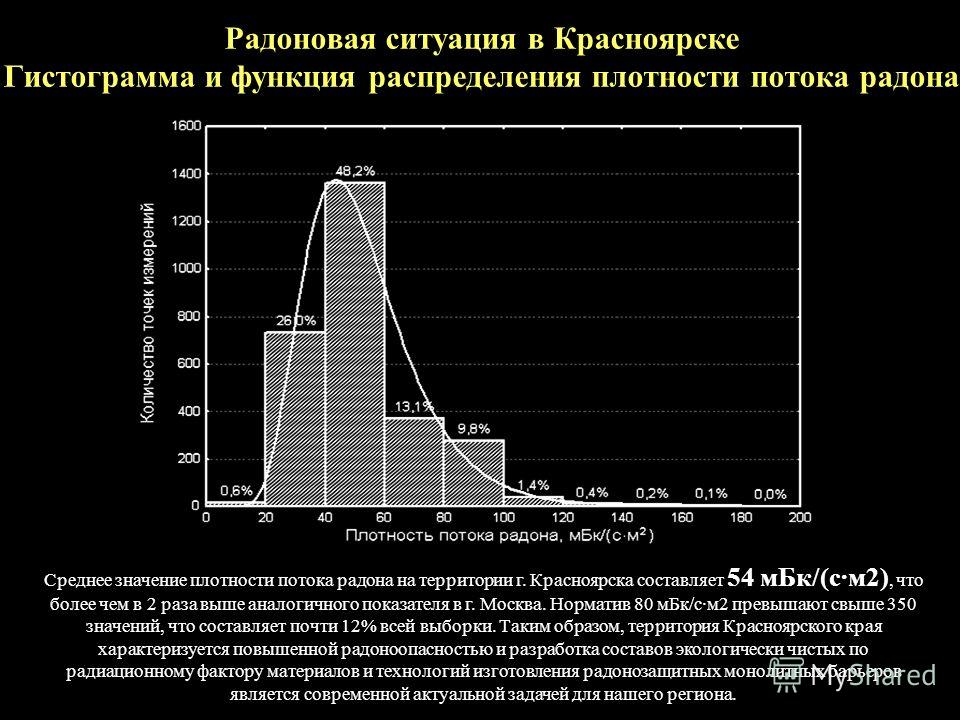 38. В более реальных числах тональный диапазон варьируется от черного до очень тусклого звездного света (0,00001 ), через внутреннее освещение (1-10), через освещенную солнцем улицу (1 000 000), до яркости самого солнца (100 000 000) и далеко за ее пределами. Все эти значения могут быть представлены в одном HDR-изображении.)
38. В более реальных числах тональный диапазон варьируется от черного до очень тусклого звездного света (0,00001 ), через внутреннее освещение (1-10), через освещенную солнцем улицу (1 000 000), до яркости самого солнца (100 000 000) и далеко за ее пределами. Все эти значения могут быть представлены в одном HDR-изображении.)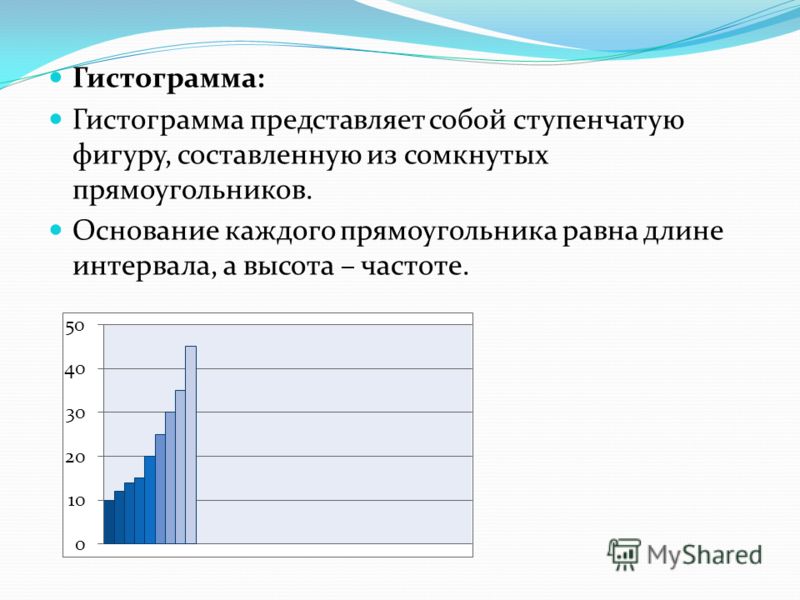
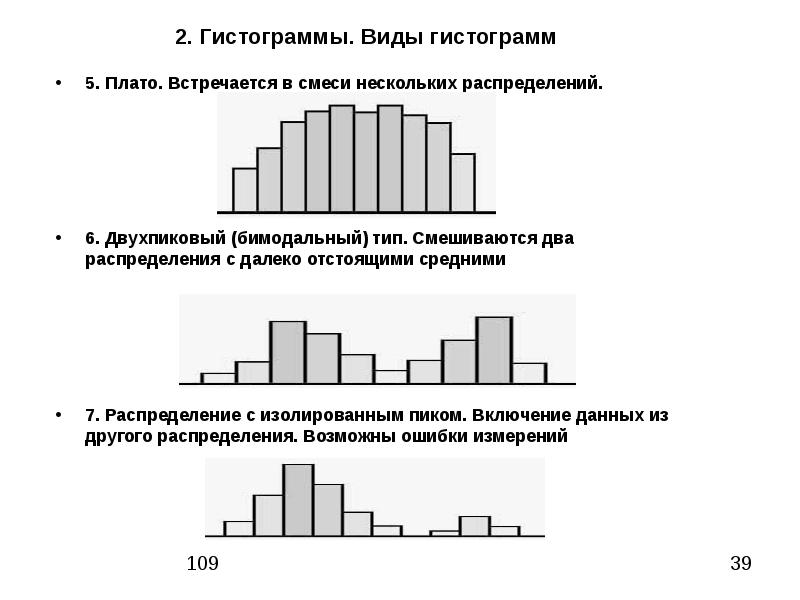 Преимущество этого метода заключается в том, что он позволяет фиксировать детали, которые в противном случае были бы потеряны, без необходимости прибегать к фильтрам градуировки ND или другим более экстремальным мерам.
Преимущество этого метода заключается в том, что он позволяет фиксировать детали, которые в противном случае были бы потеряны, без необходимости прибегать к фильтрам градуировки ND или другим более экстремальным мерам. ;
г) диаграмма, в которой отдельные значения представлены
полосами различной длины, расположенными горизонтально вдоль
оси Х.
6. Круговая диаграмма — это:
а) диаграмма, представленная в виде круга разбитого на секторы,
и в которой допускается только один ряд данных;
б) диаграмма, отдельные значения которой представлены точками
в декартовой системе координат;
в) диаграмма, в которой отдельные ряды данных представлены в
виде закрашенных разными цветами областей;
г) диаграмма, в которой используется система координат с тремя
координатными осями, что позволяет получить эффект
пространственного представления рядов данных.
7. Диаграмма, отдельные значения которой представлены точками в
декартовой системе координат, называется:
а) линейчатой;
б) точечной;
в) круговой;
г) гистограммой.
8. Гистограмма наиболее пригодна для: а) для отображения распределений;
б) сравнения различных членов группы;
в) для отображения динамики изменения данных;
3
;
г) диаграмма, в которой отдельные значения представлены
полосами различной длины, расположенными горизонтально вдоль
оси Х.
6. Круговая диаграмма — это:
а) диаграмма, представленная в виде круга разбитого на секторы,
и в которой допускается только один ряд данных;
б) диаграмма, отдельные значения которой представлены точками
в декартовой системе координат;
в) диаграмма, в которой отдельные ряды данных представлены в
виде закрашенных разными цветами областей;
г) диаграмма, в которой используется система координат с тремя
координатными осями, что позволяет получить эффект
пространственного представления рядов данных.
7. Диаграмма, отдельные значения которой представлены точками в
декартовой системе координат, называется:
а) линейчатой;
б) точечной;
в) круговой;
г) гистограммой.
8. Гистограмма наиболее пригодна для: а) для отображения распределений;
б) сравнения различных членов группы;
в) для отображения динамики изменения данных;
3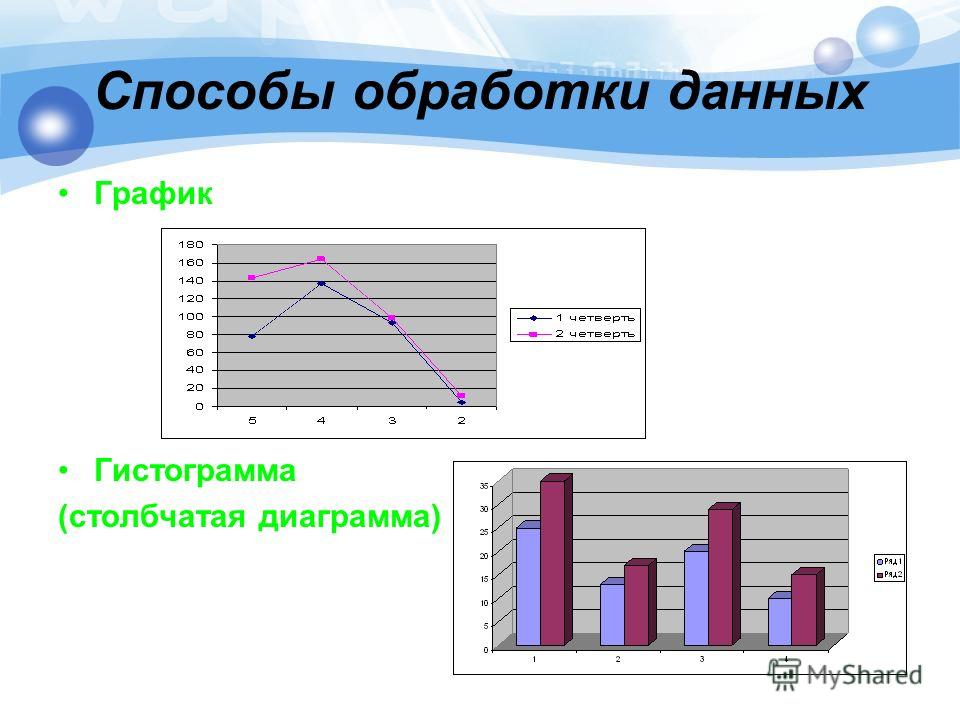 Excel-это:
Excel-это: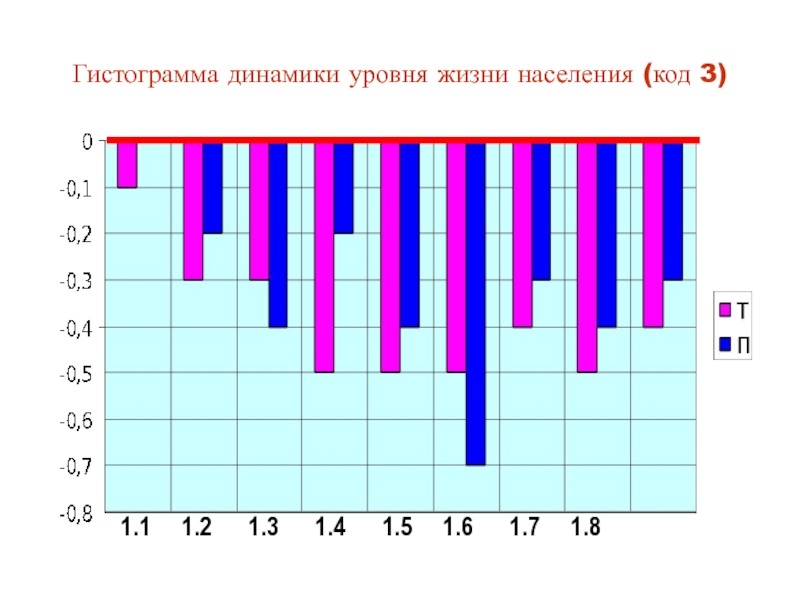 В электронных
таблицах со знака «=» начинается
ввод
В электронных
таблицах со знака «=» начинается
ввод
 Это говорит о том, что прогресс в области информационных технологий приводит к расширению сферы их применения и, соответственно, к востребованности специалистов, владеющих современными технологиями обработки и анализа данных. Таким образом возникает необходимость подготовки учителей, владеющих знаниями и методикой обучения построения динамических диаграмм и, соответственно, корректировки и обновления содержания курса информатики в высшей школе.
Это говорит о том, что прогресс в области информационных технологий приводит к расширению сферы их применения и, соответственно, к востребованности специалистов, владеющих современными технологиями обработки и анализа данных. Таким образом возникает необходимость подготовки учителей, владеющих знаниями и методикой обучения построения динамических диаграмм и, соответственно, корректировки и обновления содержания курса информатики в высшей школе. Методические разработки по изучению данной темы в курсе информатики в сети не представлены.
Методические разработки по изучению данной темы в курсе информатики в сети не представлены.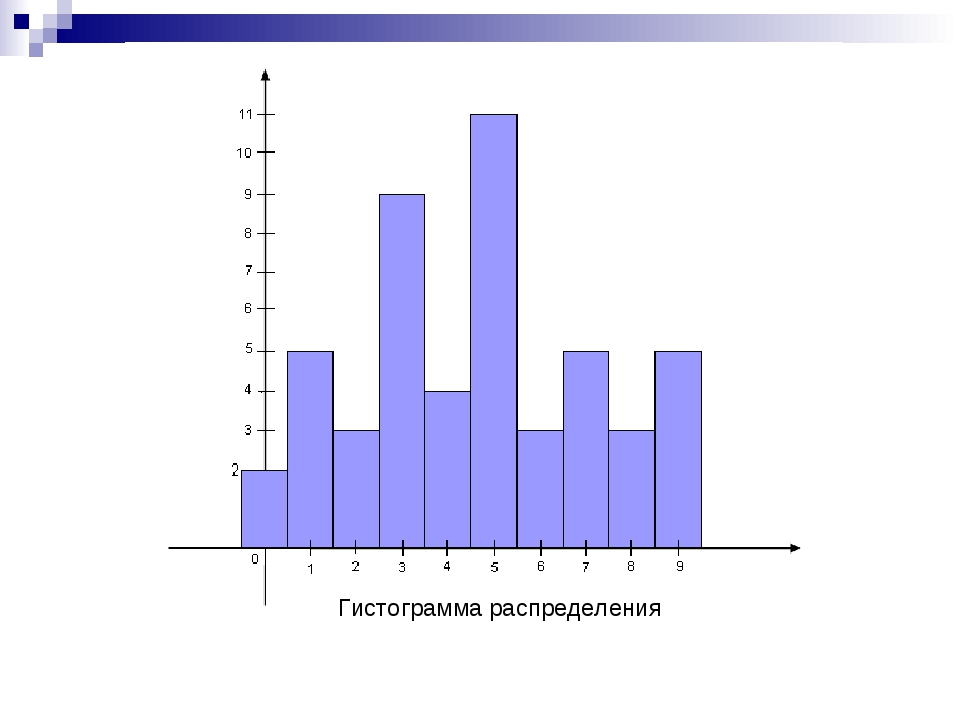 Кроме того, графическое изображение позволяет осуществить контроль достоверности полученных данных, так как на графике достаточно ярко проявляются возможные неточности, которые могут быть связаны с ошибками на каком-либо этапе проведения исследования.
Кроме того, графическое изображение позволяет осуществить контроль достоверности полученных данных, так как на графике достаточно ярко проявляются возможные неточности, которые могут быть связаны с ошибками на каком-либо этапе проведения исследования. Спрос вызывает предложение. В сети появились описания креативных решений задач по визуализации больших массивов данных экономической статистики с помощью обычных диаграмм Excel, которые обладают свойством подвижности, изменяемости. Возникло и общее название для них — динамические диаграммы. Динамическая — означает меняющаяся, движущаяся, отображающая разные диапазоны большого массива данных в зависимости от настроек пользователя. Динамическая диаграмма интерактивна, содержит элементы управления для выбора и уточнения диапазонов отображения данных.
Спрос вызывает предложение. В сети появились описания креативных решений задач по визуализации больших массивов данных экономической статистики с помощью обычных диаграмм Excel, которые обладают свойством подвижности, изменяемости. Возникло и общее название для них — динамические диаграммы. Динамическая — означает меняющаяся, движущаяся, отображающая разные диапазоны большого массива данных в зависимости от настроек пользователя. Динамическая диаграмма интерактивна, содержит элементы управления для выбора и уточнения диапазонов отображения данных.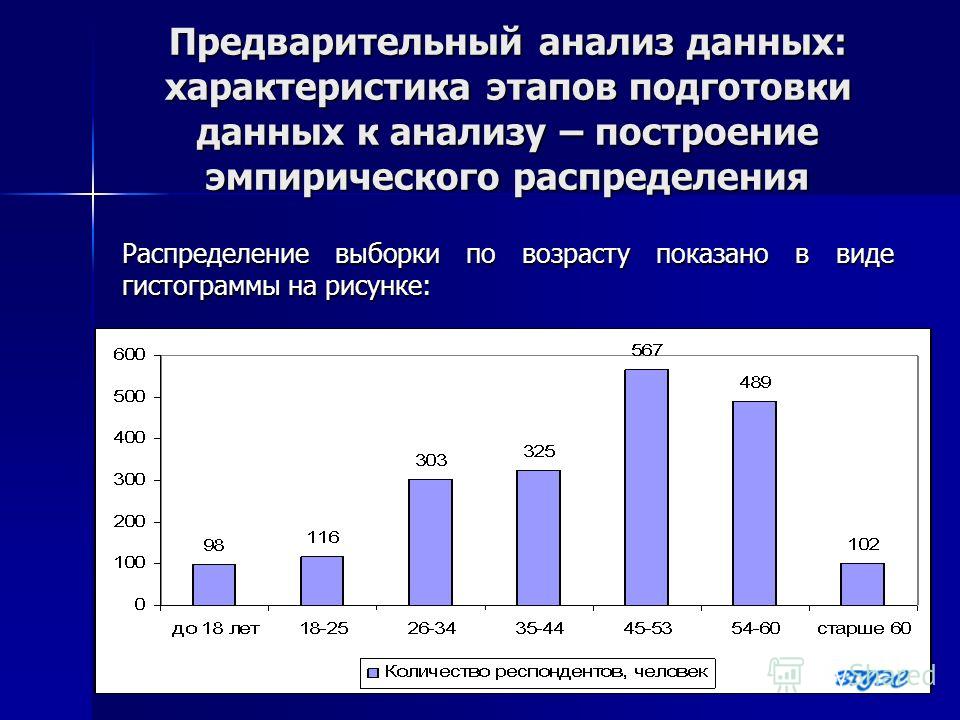
 ;К) задают диапазоны данных и подписей для выделенного ряда диаграммы: X — адрес ячейки с именем
;К) задают диапазоны данных и подписей для выделенного ряда диаграммы: X — адрес ячейки с именем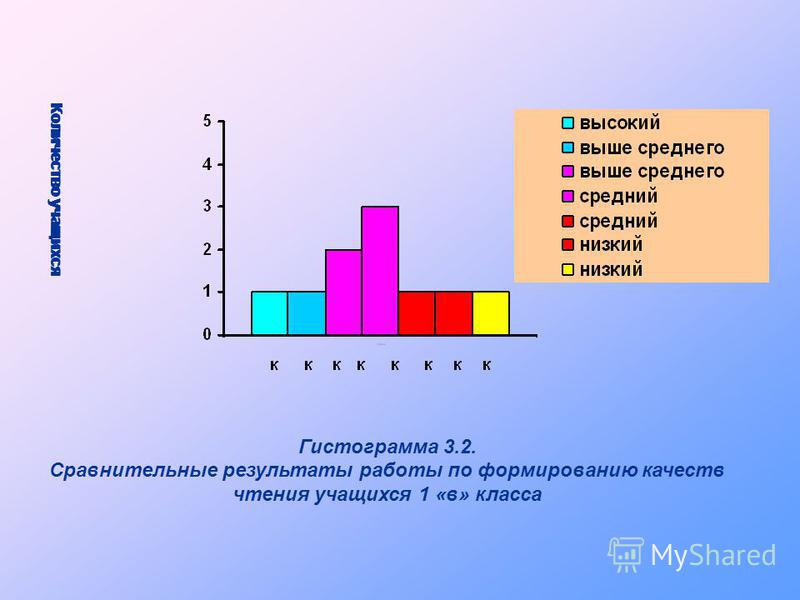 1б. Динамическая диаграмма при выбранном месяце «вересень»
1б. Динамическая диаграмма при выбранном месяце «вересень» 2а. Динамическая диаграмма изменения двух валют в диапазоне
2а. Динамическая диаграмма изменения двух валют в диапазоне Динамические диаграммы, которые являются результатом выполнения заданий, сами по себе настолько привлекательны и удивительны, что неизменно вызывают положительную мотивацию студентов в дальнейшем освоении современных информационных технологий. Результат обучения при этом объединяет в себе интеллектуальную и практическую составляющую образования.
Динамические диаграммы, которые являются результатом выполнения заданий, сами по себе настолько привлекательны и удивительны, что неизменно вызывают положительную мотивацию студентов в дальнейшем освоении современных информационных технологий. Результат обучения при этом объединяет в себе интеллектуальную и практическую составляющую образования. Описано загальні принципи і методи їх побудови у Excel. Запропоновано приклади для вивчення динамічних діаграм студентами фізико-математичного факультету на лабораторних заняттях з інформатики при вивчення табличного процесора Excel.
Описано загальні принципи і методи їх побудови у Excel. Запропоновано приклади для вивчення динамічних діаграм студентами фізико-математичного факультету на лабораторних заняттях з інформатики при вивчення табличного процесора Excel.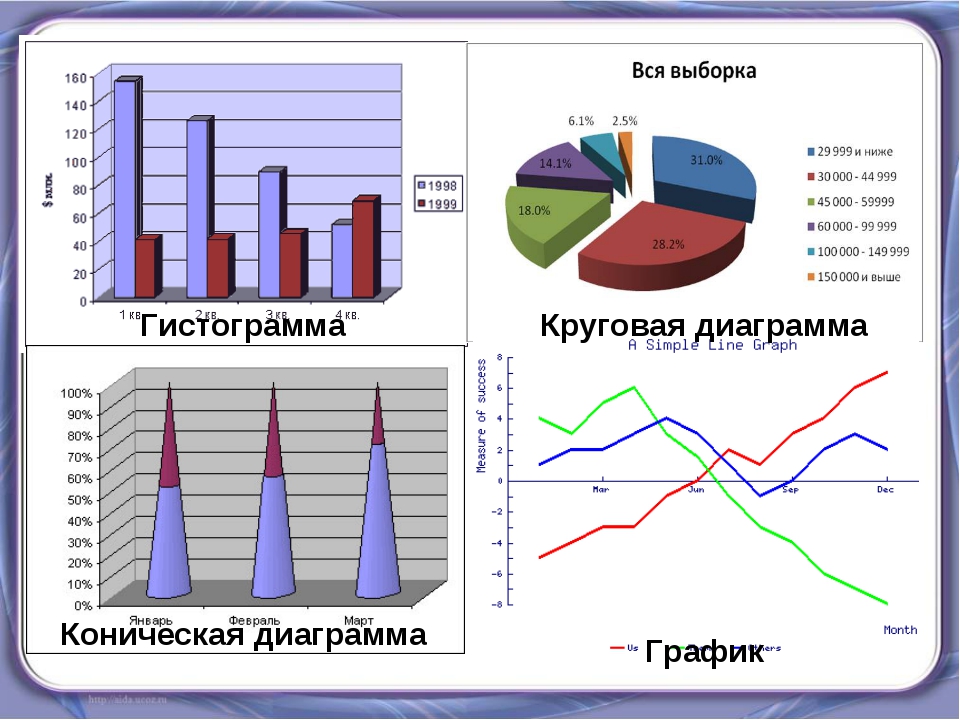
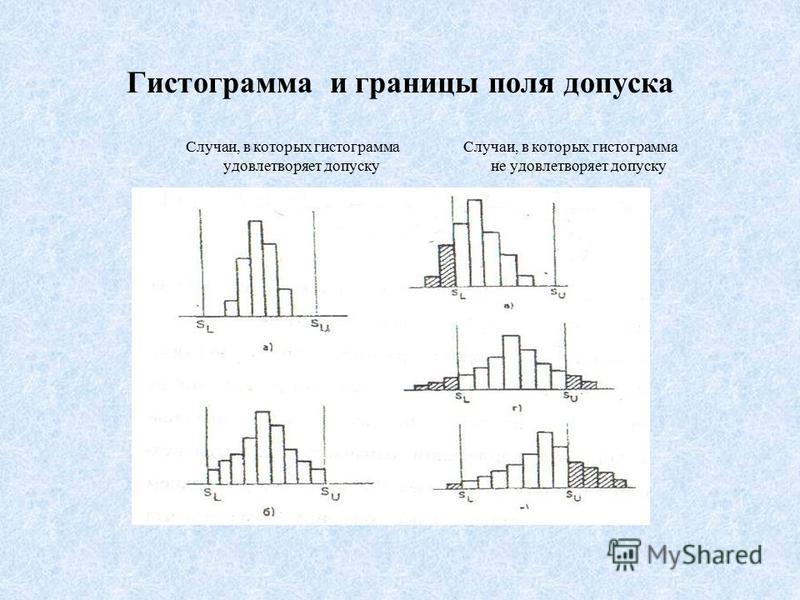 Гистограмма делит диапазон возможных значений в наборе данных на классы или группы. Для каждой группы создается прямоугольник с базовой длиной, равной диапазону значений в этой конкретной группе, и площадью, пропорциональной количеству наблюдений, попадающих в эту группу. Это означает, что прямоугольники будут нарисованы неодинаковой высоты. Гистограмма выглядит как вертикальная гистограмма, но когда переменные непрерывны, между столбцами нет промежутков.Однако, когда переменные дискретны, между полосами следует оставлять промежутки. Рисунок 1 — хороший пример гистограммы.
Гистограмма делит диапазон возможных значений в наборе данных на классы или группы. Для каждой группы создается прямоугольник с базовой длиной, равной диапазону значений в этой конкретной группе, и площадью, пропорциональной количеству наблюдений, попадающих в эту группу. Это означает, что прямоугольники будут нарисованы неодинаковой высоты. Гистограмма выглядит как вертикальная гистограмма, но когда переменные непрерывны, между столбцами нет промежутков.Однако, когда переменные дискретны, между полосами следует оставлять промежутки. Рисунок 1 — хороший пример гистограммы.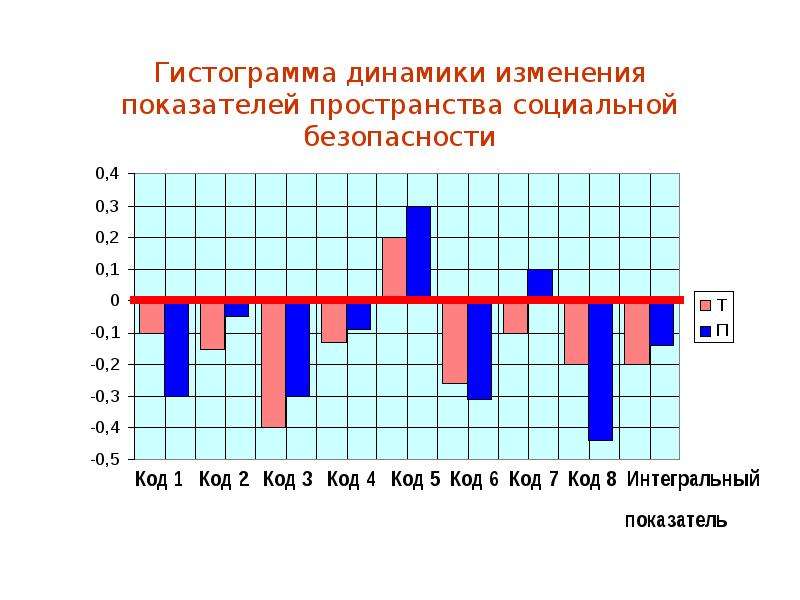
 В распределении со смещением влево большое количество значений данных находится в правой части, а меньшее количество значений данных — в левой. Распределение с перекосом вправо обычно возникает, когда данные имеют границу диапазона в правой части гистограммы. Например, граница, такая как 100.
В распределении со смещением влево большое количество значений данных находится в правой части, а меньшее количество значений данных — в левой. Распределение с перекосом вправо обычно возникает, когда данные имеют границу диапазона в правой части гистограммы. Например, граница, такая как 100.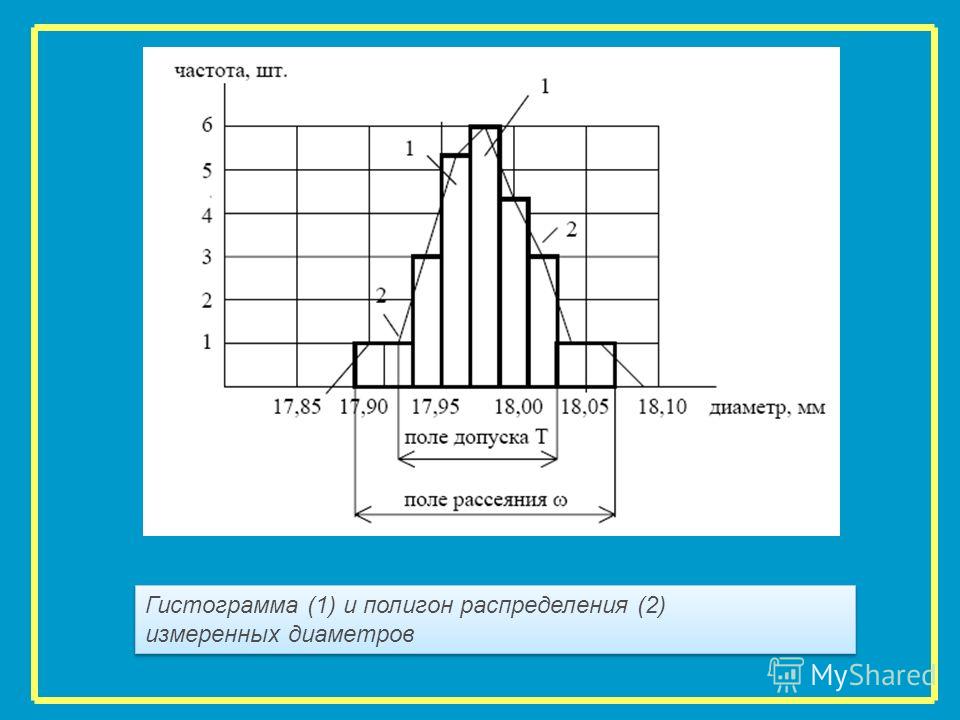
 Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения.
Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие сведения.
 Как правило, диаграммы передают информацию о наших данных быстрее, чем таблицы , хотя и менее точно.
Как правило, диаграммы передают информацию о наших данных быстрее, чем таблицы , хотя и менее точно.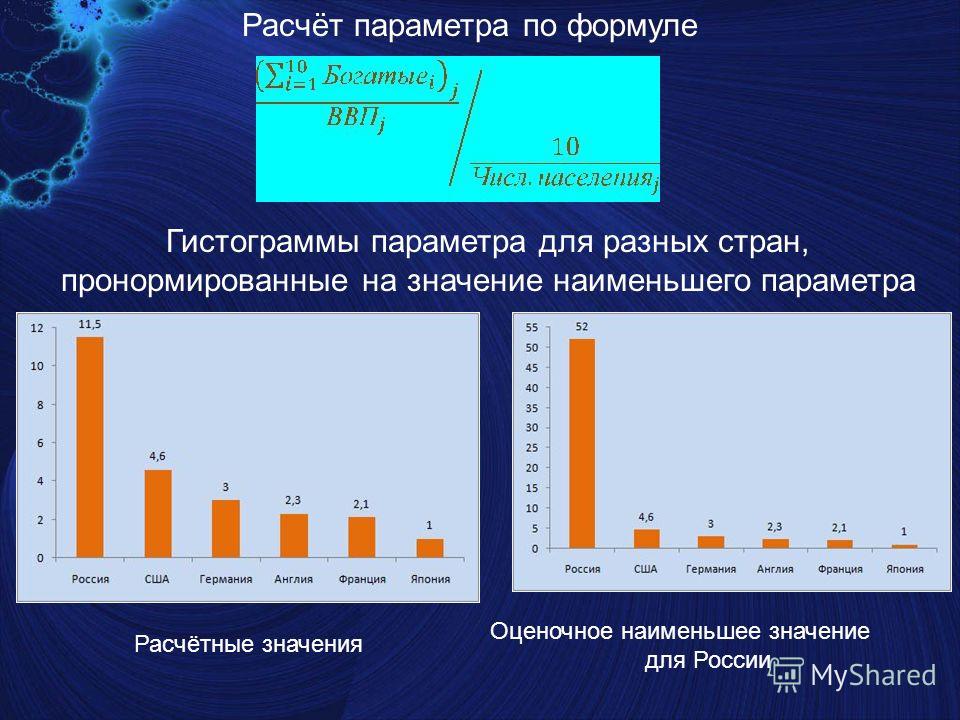 Если мы выберем процентное соотношение внутри групп уровня должностей, то каждая гистограмма будет иметь одинаковую площадь поверхности 100%. Результат показан ниже.
Если мы выберем процентное соотношение внутри групп уровня должностей, то каждая гистограмма будет иметь одинаковую площадь поверхности 100%. Результат показан ниже.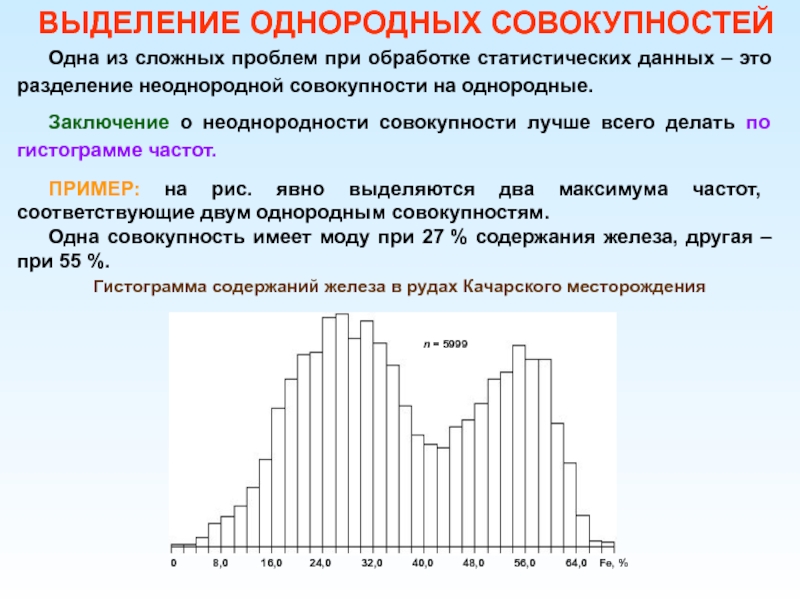 Как видите, гистограммы непрерывны и не имеют пропусков, однако, если для определенной точки нет значения частоты, могут возникать пропуски. Эти пробелы можно легко обнаружить и они служат еще одним преимуществом гистограммы.
Как видите, гистограммы непрерывны и не имеют пропусков, однако, если для определенной точки нет значения частоты, могут возникать пропуски. Эти пробелы можно легко обнаружить и они служат еще одним преимуществом гистограммы.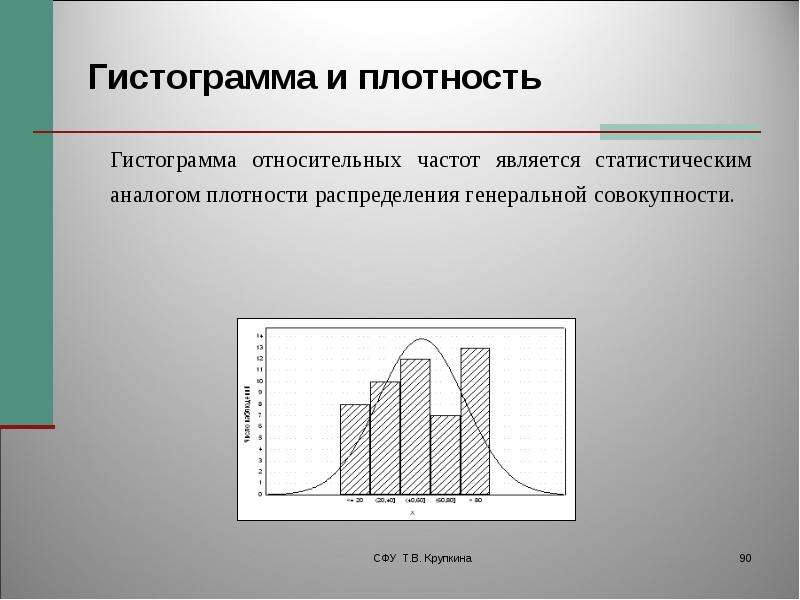 Это указывает на то, что данные собираются из двух разных систем. В случае возникновения такого распределения данные должны быть проанализированы отдельно для обоих пиков.
Это указывает на то, что данные собираются из двух разных систем. В случае возникновения такого распределения данные должны быть проанализированы отдельно для обоих пиков.
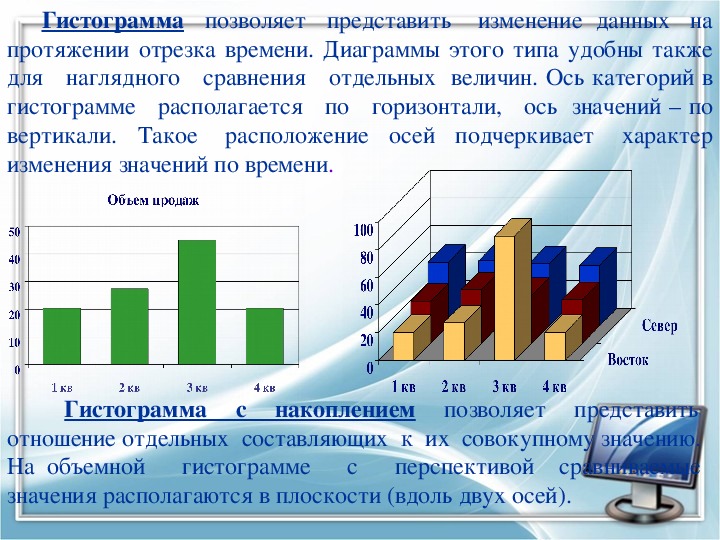 Каждая полоса обычно охватывает диапазон числовых значений, называемых ячейкой или классом; высота столбца указывает частоту точек данных со значением в соответствующем интервале.
Каждая полоса обычно охватывает диапазон числовых значений, называемых ячейкой или классом; высота столбца указывает частоту точек данных со значением в соответствующем интервале.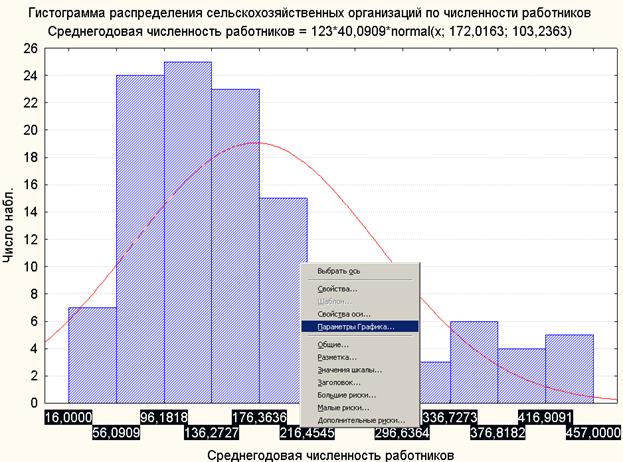 Какая сторона будет выбрана, зависит от инструмента визуализации; у некоторых инструментов есть возможность переопределить их настройки по умолчанию.В этой статье предполагается, что значения на границе ячейки будут присвоены ячейке справа.
Какая сторона будет выбрана, зависит от инструмента визуализации; у некоторых инструментов есть возможность переопределить их настройки по умолчанию.В этой статье предполагается, что значения на границе ячейки будут присвоены ячейке справа.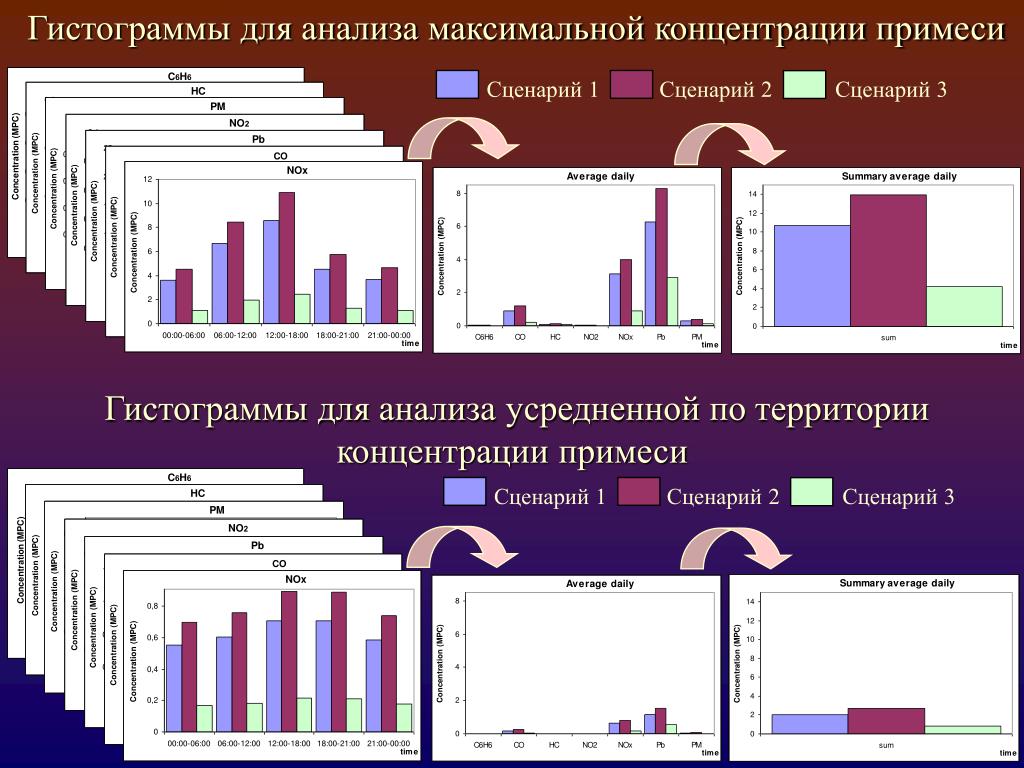 Чем больше размер ячеек, тем меньше ячеек будет для охвата всего диапазона данных. Чем меньше размер бункера, тем больше должно быть бункеров. Стоит потратить некоторое время на то, чтобы протестировать различные размеры бункеров, чтобы увидеть, как распределение выглядит в каждом из них, а затем выбрать график, который лучше всего представляет данные. Если у вас слишком много бинов, тогда распределение данных будет выглядеть грубым, и будет сложно отличить сигнал от шума.С другой стороны, при слишком малом количестве интервалов гистограмме будет не хватать деталей, необходимых для различения любого полезного паттерна из данных.
Чем больше размер ячеек, тем меньше ячеек будет для охвата всего диапазона данных. Чем меньше размер бункера, тем больше должно быть бункеров. Стоит потратить некоторое время на то, чтобы протестировать различные размеры бункеров, чтобы увидеть, как распределение выглядит в каждом из них, а затем выбрать график, который лучше всего представляет данные. Если у вас слишком много бинов, тогда распределение данных будет выглядеть грубым, и будет сложно отличить сигнал от шума.С другой стороны, при слишком малом количестве интервалов гистограмме будет не хватать деталей, необходимых для различения любого полезного паттерна из данных. Бин от 0 до 2,5 имеет возможность собирать три разных значения (0, 1, 2), но следующий интервал от 2,5 до 5 может собирать только два разных значения (3, 4-5 попадут в следующий интервал).Это означает, что ваша гистограмма может выглядеть неестественно «неровной» просто из-за количества значений, которые может принимать каждая ячейка.
Бин от 0 до 2,5 имеет возможность собирать три разных значения (0, 1, 2), но следующий интервал от 2,5 до 5 может собирать только два разных значения (3, 4-5 попадут в следующий интервал).Это означает, что ваша гистограмма может выглядеть неестественно «неровной» просто из-за количества значений, которые может принимать каждая ячейка.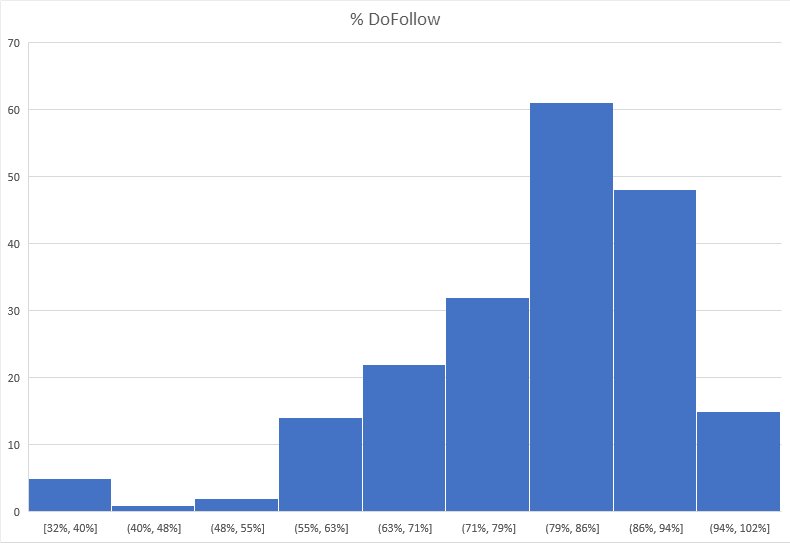 Например, если у вас есть ответы на опрос по шкале от 1 до 5, значения кодирования от «категорически не согласен» до «полностью согласен», то частотное распределение должно быть визуализировано в виде гистограммы. Причина в том, что различия между отдельными ценностями могут быть непоследовательными: мы действительно не знаем, что значимая разница между 1 и 2 («категорически не согласен» — «не согласен») такая же, как разница между 2 и 3. («Не согласен» — «ни согласен, ни не согласен»).
Например, если у вас есть ответы на опрос по шкале от 1 до 5, значения кодирования от «категорически не согласен» до «полностью согласен», то частотное распределение должно быть визуализировано в виде гистограммы. Причина в том, что различия между отдельными ценностями могут быть непоследовательными: мы действительно не знаем, что значимая разница между 1 и 2 («категорически не согласен» — «не согласен») такая же, как разница между 2 и 3. («Не согласен» — «ни согласен, ни не согласен»).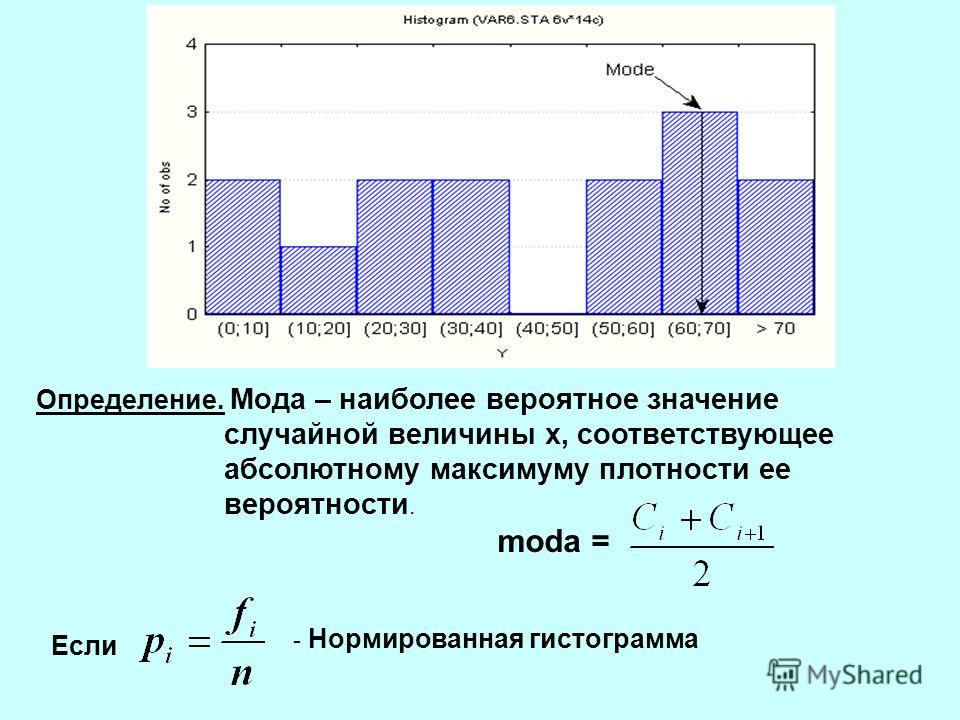 Когда размеры бункера совпадают, это делает измерение площади стержня и высоты эквивалентным. Однако в гистограмме с переменными размерами ячеек высота больше не может соответствовать общей частоте появления. Это исказит представление о том, сколько точек находится в каждой ячейке, поскольку увеличение размера ячейки только увеличивает ее размер.На центральном графике рисунка ниже интервалы 5-6, 6-7 и 7-10 выглядят так, как будто они содержат больше точек, чем на самом деле.
Когда размеры бункера совпадают, это делает измерение площади стержня и высоты эквивалентным. Однако в гистограмме с переменными размерами ячеек высота больше не может соответствовать общей частоте появления. Это исказит представление о том, сколько точек находится в каждой ячейке, поскольку увеличение размера ячейки только увеличивает ее размер.На центральном графике рисунка ниже интервалы 5-6, 6-7 и 7-10 выглядят так, как будто они содержат больше точек, чем на самом деле.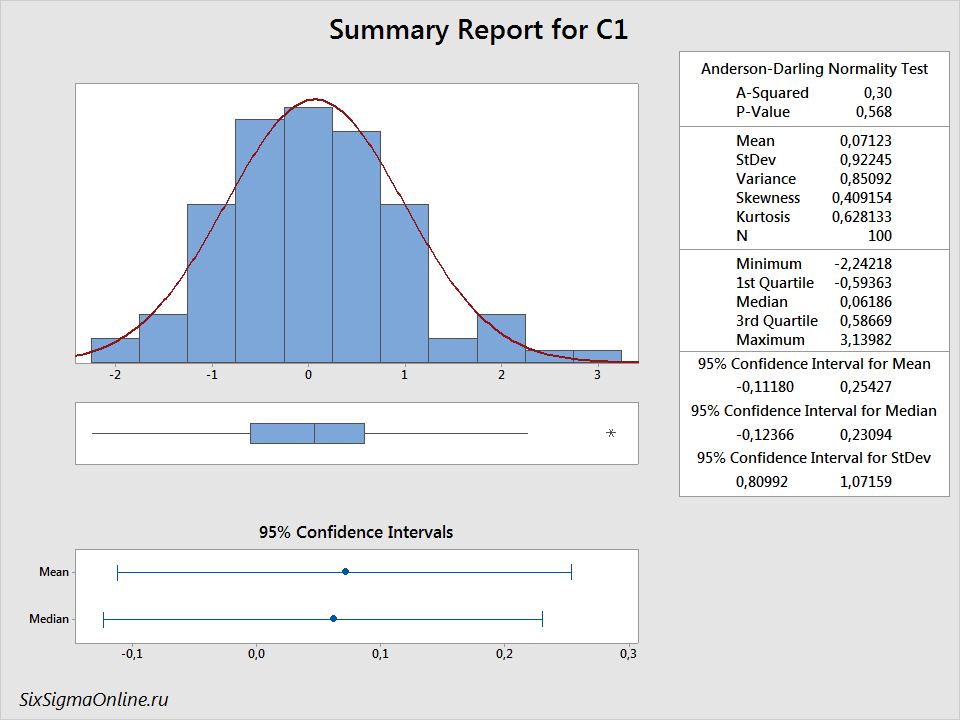 Абсолютная частота — это просто естественное количество появлений в каждом интервале, а относительная частота — это пропорция появлений в каждом интервале. Выбор единиц оси будет зависеть от того, какие виды сравнений вы хотите выделить при распределении данных.
Абсолютная частота — это просто естественное количество появлений в каждом интервале, а относительная частота — это пропорция появлений в каждом интервале. Выбор единиц оси будет зависеть от того, какие виды сравнений вы хотите выделить при распределении данных.

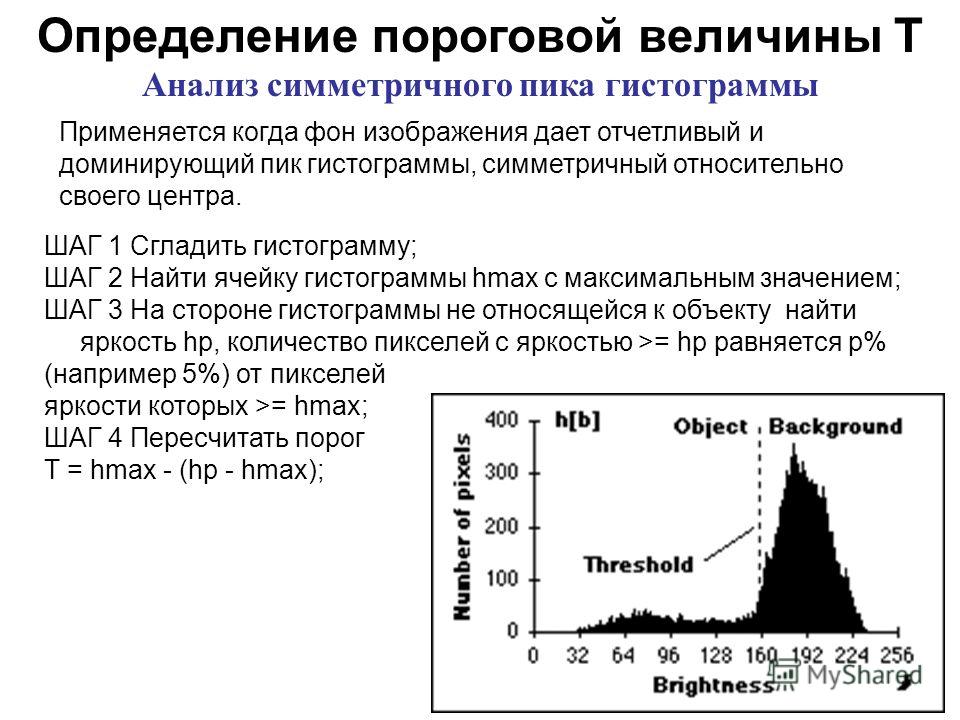 С другой стороны, гистограммы используются для данных, которые находятся, по крайней мере, на порядковом уровне измерения.Классы гистограммы — это диапазоны значений.
С другой стороны, гистограммы используются для данных, которые находятся, по крайней мере, на порядковом уровне измерения.Классы гистограммы — это диапазоны значений.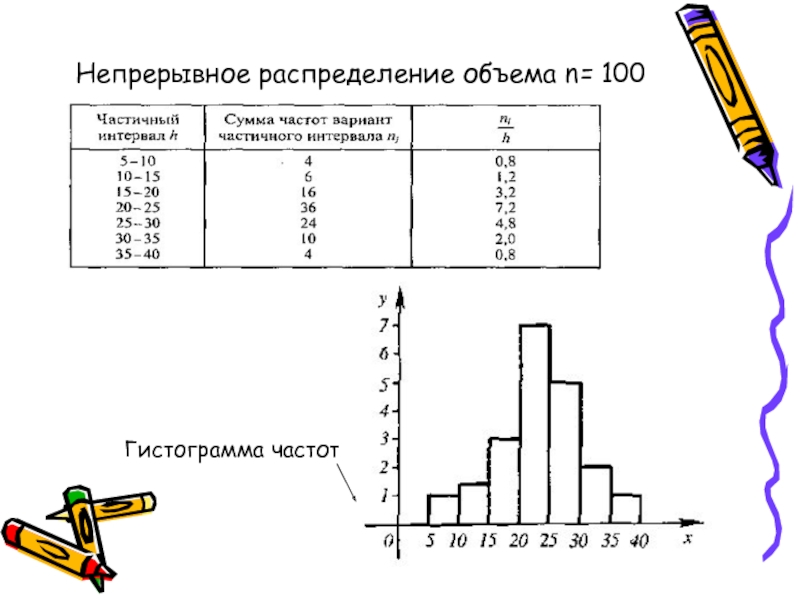
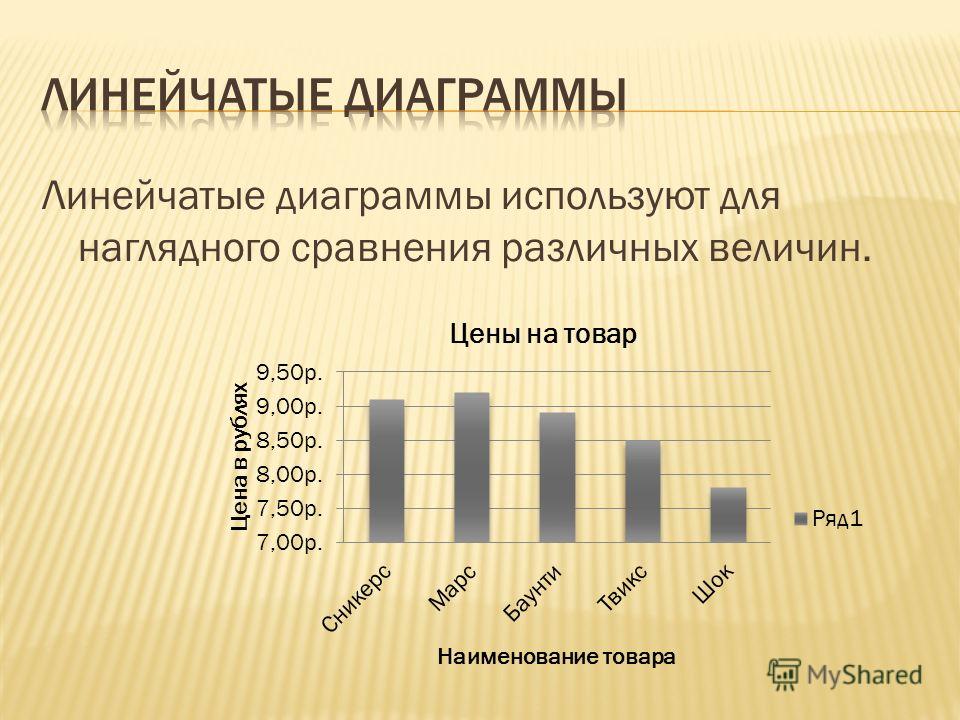
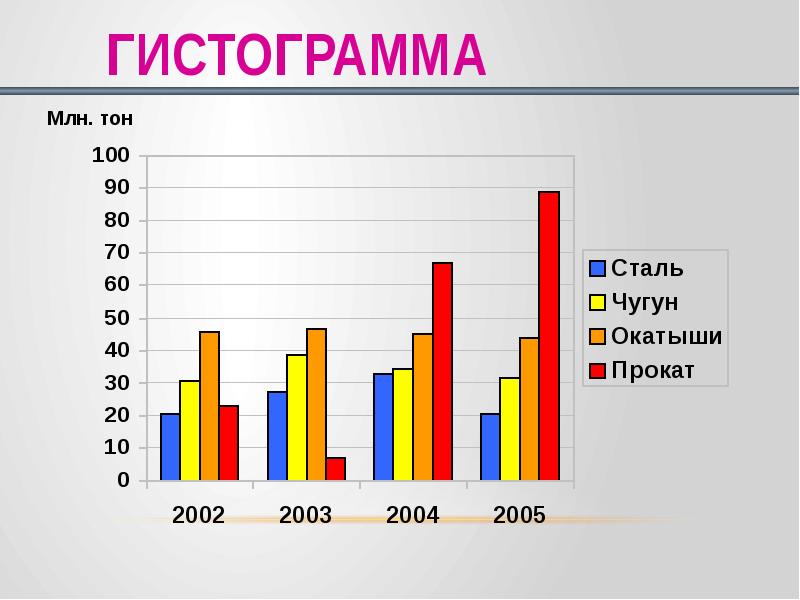 В качестве расширения этого понятия Konstantinidis et al .(2005) представили новый метод нечеткой связи для создания цветовой гистограммы на основе цветового пространства L * a * b *, который обеспечивает гистограмму, содержащую только 10 интервалов. Три компонента L * a * b * рассматривались как нечеткие множества, и предлагаемая гистограмма была получена путем связывания этих нечетких множеств и их дефаззификации с использованием соответствующих правил «если-то» в 10 основных цветов. Наличие в качестве дескриптора гистограммы с 10 ячейками может иметь множество применений. Одна такая гистограмма была предложена Котуласом и др. . (2006) в новом одноранговом приложении IR, в котором компактная нечеткая гистограмма использовалась для быстрой маршрутизации запроса к соответствующему одноранговому узлу.
В качестве расширения этого понятия Konstantinidis et al .(2005) представили новый метод нечеткой связи для создания цветовой гистограммы на основе цветового пространства L * a * b *, который обеспечивает гистограмму, содержащую только 10 интервалов. Три компонента L * a * b * рассматривались как нечеткие множества, и предлагаемая гистограмма была получена путем связывания этих нечетких множеств и их дефаззификации с использованием соответствующих правил «если-то» в 10 основных цветов. Наличие в качестве дескриптора гистограммы с 10 ячейками может иметь множество применений. Одна такая гистограмма была предложена Котуласом и др. . (2006) в новом одноранговом приложении IR, в котором компактная нечеткая гистограмма использовалась для быстрой маршрутизации запроса к соответствующему одноранговому узлу.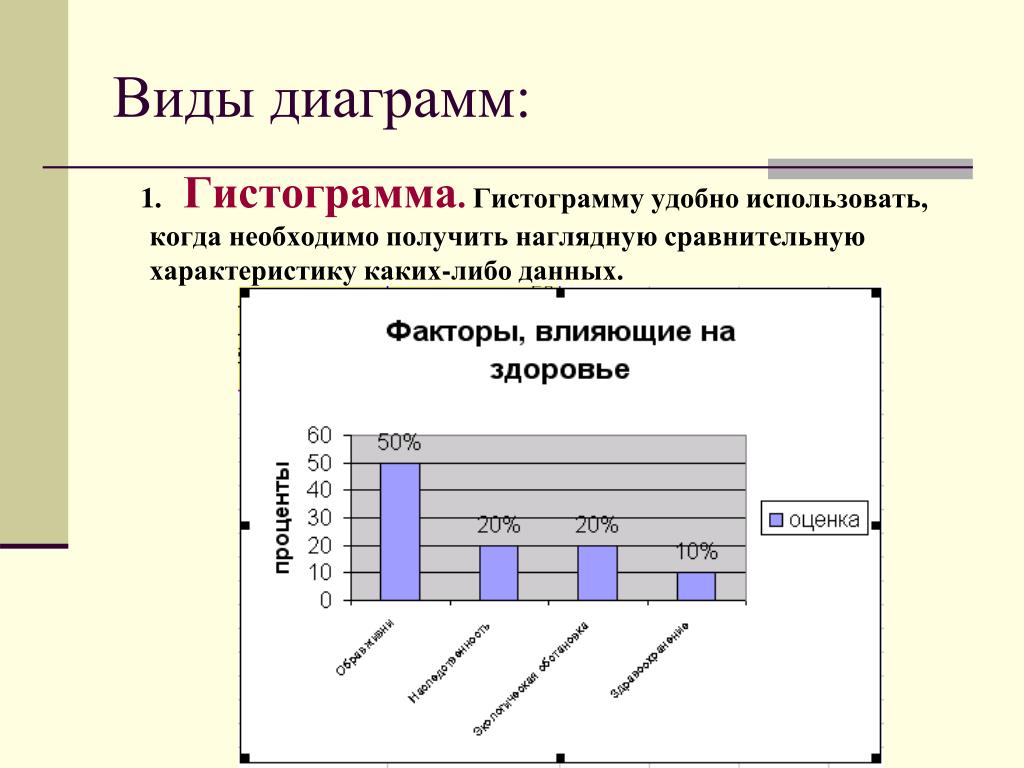 Они разработали алгоритм, который может сегментировать изображение на нечеткие области на основе коэффициентов многомасштабного преобразования вейвлет-пакета. Функции на основе вейвлетов группируются с использованием алгоритма нечетких C-средних. Конечные центроиды кластера, которые являются репрезентативными точками, обозначают свойства цвета и текстуры заранее заданного количества классов. Нечеткие топологические отношения вычисляются из окончательной нечеткой матрицы разбиения. Свойства цвета и текстуры, обозначенные центроидами и пространственными отношениями между сегментированными областями, используются вместе, чтобы обеспечить окончательный дескриптор изображения.
Они разработали алгоритм, который может сегментировать изображение на нечеткие области на основе коэффициентов многомасштабного преобразования вейвлет-пакета. Функции на основе вейвлетов группируются с использованием алгоритма нечетких C-средних. Конечные центроиды кластера, которые являются репрезентативными точками, обозначают свойства цвета и текстуры заранее заданного количества классов. Нечеткие топологические отношения вычисляются из окончательной нечеткой матрицы разбиения. Свойства цвета и текстуры, обозначенные центроидами и пространственными отношениями между сегментированными областями, используются вместе, чтобы обеспечить окончательный дескриптор изображения.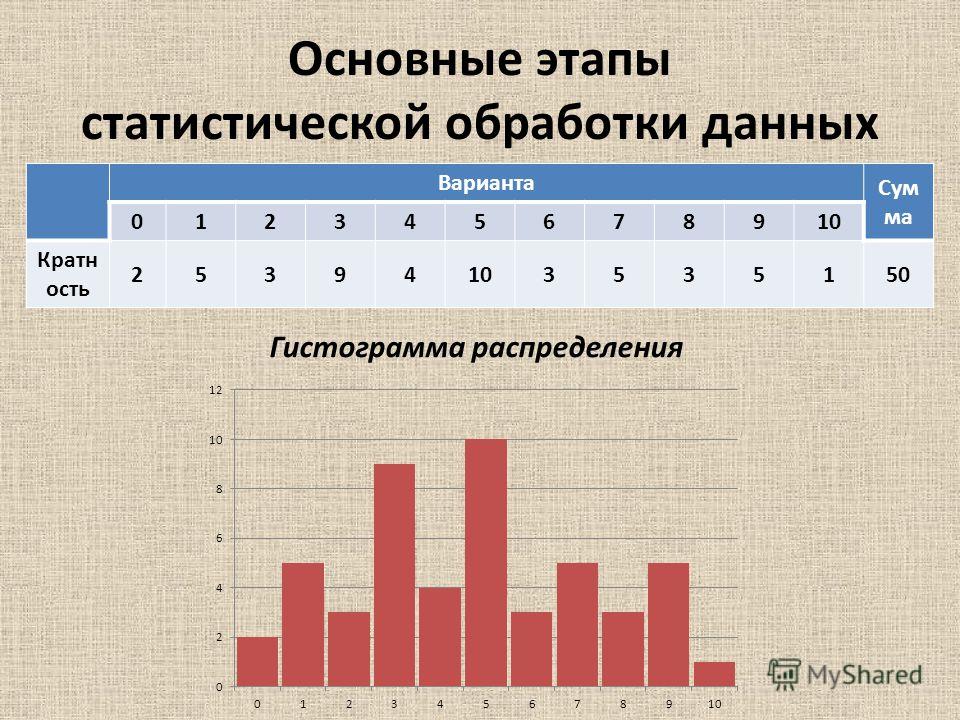 В первом блоке набор нечетких правил выполняет извлечение нечеткой гистограммы связывания (Konstantinidis et al ., 2005) из цветового пространства HSV, где каждая ячейка соответствует заданному цвету. В качестве второго модуля они предлагают нечеткую систему с двумя входами для расширения гистограммы с 10 ячейками в гистограмму с 24 ячейками, таким образом импортируя информацию, относящуюся к оттенку каждого представленного цвета.Затем, в третьем модуле, каждый блок изображения преобразуется с помощью вейвлет-преобразования Хаара и экспортируется набор элементов текстуры. Эти элементы используются в качестве входных данных в третьем нечетком блоке, который преобразует гистограмму с 24 ячейками в гистограмму с 192 ячейками, импортируя информацию о текстуре в предлагаемую функцию.
В первом блоке набор нечетких правил выполняет извлечение нечеткой гистограммы связывания (Konstantinidis et al ., 2005) из цветового пространства HSV, где каждая ячейка соответствует заданному цвету. В качестве второго модуля они предлагают нечеткую систему с двумя входами для расширения гистограммы с 10 ячейками в гистограмму с 24 ячейками, таким образом импортируя информацию, относящуюся к оттенку каждого представленного цвета.Затем, в третьем модуле, каждый блок изображения преобразуется с помощью вейвлет-преобразования Хаара и экспортируется набор элементов текстуры. Эти элементы используются в качестве входных данных в третьем нечетком блоке, который преобразует гистограмму с 24 ячейками в гистограмму с 192 ячейками, импортируя информацию о текстуре в предлагаемую функцию.